- СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
- СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
- Пример построения СДНФ для медианы
- Примеры СДНФ для некоторых функций
- Далее:
- Таблица истинности
- Правила ввода логической функции
- Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения
- Что такое СДНФ
- Что такое СКНФ
- Правила построения по таблице истинности
- Дизъюнктивная форма
- Конъюнктивная форма
- Алгоритм приведения к СДНФ и СКНФ
- Доказательство эквивалентности
- Поглощение
- Склеивание
- Обобщенное склеивание
- Расщепление
- Примеры с решением
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
- Услуги проектирования
- Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв]
- СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
- полная, если в неё каждая переменная < или её отрицание >входит ровно 1 раз;
- монотонная, если она не содержит отрицаний переменных.
ДНФ — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
Пример ДНФ: $f(x,y,z) = (x \land y) \lor (y \land \neg < z >)$
СДНФ — это такая ДНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых конъюнкций
- каждая простая конъюнкция полная
Пример СДНФ: $f(x,y,z) = (x \land \neg < y >\land z) \lor (x \land y \land \neg < z >)$
Теорема: Для любой булевой функции $f(\vec < x >)$, не равной тождественному нулю (), существует СДНФ, ее задающая.
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
$f(\vec < x >) = \neg x_i \wedge f(x_1, \dots ,x_ < i-1 >,0,x_ < i+1 >, \dots ,x_n) \vee x_i \wedge f(x_1, \dots ,x_ < i-1 >,1,x_ < i+1 >, \dots ,x_n)$
Данное соотношение легко проверить подстановкой всевозможных значений $x_i$ < $0$ и $1$ >. Эта формула позволяет выносить $x_i$ за знак функции. Последовательно вынося $x_1$, $x_2$. $x_n$ за знак $f(\vec < x >)$, получаем следующую формулу :
$ f(\vec < x >) = \neg x_1 \wedge \neg x_2 \wedge . \wedge \neg x_ < n-1 >\wedge \neg x_n \wedge f(0,0. 0,0)
$\neg x_1 \wedge \neg x_2 \wedge . \wedge \neg x_ < n-1 >\wedge x_n \wedge f(0,0. 0,1)
x_1 \wedge x_2 \wedge . \wedge x_ < n-1 >\wedge \neg x_n \wedge f(1,1. 1,0)
$ $x_1 \wedge x_2 \wedge . \wedge x_ < n-1 >\wedge x_n \wedge f(1,1. 1) $
Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от $n$ переменных мы имеем < < < $2^ < n >$ > > > конъюнктов. Каждый из них соответствует значению функции на одном из < < < $2^ < n >$ > > > возможных наборов значений $n$ переменных. Если на некотором наборе $f(\vec < x >)=0$, то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же $ f(\vec < x >)=1$, то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.
Алгоритм построения СДНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
- Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Пример построения СДНФ для медианы
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
| x | y | z | $\langle x,y,z \rangle$ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
| x | y | z | $ \langle x,y,z \rangle $ | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | $(\neg < x >\land y \land z)$ |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | $(x \land \neg < y >\land z)$ |
| 1 | 1 | 0 | 1 | $(x \land y \land \neg < z >)$ |
| 1 | 1 | 1 | 1 | $(x \land y \land z)$ |
Все полученные конъюнкции связываем операциями дизъюнкции. $ \langle x,y,z \rangle = (x \land y \land z) \lor (\neg < x >\land y \land z) \lor (x \land \neg < y >\land z) \lor (x \land y \land \neg < z >)$
Примеры СДНФ для некоторых функций
Стрелка Пирса: $x \downarrow y = (\neg < x >\land \neg < y >)$
Исключающее или: $x \oplus y \oplus z = (\overline < x >\land \overline < y >\land z) \lor (\overline < x >\land y \land \overline < z >) \lor (x \land \overline < y >\land \overline < z >) \lor (x \land y \land z)$
Совершенной дизъюнктивной нормальной формой формулы $A(x_1,x_2,…,x_n)$ называется ДНФ, обладающая следующими свойствами:
а > в ней нет одинаковых дизъюнктивных элементов;
б > ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в > ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
г > в каждой элементарной конъюнкции содержится либо $X_i$, либо $\overline < X >_i$, где $i = 1, n$.
Условие а > – г > являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
1) если какая-нибудь элементарная конъюнкция не содержит высказывание $X_i$, то заменим выражением $B\wedge (X_i\vee \overline < X >_i) \equiv (B\wedge X_i)\vee (B\wedge \overline < X >_i)$;
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Формула называется дизъюнктивной нормальной формой < ДНФ >, если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде: $A_1\vee A_2\vee . \vee A_n$ , где каждое $A_n$ — элементарная конъюнкция.
Формула $A$ от $k$ переменных называется совершенной дизъюнктивной нормальной формой < СДНФ >, если:
$A$ является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция $k$ переменных $x_1,x_2,…,x_k$, причем на $i$-м месте этой конъюнкции стоит либо переменная $x_i$ либо ее отрицание;
Все элементарные конъюнкции в такой ДНФ попарно различны.
Например: $A = x_1 \wedge$ НЕ $x_2 \vee x_1 \wedge x_2$
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций < дизъюнктивных членов >в ней.
Она является примером однозначного представления булевой функции в виде формульной < алгебраической >записи.
Теорема о СДНФ: Пусть $f(x_1 x_2, …, x_n)$ – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию $f$.
Алгоритм построения СДНФ по таблице истинности:
- В таблице истинности отмечаем наборы переменных, на которых значение функции $f = 1$.
- Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае – ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Далее:
Соленоидальное векторное поле
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана
Механические и физические приложения поверхностного интеграла первого рода
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Класс $L$. Теорема о замкнyтости класса $L$
Решение задач с помощью алгебры высказываний
Полином Жегалкина. Пример.
Класс Te . Теорема о замкнутости Te
Введение
Логические следствия
Теорема о полныx системаx в Pk
Поверхностный интеграл первого рода и его свойства
Свойства двойного интеграла
Огравление $\Rightarrow $
Источник
Таблица истинности
Инструкция . При вводе с клавиатуры используйте следующие обозначения:
| Клавиша | Оператор | |
|---|---|---|
| ! | ¬ | Отрицание (НЕ) |
| | | | | Штрих Шеффера (И-НЕ) |
| # | ↓ | Стрелка Пирса (ИЛИ-НЕ) |
| * | & | Конъюнкция (И) |
| + | v | Дизъюнкция (ИЛИ) |
| ^ | ⊕ | Исключающее ИЛИ, сумма по модулю 2 (XOR) |
| @ | → | Импликация (ЕСЛИ-ТО) |
| % | ← | Обратная импликация |
| = | ≡ ( |
, ↔)
bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис.
Правила ввода логической функции
- Вместо символа v (дизъюнкция, ИЛИ) используйте знак + .
- Перед логической функцией не надо указывать обозначение функции. Например, вместо F(x,y)=(x|y)=(x^y) необходимо ввести просто (x|y)=(x^y) .
- Максимальное количество переменных равно 10 .
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.
Источник
Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
СДНФ обладает некоторыми определенными свойствами:
- включает различные элементарные конъюнкции;
- все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
- ни в одном логическом слагаемом не содержится переменная и её отрицание.
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
- в ней отсутствуют одинаковые элементарные дизъюнкции;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
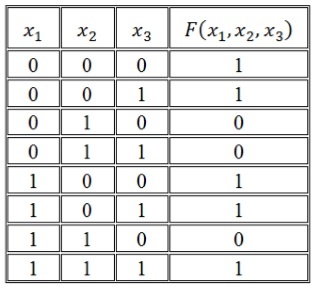
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
- Отметить наборы переменных, значение функции F на которых равно 1.
- Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
- Связать полученные конъюнкции операциями дизъюнкции.
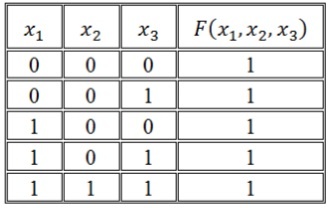
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
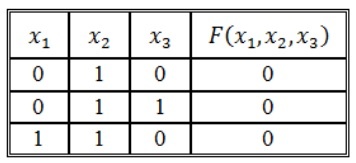
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
- Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
- Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
- Связать полученные дизъюнкции операциями конъюнкции.
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: \( \equiv , = , \Leftrightarrow .\)
Доказать эквивалентность формул можно двумя способами.
- Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
- Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
Склеивание
Обобщенное склеивание
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)
Расщепление
\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)
Примеры с решением
Задача №1
Приведите к СКНФ \(((((A\rightarrow B)\rightarrow\overline A)\rightarrow\overline B)\rightarrow\overline C)\) .
Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:
\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)
\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)
\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)
\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)
Далее приведем выражение к КНФ:
\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)
Далее приведем выражение к СКНФ:
\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)
\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)
\(f(\widetilde x^3) = (\overline
\(f(\widetilde x^3) = (\overline
\(=(\overline
Источник