Составить множества по 4 способам

Составить множества по 4 способам

Введение в теорию множеств и комбинаторику

Практическая работа № 1. Способы задания множеств

Вопросы к работе

1. Какие множества называются конечными, какие бесконечными, какие пустыми? Приведите примеры конечных, бесконечных, пустых множеств.

2. Что значит задать множество?

3. Что значит задать множество пересечением элементов? Когда это можно сделать? Приведите пример множеств, заданных пересечением элементов.

4. Что значит задать множество указанием характеристического свойства элементов? Приведите примеры множеств, заданных указанием характеристического свойства элементов.

5. Дайте определение характеристического свойства элементов множества.

Образцы решения заданий

Пример 1. Задать с помощью характеристического свойства элементов множество всех положительных чисел.

Ответ: .

Пример 2. Задать перечислением элементов множества, заданные указанием характеристического свойства элементов:

. Ответ: М = <1; 2; 3; 4>.

Пример 3. Указать стандартное обозначение множества М и изобразить его на числовой прямой:

1. Приведите примеры множеств, составленных из объектов следующих видов:

а) неодушевленных предметов;

г) геометрических фигур;

д) населенных пунктов;

ж) политических деятелей.

2. Назовите элементы, принадлежащие множеству:

а) студентов вашей группы;

б) предметов, изучаемых в I семестре вашей специальности;

в) всех частей света;

г) субъектов федерации, входящих в Российскую Федерацию.

3. Пусть А – множество многоугольников. Принадлежат ли этому множеству:

4. Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?

5. Прочитайте запись и укажите, какие из указанных высказываний истина, а какие ложь:

а) 270 N ; ж) -3 Z ;

б) 0 N ; з) Q ;

в) –3 N ; и) R ;

г) 1 Q ; к) sin 2,3 R ;

д) –7 N ; л) tg R .

е) 22 N ;

6. Пусть Е – множество европейских государств, А – множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?

а) Франция Е ; з) Волга Е ;

б) Испания Е ; и) Нигерия А ;

в) Монголия А ; к) Гималаи А ;

г) Индия А ; л) Япония А ;

д) Ирак Е ; м) Альпы Е ;

е) Турция А ; н) Швеция А .

ж) Байкал А ;

7. Запишите перечислением элементов следующие множества:

а) А – множество нечетных чисел на отрезке [1; 15];

б) В – множество натуральных чисел, меньших 8;

в) С – множество натуральных чисел, больших 10, но меньших 12;

г) D – множество двузначных чисел, делящихся на 10;

д) Е – множество натуральных делителей числа 18;

е) F – множество чисел, модуль которых равен .

8. Запишите перечислением элементов следующие множества:

а) множество различных букв в слове «головоломка»;

б) множества цифр числа 134433154.

9. Изобразите на числовой прямой множество решений неравенства с одним неизвестным x :

10. Выясните, множество решений какого неравенства изображено на числовой прямой в каждом случае:

1. Прочитайте следующие записи и перечислите элементы каждого из множеств:

Источник

Способы задания множеств

Задачи по математике для 3 класса

Задание 1

Найди общее свойство всех предметов, изображённых на рисунке:

Решение
• а) Прямоугольные предметы.
• б) Розовые предметы.
• в) Предметы цилиндрической формы.
• г) Стеклянные предметы.
• д) Инструменты.
• е) Одежда.

Задание 2

• а) Назови 5 элементов множества ягод.
• б) Назови 3 элемента множества грибов. Какие съедобные грибы ты знаешь? Какие грибы несъедобные?
• в) Назови 2 элемента множества книг. Есть ли у тебя любимые книги?
• г) Назови 4 элемента множества растений. Объясни, почему надо беречь растения.
• д) Задай какое-нибудь множество с помощью свойства и назови один предмет, принадлежащий этому множеству, и один предмет, который ему не принадлежит.

Решение
• а) Вишня, черешня, смородина, клюква, малина.
• б) Мухомор, поганка, подосиновик. Мухомор, поганка — ядовитые грибы. Белый гриб, боровик — съедобные грибы.
• в) Азбука, букварь — мои любимые книги.
• г) Трава, деревья, цветы, кустарники. Растения дают кислород, поэтому их надо беречь.
• д) Лекарства — лечат от болезней, продаются в аптеке. Аспирин принадлежит к множеству лекарств, хлеб не принадлежит.

Задание 3

Что сдавала в багаж дама из стихотворения С. Я. Маршака? Перечисли все элементы этого множества. Принадлежит ли этому множеству стол?

Задание 4

Перечисли множество предметов, которые лежат у тебя в портфеле. Принадлежат ли ему арбуз, самолёт, ручка?

Арбуз, самолёт не принадлежит к этому множеству. Ручка принадлежит.

Задание 5

• а) Перечисли множество девочек класса, сидящих в первом ряду.
• б) Перечисли множество вторых классов в твоей школе.
• в) Придумай множество, в котором легко перечислить элементы.

Решение
• а) Таня, Лена, Света.
• б) А, Б, В.
• в) Множество моей семьи. Папа, мама, я, брат, бабушка, дедушка.

Задание 6

Задай множество общим свойством его элементов:

Задание 7

• а) А — множество букв в слове «крот».
• б) В — множество нечётных однозначных чисел.
• в) С — множество двузначных чисел, кратных 10.
• г) D — множество трёхзначных чисел, больших 603, но меньших 608.

Задай множество перечислением:

Задание 8

• 7 + 8 =
• 16 + 4 =
• 8 + 15 =
• 21 + 34 =
• 12 — 5 =
• 39 — 9 =
• 42 — 8 =
• 36 — 14 =
• 27 + 43 =
• 36 + 17 =
• 50 — 32 =
• 85 — 39 =

Решение
• 7 + 8 = 15
• 16 + 4 = 20
• 8 + 15 = 23
• 21 + 34 = 55
• 12 — 5 = 7
• 39 — 9 = 30
• 42 — 8 = 34
• 36 — 14 = 22
• 27 + 43 = 70
• 36 + 17 = 53
• 50 — 32 = 18
• 85 — 39 = 46

Задача 9

Задача 10

В один день Ира прочитала 21 страницу, во второй — в 2 раза больше, чем в первый, а в третий — на 15 страниц меньше, чем во второй день. Сколько страниц прочитала Ира за 3 дня?

Решение
• Вычисляем сколько страниц прочитала Ира во второй день: 2 * 21 = 42.
• Вычисляем сколько страниц прочитала Ира в третий день: 42 — 15 = 27.
• Вычисляем сколько страниц прочитала Ира за 3 дня : 21 + 42 + 27 = 90.
• ОТВЕТ: Ира прочитала за 3 дня 90 страниц.

Задача 11

Вырази в сантиметрах и вычисли:

• а) 3 м 7 дм 6 см + 4 м 3 дм 8 см
• б) 1 м 6 дм 9 см + 47 дм 2 см
• в) 9 м 72 см — 5 дм 9 см
• г) 7 м 4 см — 32 дм 6 см

Решение
• а)
  • 3 м 7 дм 6 см = 376 см
  • 4 м 3 дм 8 см = 438 см
  • 376 см + 438 см = 814 см
• б)
  • 1 м 6 дм 9 см = 169 см
  • 47 дм 2 см = 472 см
  • 169 см + 472 см = 641 см
• в)
  • 9 м 72 см = 972 см
  • 5 дм 9 см = 59 см
  • 972 см — 59 см = 913 см
• г)
  • 7 м 4 см = 704 см
  • 32 дм 6 см = 326 см
  • 704 см — 326 см = 378 см

Задача 12

Соедини последовательно точки, соответствующие ответам примеров. Что получилось?

Источник

Способы задания множеств.

ПЛАН

1. Понятие множества.

2. Способы задания множеств.

3. Отношения между множествами.

4. Операции над множествами.

5. Свойства операций над множествами.

6. Понятие «система счисления».

7. Непозиционная система счисления.

8. Позиционная система счисления.

9. Перевод чисел из одной системы счисления в другую.

Понятие множества.

Для сокращенной записи будем использовать следующие символы:

• a Î A — а является элементом множества А;

• a Ï A — а не является элементом множества А;

• — пустое множество;

• <a, d, с> — множество, состоящее из трех элементов a, d и с;

• <х|Р(х)> — множество, состоящее из таких элементов х, для которых истинно утверждение Р(х);

• A È B — объединение множеств A и В;

• A Ç B — пересечение множеств А и В;

• A Ì B — А является подмножеством В;

• — дополнение множества А до универсального множества;

• U — универсальное множество;

• a R b — между a и b существует бинарное отношение R.

Множество является самым широким понятием в математике и поэтому принимается без определения. Множество считается заданным, если относительно каждого объекта можно сказать, принадлежит он данному множеству или нет. Поэтому обычно говорят о множестве как о наборе предметов (элементов множества), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли — всё это примеры множеств.

Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.

Пустое множество ( ) не содержит ни одного элемента, например, множество крылатых слонов, множество корней уравнения sin x = 2 и т.д.

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.

Счётное множество — множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке) или бесконечным (множество целых чисел, его элементы можно пронумеровать следующим образом:

элементы множества: . -5, — 4, -3, -2, -1, 0, 1, 2, 3, 4, 5, .

номера элементов: . 11 9 7 5 3 1 2 4 6 8 10 . ).

Несчётное множество — множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным.

Выпуклое множество — множество, которое наряду с любыми двумя точками А и В содержит также весь отрезок АВ. Примеры выпуклых множеств: прямая, плоскость, круг. Однако, окружность не является выпуклым множеством.

Способы задания множеств.

Если объект a является элементом множества A, то говорят, что a принадлежит A, и записывают a A . Запись a Ï A означает, что a не принадлежит A.

Множество может быть задано следующим образом:

• перечислением всех его элементов по их названиям (так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);

Множество можно задать перечислением всех его элементов в любом порядке. Если множество A, например, состоит из первых четырех букв русского алфавита, то записывают

• заданием общей характеристики (общих свойств) элементов данного множества (например, множество рациональных чисел, собаки, семейство кошачьих и т.д.);

Множество может быть задано с помощью характеристического свойства, т.е. такого свойства, которым обладают все элементы данного множества и не обладают никакие другие объекты. Если множество A задано с помощью характеристического свойства P, то записывают A = <x|p(x)>

Например, запись A = <x|x R,—7

N — множество натуральных чисел;

Z — множество целых чисел;

Q — множество рациональных чисел;

R — множество действительных чисел.

Пример 1.1. Запишем различными способами множество A, элементами которого являются натуральные числа, не превосходящие числа 6.

Решение. Натуральными числами, не превосходящими числа 6, являются: 1, 2, 3, 4, 5, 6. Поэтому множество A можно записать так: A = <1, 2, 3, 4, 5, 6>, или A = <1, 3, 5, 2, 4, 6>, или A = <6, 5, 4, 3, 2, 1>, или перечислением элементов в каком-либо другом порядке.

По условию множество A задано описанием характеристического свойства его элементов «Быть натуральным числом, не превосходящим числа 6». Используя это свойство, множество можно записать так: A = <x|x N,x б>.

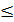
Пример 1.2. Прочитаем различными способами следующие записи:

а) 37 N ;

Решение. а) Число 37 является натуральным. Число 37 принадлежит множеству N. Число 37 — элемент множества N. Число 37 содержится во множестве N. Множество N содержит число 37.

б) Число 2,5 не является натуральным. Число 2,5 не принадлежит множеству N. Число 2,5 не является элементом множества N. Число 2,5 не содержится во множестве N. Множество N не содержит числа 2,5.

Пример 1.3. Используя понятие характеристического свойства, зададим следующие множества:

Решение. Множества A, B и C заданы способом перечисления элементов. Используя характеристические свойства, указанные множества можно задать следующим образом:

A — множество согласных букв русского алфавита;

B — множество цветов радуги;

C — множество дней недели.

Пример 1.4. Изобразим на числовой прямой элементы следующих множеств:

б) A = <x|x Z,—4 x

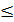
Источник