- Граф и график соответствия. Соответствие, обратное данному. Виды соответствий
- Тема 3. Понятие соответствия Содержание
- 1. Понятие соответствия между множествами
- Рассмотрим примеры соответствий, изучаемых в начальном курсе математики.
- 2. Способы задания соответствий
- 3. Соответствие обратное данному
- Презентация по ТОНКМ с методикой обучения на тему «Отношения и соответствия»
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Граф и график соответствия. Соответствие, обратное данному. Виды соответствий
Понятие соответствия. Способы задания соответствий
СООТВЕТСТВИЯ МЕЖДУ ДВУМЯ МНОЖЕСТВАМИ
Лекция 16. Соответствия
1. Понятие соответствия. Способы задания соответствий.
2. Граф и график соответствия. Соответствие, обратное данному. Виды соответствий.
3. Взаимно-однозначные соответствия
Первоначально алгеброй называли учение о решении уравнений. За много столетий своего развития алгебра превратилась в науку, которая изучает операции и отношения на различных множествах. Поэтому не случайно уже в начальной школе дети знакомятся с такими алгебраическими понятиями, как выражение (числовое и с переменными), числовое равенство, числовое неравенство, уравнение. Они изучают различные свойства арифметических действий над числами, которые позволяют рационально выполнять вычисления. И конечно, в начальном курсе математики происходит их знакомство с различными зависимостями, отношениями, но чтобы использовать их в целях развития мыслительной деятельности детей, учитель должен овладеть некоторыми общими понятиями современной алгебры — понятием соответствия, отношения, алгебраической операции и др. Кроме того, усваивая математический язык, используемый в алгебре, учитель сможет глубже понять сущность математического моделирования реальных явлений и процессов.
Изучая окружающий нас мир, математика рассматривает не только его объекты, но и главным образом связи между ними. Эти связи называют зависимостями, соответствиями, отношениями, функциями. Например, при вычислении длин предметов устанавливаются соответствия между предметами и числами, которые являются значениями их длин; при решении задач на движение устанавливается зависимость между пройденным расстоянием и временем, если скорость движения постоянна.
Конкретные зависимости, соответствия, отношения между объектами в математике изучались с момента ее возникновения. Но вопрос о том, что общее имеют самые разные соответствия, какова сущность любого соответствия, был поставлен в конце XIX — начале XX века, и ответ на него был найден в рамках теории множеств.
В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств. Поэтому учителю надо понимать их суть, что поможет ему обеспечить единство в методике изучения этих взаимосвязей.
Рассмотрим три примера соответствий, изучаемых в начальном курсе математики.
| I. Найти значение выражения: | II.Найти площадь фигуры | III. Решить уравнение: |
| в1) (17-1):4; в2) (12 + 18) : (6-6); в3) 2·7 + 6. | y1) 2 + x = 6; y2) x – 7 = 4; y3) 2x = 8 |
В первом случае мы устанавливаем соответствие между заданными выражениями и их числовыми значениями. Во втором выясняем, какое число соответствует каждой из данных фигур, характеризуя ее площадь. В третьем ищем число, которое является решением уравнения.
Что общее имеют эти соответствия?
Видим, что во всех случаях мы имеем два множества: в первом -это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором -это множество из трех геометрических фигур и множество N натуральных чисел; в третьем — это множество из трех уравнений и множество N натуральных чисел.
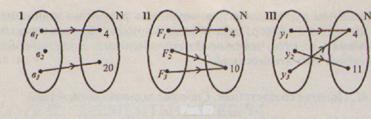
Выполняя предложенные задания, мы устанавливаем связь (соответствие) между этими множествами. Ее можно представить наглядно, при помощи графов (рис. 67).
Можно задать эти соответствия, перечислив все пары элементов, плодящихся в заданном соответствии:
Рис. 67
Полученные множества показывают, что любое соответствие между двумя множествами X и Y можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары — это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.
Определение.Соответствием между множествами X и Y называется всякое подмножество декартова произведения этих множеств.
Соответствия принято обозначать буквами Р, S, Т, К и др. Если S -соответствие между элементами множеств X и Y то, согласно определению, S с Х х У.
Выясним теперь, как задают соответствия между двумя множествами. Поскольку соответствие — это подмножество, то его можно задавать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества. Так, соответствие между множествами X — <1, 2, 4, 6>и У = <3, 5>можно задать:
1) при помощи предложения с двумя переменными: а -1 , то S -1 = <(2,4), (3,5), (6,8)>.
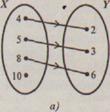 |
Рис.70
Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: хSу. Запись хSу можно рассматривать как обобщение записей конкретных соответствий: x= 2у; х > 3у+1 и др.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Тема 3. Понятие соответствия Содержание
Понятие соответствия между множествами.
Способы задания соответствий.
Соответствие обратное данному.
Взаимно однозначное соответствие.
Равномощные множества. Счетные множества.
Основная литература 7, 10, 11, 16, 23, 33, 34;
Дополнительная литература 1, 10, 14, 74
1. Понятие соответствия между множествами
В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств. Поэтому учителю надо понимать их суть, что поможет ему обеспечить единство в методике этих взаимосвязей.
Рассмотрим примеры соответствий, изучаемых в начальном курсе математики.
Пример 1. а) (17 – 1) : 4; б) (12 + 18) : (6-6); в) 27 + 6. Пример 2. 1) 2+х =6; 2) х-7=4; 3) 2х=8.
В первом примере мы установили соответствие между заданными выражениями и их числовыми значениями. Во втором выяснили, какое число является решением уравнения.
Все эти соответствия имеют общее – во обоих случаях мы имеем два множества: в первом – это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором – это множество из трех уравнений и множество N натуральных чисел.
Связь (соответствие) между этими множества можно представить наглядно, при помощи графов.

Полученные множества показывают, что любое соответствие между двумя множествами Х и У можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары – это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.
Определение. Соответствием между множествами Х и У называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами R, P, F, T и др.
2. Способы задания соответствий
Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества.
Пример. Соответствие между множествами Х = 1, 2, 4, 6 и У = 3, 5 можно задать: 1) при помощи предложения с двумя переменными: а в при условии, что а Х, в У; 2) перечислив пары чисел, принадлежащих подмножеству декартова произведения ХУ: (1,3),(1,5),(2,3),(2,5),(4,5). К этому способу задания относят также задание соответствия при помощи графа и графика.
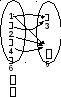
3. Соответствие обратное данному
Пример. Пусть S – соответствие «больше на 2» между множествами Х = 4, 5, 8, 10 и У = 2, 3, 6. Тогда S = (4,2), (5,3), (8,6) и его граф будет как на рисунке.
С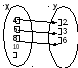
Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: х S у.
Определение. Пусть S – соответствие между множествами Х и У. Соответствие S -1 между множествами У и Х называется обратным данному, если у S -1 х тогда и только тогда, когда х S у. Соответствия S и S -1 называют взаимно обратными.
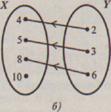
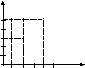
Выясним особенности их графиков. Построим график соответствия S = (4,2), (5,3), (8,6)
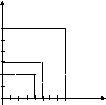
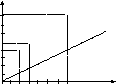
При построении графика соответствия S -1 = (2,4), (3,5), (6,8) мы должны первую компоненту выбирать из множества У = 2,3,6, а вторую – из множества Х = 4, 5, 8, 10. В результате график соответствия S -1 совпадет с графиком соответствия S. Чтобы различать графики соответствий S и S -1 , условились первую компоненту пары соответствия S -1 считать абсциссой, а вторую – ординатой. Например, если (5,3) S, то (3,5) S -1 . Точки с координатами (5,3) и (3,5), а в общем случае (х,у) и (у,х) симметричны относительно биссектрисы 1-го и 3-го координатных углов. Следовательно, графики взаимно обратных соответствий S и S -1 симметричны относительно биссектрисы 1-го и 3-го координатных углов.
Чтобы построить график соответствия S -1 , достаточно изобразить на координатной плоскости точки, симметричные точкам графика S относительно биссектрисы 1-го и 3-го координатных углов.
Источник
Презентация по ТОНКМ с методикой обучения на тему «Отношения и соответствия»
Описание презентации по отдельным слайдам:
Отношения и соответствия План: Отношения между элементами одного множества. Понятие отношения, способы задания. Свойства отношений. Отношение эквивалентности и порядка. Соответствие между элементами двух множеств. Понятие соответствия, способы задания. Взаимно однозначные соответствия. Задания для самостоятельной работы. Вопросы для самоконтроля.
В математике рассматривают связи между элементами одного множества и называют их отношениями. Если рассматривают отношения между двумя элементами, то их называют бинарными. Отношения многообразны: между понятиями – это отношения род и вида, части и целого; между предложениями – это отношения следования и равносильности; между числами – «больше», «меньше», «равно», «больше на…» и т. п.
Рассмотрим на множестве отрезков на рис.1 отношения перпендикулярности равенства «длиннее» Рисунок1 Построим графы данных отношений. Сравним их и выделим свойства.
Рисунок 2 «Граф отношений равенства»
Рисунок 3 «Граф отношения перпендикулярности»
Рисунок 4 «Граф отношения длиннее»
Определение. Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой. На графе: «петля» в каждой вершине графа. Рефлексивны отношения: равенства (рисунок 2 «каждый отрезок равен сам себе»). кратности (каждое N число кратно самому себе). подобия.
На графе: две вершины соединены только одной стрелкой. Существуют отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности. Пример. Дано отношение «быть сестрой» на множестве детей одной семьи: Катя, Маша, Толя. К М Т
Если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества (классы эквивалентности). Верно и обратное утверждение. Определение. Отношение R на множестве Х называется отношением порядка, если оно транзитивно и антисимметрично. Является отношением порядка отношения: «меньше» «длиннее»
Данное соответствие взаимно однозначное, т.к. каждому соответствует единственный
Курс повышения квалификации
Охрана труда
- Сейчас обучается 95 человек из 44 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 335 человек из 66 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 171 человек из 47 регионов
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-092237
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Пензенской области запустят проект по снижению административной нагрузки на учителей
Время чтения: 1 минута
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Минобрнауки учредит именные стипендии для студентов из малочисленных народов
Время чтения: 1 минута
Спортивные и творческие кружки должны появиться в каждой школе до 2024 года
Время чтения: 1 минута
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Российский совет олимпиад школьников намерен усилить требования к олимпиадам
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник