- Соответствия между множествами
- 16. Понятие соответствия между элементами двух множеств. Способы задания соответствий. Соответствие обратное данному.
- Понятие соответствия между элементами двух множеств. Способы задания соответствий. Соответствие обратное данному. Взаимно однозначные соответствия. Равномощные множества
- §8. Понятие соответствия между множествами. Способы задания соответствий
- Соответствие между элементами множеств. Способы задания соответствий
Соответствия между множествами
Изучая окружающий нас мир, математика рассматривает не только его объекты, но связи между ними. Эти связи называют зависимостями, соответствиями, отношениями, функциями. Например, при вычислении длин предметов устанавливаются соответствия между предметами и числами, которые являются значениями их длин; при решении задач на движение устанавливается зависимость между пройденным расстоянием и временем при условии, что скорость движения постоянна. Начальная частная школа помогает учащимся устанавить соответствие между заданными выражениями и их числовыми значениями, между числом, характеризующим площадь данной фигуры, и самой этой фигурой и т.п.
Соответствием между множествами X и Y называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами P, S, T, R и др. Если xSy – соответствие между элементами множеств X и Y, то, соглаcно определению, S

Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества. Например, соответствие между множествами X= и Y= можно задать: 1) при помощи предложения с двумя переменными: a Просмотров 82 151 Комментариев 2
Источник
16. Понятие соответствия между элементами двух множеств. Способы задания соответствий. Соответствие обратное данному.
Соответствием между множествами Х и У наз. всякое подмножество декартова произведения множества Х на множество У.
Мы можем перечислить все пары элементов. Мы можем построить граф соответствия R.
Мы можем построить график
Для любого соответствия можно построить соответствие, обратное данному.
Пусть S соответствие между множествами х и у. Тогда соответствие S -1 между множествами у и х наз.обратным данному, если элемент у находится в соответствии с S -1 в соответствии с элементом х, тогда и только тогда, когда элемент х находится в соответствии S с элементом у.
Граф обратный данному R -1 : «у 0 y = 2x
1) Область определения множества (D(f)) – любое действ. число (R) (от- беск., до +беск.)
2) область значения (Е(х)) – все действительные числа (R) (от- беск., до +беск.)
3) При к 0 функция возрастает на всей области определения.
4) отношение двух значений аргумента равно отношению соответственных значений функции, т.е. х1 : х2 = у1 : у2.
Если х и у – положительные числа, то с увеличением значения переменной х в несколько раз соответствующие значения функция возрастает во столько же раз.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Понятие соответствия между элементами двух множеств. Способы задания соответствий. Соответствие обратное данному. Взаимно однозначные соответствия. Равномощные множества



Соответствие между элементами мн-в А и В называют любое под множ-во их декартово произведения.
Способы задания соответствия
1 – указаниям характеристик св-ва по кот. Эти пары составл.
2- перечисление этих пар.
Пример: если мн-ва
3)С помощью графа.
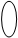 |  |
4)С помощью таблицы
| X/Y | |||
| (1,1) | (1,3) | (1,5) | (1,7) |
| (2,1) | (2,3) | (2,5) | (2,7) |
| (3,1) | (3,3) | (3,5) | (3,7) |
Определение:
Между элементами назыв обратно данному если yS (В минус 1 степени) xó xSy
S(В минус первой степени) входит B x А.
Чтобы постр графического обратного соответствия надо поменять направления стрелок.
Чтобы задать соответствие обратное данному в перечисление пар надо поменять местами компоненты пар. Графики взаимно обратных соответствий семетричны. Относительно прямой координатных углов.
Определение:
Взаимно однозначном соответствием между элементам мн-в А и В назыв. такое соответствие при которым каждому элементу. Из мн-в А соответствует единст элемент.
Из мн-ва В и каждый элемент из мн-ва В является соответсвующим только для одного элемента из мн-ва А.
Пример: Мн-во первых 24 натур чисел, мн-во студен в группе.
Мн-во А и В назыв равномощным если между их элементами можно установить взаимно однозначно А
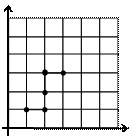
2. Обучающимся начальных классов предложено задание:
 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 |
• При изучении какой темы курса математики начальных классов можно предложить это задание?
• С какой целью и на каком этапе?
• Соответствие между какими множествами здесь задается? Являются ли эти множества равномощными?
• Опишите методику введения знаков ”>“ и “
Источник
§8. Понятие соответствия между множествами. Способы задания соответствий
Пусть заданы два множества X и Y. Если для каждого элемента х Î Х указан элемент y Î Y, с которым сопоставляется х, то говорят, что между множествами X и Y установлено соответствие.
Иначе говоря, соответствием между элементами множеств X и Y называется любое подмножество G декартова произведения X ´ Y этих множеств. Если (х, у) Î G, то множество первых компонентов (D(G)) называется областью определения соответствия G, множество вторых компонентов (E(G)) –– областью значений этого соответствия.
Множество всех y Î Y, которые сопоставляются элементу х Î Х, называется образом х в Y. Множество же всех х Î Х, которым сопоставляют элемент y Î Y, называется прообразом y в Х.
Способы задания соответствия. Поскольку соответствие — это множество, то его можно задать теми же способами, что и любое множество: перечислением всех пар (х, у), где элементы х Î Х и y Î Y связаны данным соответствием; указанием характеристического свойства всех пар (х, у) элементов х Î Х, y Î Y, находящихся в рассматриваемом соответствии.
Когда множества X и Y конечные, то соответствие между элементами можно задать таблицей, где в левом столбце записывают элементы множества Х, а в верхней строке — элементы множества Y. Пары элементов, находящихся в соответствии G, будут находиться на пересечении соответствующих столбцов и строк.
Соответствие между двумя конечными множествами можно показать и при помощи графа. Множества X и Y показывают оваломи, элементы множеств X и Y обозначают точками, а стрелками соединяют соответствующие элементы так, что если имеет место (х, у) Î G, то стрелку проводят из точки х в точку у.
Когда множества Х и Y числовые, то можно построить график соответствия G на координатной плоскости.
Пример, график соответствия «меньше» между элементами множеств Х = <1, 3, 4, 6>и Y = <2, 5, 7>. Выпишем пары элементов, находящихся в данном соответствии: (1, 2), (1, 5), (1, 7), (3, 5), (3, 7), (4, 5), (4, 7), (6, 7). Если изобразить элементы множества Х на оси Ох, а элементы множества Y на оси Оу, а выписанные пары отметить точками на координатной плоскости, то получим график рассматриваемого соответствия между элементами множеств X и Y (рис. 13).
Источник
Соответствие между элементами множеств. Способы задания соответствий
Дата добавления: 2014-09-06 ; просмотров: 12001 ; Нарушение авторских прав
Учащимся некоторого класса был задан вопрос, какие кружки они посещают. Их ответы были занесены в таблицу:
| Музыкальный | Рисования | Танцевальный | Выжигания |
| Артем | |||
| Борис | |||
| Виктор |
Из таблицы видно, что Артем посещает 3 кружка, а Виктор только один; больше всего из опрошенных посещают кружок рисования и никто из них не посещает кружок выжигания…
В данном примере рассматриваются два множества: Х = <А; Б; В>– множество имен и Y = <м; р; т; в>– множество названий кружков.
При помощи слов «посещать какой-либо кружок» между элементами этих множеств установлена некоторая связь, или, как говорят в математике, соответствие. В таблице это соответствие выделено заштрихованными клетками, а множество всех клеток таблицы является декартовым произведением множеств Х и Y.
Соответствие между множествами Х и Y мы установили, имея 3 множества: множество Х – множество имен, множество Y – множество названий кружков и подмножество декартова произведения Х ´ Y.
Определение. Соответствием между множествами Х и Y называется любое подмножество R декартова произведения множеств Х и Y.
Множество Х называют множеством отправления соответствия, множество Y – множеством прибытия соответствия.
Если пара (х; у) Î R, то говорят, что элемент у соответствует элементу х; у является образом элемента х; х является прообразом элемента у.
Определение. Множество всех первых компонент пар, входящих в соответствие, называется областью определения соответствия.
Определение. Множество всех вторых компонент пар, входящих в соответствие, называется областью значений соответствия.
Т.к. соответствие – подмножество декартова произведения, то способы задания соответствий такие же, как и для декартова произведения.
R – «х – делитель у» – соответствие задано указанием характеристического свойства;
R = <(2; 6); (3; 6); (3; 9); (3; 15); (5; 15)>– соответствие задано перечислением. Также соответствие можно задать таблицей:
|
графом: графиком:
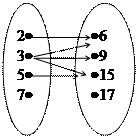 |
В нашем примере элементу 3 соответствует три элемента множества Y – 6, 9 и 15. Множество, состоящее из чисел 6, 9 и 15, называют образом элемента 3.
В общем случае, образ элемента х из множества Х определяется как множество всех элементов у Î Y, соответствующих элементу х.
Число 6 соответствует двум элементам множества Х – числам 2 и 3. Множество, состоящее из чисел 2 и 3, называют полным прообразом элемента 6 из множества Х.
В общем виде: полный прообраз элемента уÎY определяют как множество элементов х ÎХ, таких что элементу х соответствует элемент у.
Определение. Множество всех элементов из множества Х, имеющих непустые образы, называется областью (множеством) определения соответствия R.
Определение. Множество всех элементов из множества Y, имеющих непустой полный прообраз, называется множеством значений соответствия R.
В нашем примере: <2; 3; 5>– множество определения; <6; 9; 15>– множество значений.
Понятие соответствия между множествами относится к числу фундаментальных понятий математики. Оно лежит в основе определения таких важнейших понятий математики, как функция и отображение. Кроме того, в любой науке изучаются не только сами объекты, но и связи между ними.
Источник