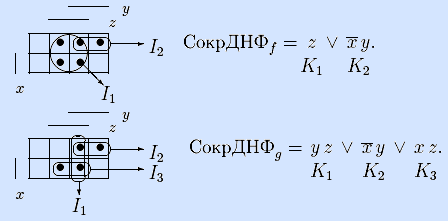- Сокращенная днф геометрический способ
- 35.Построение Сокращенных днф геометрическим методом. Пример.
- 36. Построение минимальных днф с помощью карт Карно.
- Сокращённая и минимальная ДНФ
- Содержание
- Сокращенная ДНФ [ править ]
- Минимальная ДНФ [ править ]
- Минимизация ДНФ [ править ]
- Визуализация гиперкубами [ править ]
- Карты Карно [ править ]
- Метод Квайна [ править ]
- Описание алгоритма [ править ]
- Пример [ править ]
Сокращенная днф геометрический способ
Определение. Булева функция g(x1, …, xn) называется импликантой функции f(x1, …, xn), если
Так как x 
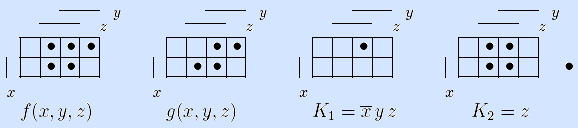
Примеры. Пусть функция f(x,y,z) задана матрицей Грея (левая матрица на рисунке). Функция g(x, y, z) и конъюнкции K1= x y z, K2= z (три правые матрицы) – ее импликанты.
Очевидно, что если K – любая конъюнкция ДНФf, то K является импликантой функции f(x1, …, xn) и задается допустимым для функции f(x1, …, xn) интервалом IK.
Определение. Элементарная конъюнкция K называется простой импликантой функции f(x1, …, xn),если она является импликантой этой функции, и не существует другой конъюнкции K’, которая является импликантой функции f(x1, …, xn) и поглощает конъюнкцию K.
Примеры. Рассмотрим функцию f(x,y,z) из предыдущего примера. Конъюнкция K2=z – простая импликанта данной функции, а конъюнция K1= x y z – импликанта, но не простая, так как она поглощается импликантой K2. •
Другими словами, простая импликанта функции – это такая импликанта-конъюкция, которая не может быть упрощена выбрасыванием из нее переменных, то есть неупрощаемая конъюнкция. Это означает, что всякая простая импликанта K булевой функции f(x1, …, xn) задается максимальным для этой функции интервалом IK.
Определение. ДНФ, состоящая из всех простых импликант булевой функции f(x1, …, xn), называется сокращенной ДНФ этой функции (или СокрДНФf).
Из определения следует, что сокращенная ДНФ единственна для данной функции, то есть наряду с СовДНФ и СовКНФ она является еще одной канонической формой представления булевой функции.
В общем случае построение сокращенной ДНФ является довольно сложной задачей, которая будет рассмотрена нами далее. Однако для булевой функции небольшого числа аргументов, заданной матрицей Грея, найти сокращенную ДНФ (или, что то же самое, множество всех максимальных интервалов ) довольно просто, и мы уже решали такую задачу для мажоритарной функции в подразделе 3.3, изучая интервальный способ задания булевой функции.
Примеры. Найдем сокращенные ДНФ функций из предыдущего примера: f(x,y,z), g(x,y,z), и функции h(x,y,z).
СокрДНФh сложнее – она состоит из шести простых импликант, поэтому для наглядности изображена на двух матрицах Грея:
Обратим внимание на то, что термин »сокращенная» относится не к длине ДНФ (она может быть большой, значительно больше длины совершенной ДНФ), а к рангам всех ее конъюнкций – ранги неупрощаемых конъюнкций (именно из них состоит сокращенная ДНФ) не могут быть уменьшены.
Источник
35.Построение Сокращенных днф геометрическим методом. Пример.
Установим геометрический смысл простой склейки с точки зрения «геометрии» булева куба. Простая склейка может быть применена только к таким двум элементарным конъюнкциям Ka и Kb, соответствующим наборам переменных a и b, что для некоторого i
Это значит, что наборы a и b таковы, что один из них доминирует над другим (они различаются значением только одной компоненты, значит a ≤ b или b ≤ a), т.е. они образуют ребро булева куба В n . Следовательно, простой склейке, применяемой к элементарным конъюнкциям исходной СДНФ, представляющей функцию, подлежат те и только те элементарные конъюнкции, которые соответствуют элементам какого-либо ребра булева куба, на котором функция принимает единичное значение. Образно говоря, две соседние вершины куба, на которых функция равна 1, «склеиваются» в ребро, их «соединяющее».
36. Построение минимальных днф с помощью карт Карно.
Метод минимизаций карт Карно:
Применяется для построения СДНФ функций четырех переменных.
В этом методе для функции f( 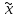
Клетка в таблице соответствующая вершинам куба в котором функция принимает значение 1 ставят Ӿ.
Гранью называют множество Ӿ карты соответствующей какой-либо грани четырехмерного куба.
Мощность грани – количество Ӿ.
Максимальной гранью для каждой Ӿ будем считать грань с наибольшей мощностью.
Полезной мощностью будем называть множество еще непокрытых Ӿ данной грани (0,1,2,…,m)(m-максимальная мощность грани)
Пример:f( 
Источник
Сокращённая и минимальная ДНФ
Содержание
Сокращенная ДНФ [ править ]
| Определение: |
Сокращенная ДНФ (англ. reduced disjunctive normal form) — форма записи функции, обладающая следующими свойствами:
|
Например: [math](x \land y)[/math] содержится в [math](x \land y \land z)[/math] .
Функцию можно записать с помощью сокращенной ДНФ не единственным способом.
Запишем функцию [math]\left\lt x, y, z\right\gt [/math] (медиана) в виде совершенной ДНФ: [math](x \land y \land z) \lor (x \land y \land \lnot z) \lor (x \land \lnot y \land z) \lor (\neg x \land y \land z)[/math] . Известно, что это выражение равносильно следующему: [math]((x \land y \land z) \lor (x \land y \land \lnot z)) \lor ((x \land \lnot y \land z) \lor (x \land y \land z)) \lor ((\neg x \land y \land z) \lor (x \land y \land z))[/math] . Вынесем в каждой скобке общий конъюнкт (например, в первой [math](x \land y \land z) \lor (x \land y \land \lnot z)=(x \land y) \lor (z \land \lnot z)[/math] . Так как [math]z \land \lnot z = 0[/math] , то такой конъюнкт не влияет на значение выражения, и его можно опустить. Получим в итоге формулу [math](x \land y) \lor (y \land z) \lor (x \land z)[/math] .
Минимальная ДНФ [ править ]
| Определение: |
| Минимальная ДНФ (англ. minimal disjunctive normal form) — такая сокращенная ДНФ, в которой содержится минимальное количество вхождений переменных. |
Каждая минимальная ДНФ является сокращенной, но не каждая сокращенная — минимальна. Например, запись [math](x \land y) \lor (y \land z) \lor (x \land z)[/math] является минимальной ДНФ для медианы (она же сокращенная, как видно в примере выше); а запись [math](x \land y \land \lnot z) \lor (\neg x \land y \land z) \lor (x \land z)[/math] — не минимальная, но сокращенная ДНФ.
Минимизация ДНФ [ править ]
Рассмотрим несколько способов минимизации дизъюнктивных нормальных форм:
Визуализация гиперкубами [ править ]
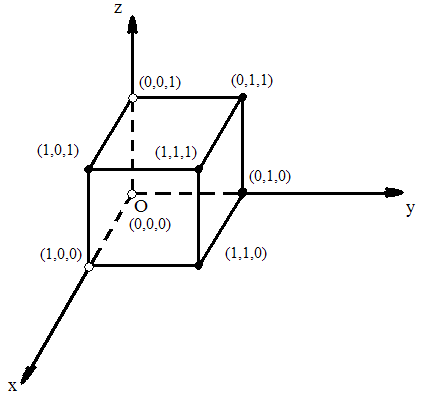
Этот способ работает при количестве переменных не больше трёх (в противном необходимо вводить четвёртое или следующие за ним измерения для представления фигур). Сначала мы рисуем куб в системе отсчёта [math]Oxyz[/math] (названия координатных осей соответствуют названиям переменных). Затем каждую вершину обрабатываем следующим образом:
| Описание алгоритма | Пример |
| Если у нас конъюнкт, переменные в котором равны соответствующим координатам вершины, то в эту вершину мы помещаем закрашенный чёрным кружок. | Вершине с координатами [math](0,1,1) [/math] соответствует конъюнкт [math](\neg X \wedge Y \wedge Z)[/math] , он равен единице при [math]X=0, Y=1[/math] и [math]Z=1[/math] ) |
| В противном случае мы помещаем в вершину закрашенный белый кружок. | Для такой ДНФ: [math](X \wedge \neg Y \wedge Z)\vee[/math] [math] (X \wedge Y \wedge Z) \vee [/math] [math] (\neg X \wedge Y \wedge Z) \vee[/math] [math] (\neg X \wedge Y \wedge \neg Z) \vee [/math] [math]( X \wedge Y \wedge \neg Z)[/math] мы получим следующий гиперкуб (см. рисунок) |
| Далее обработка гиперкуба идёт следующим образом: пока у нас есть незакрашенные вершины, мы выбираем грань, либо вершину, либо ребро, на которых больше всего закрашенных чёрным вершин и ещё не обработанных вершин. | |
| Если в данном гиперкубе есть грань, все вершины на которой закрашены чёрным, то мы можем записать её в качестве конъюнкта, где будет только переменная с неизменяющейся соответствующей ей координатой. | Грань, на которой лежат закрашенные вершины [math](0,1,1), (0,1,0), (1,1,0)[/math] и [math](1,1,1)[/math] мы можем записать как конъюнкт [math]Y[/math] . |
| Теперь мы смотрим, остались ли на рёбрах куба закрашенные и не отмеченные нами в ДНФ вершины. Если — да, то рёбра с такими вершинами мы можем записать в качестве конъюнкта, где будут только переменные с неизменяющимися соответствующим им координатами | Ребро, соединяющее закрашенные вершины [math](0,1,1)[/math] и [math](1,1,1)[/math] мы можем записать как конъюнкт [math](Y \wedge Z)[/math] . |
| И если после такой обработки у нас остались свободные вершины, мы просто переписываем координаты каждой такой вершины в отдельный конъюнкт, равный [math]1[/math] . | Вершину [math](1,0,1)[/math] мы бы переписали как конъюнкт [math](X \wedge \neg Y \wedge Z)[/math] . |
В итоге нашу изначальную ДНФ можно записать как [math](Y) \vee (X \wedge Z)[/math] .
Карты Карно [ править ]
Построим следующую таблицу [math]n \times n[/math] , где [math]n[/math] — число переменных:
| [math]w[/math] | [math]w[/math] | [math]\neg | [math]\neg |
|---|---|---|---|
| [math]z[/math] | [math]\neg | [math]\neg | [math]z[/math] |
| [math]y[/math] | [math]x[/math] | ||
| [math]y[/math] | [math]\neg | ||
| [math]\neg | [math]\neg | ||
| [math]\neg | [math]x[/math] |
Теперь для каждого конъюнкта мы помечаем соответствующую ему ячейку таблицы.
[math](\neg X \wedge Y \wedge \neg Z \wedge W) \vee (\neg X \wedge Y \wedge \neg Z \wedge \neg W) \vee (\neg X \wedge \neg Y \wedge \neg Z \wedge W) \vee (\neg X \wedge \neg Y \wedge \neg Z \wedge \neg W) \vee (\neg X \wedge \neg Y \wedge Z \wedge \neg W) \vee (X \wedge \neg Y \wedge \neg Z \wedge \neg W) \vee (X \wedge \neg Y \wedge Z \wedge \neg W)[/math]
будет выглядеть на картах Карно так:
| [math]w[/math] | [math]w[/math] | [math]\neg | [math]\neg |
|---|---|---|---|
| [math]z[/math] | [math]\neg | [math]\neg | [math]z[/math] |
| [math]y[/math] | [math]x[/math] | ||
| [math]y[/math] | [math]\neg | [math]1[/math] | [math]1[/math] |
| [math]\neg | [math]\neg | [math]1[/math] | [math]1[/math] |
| [math]\neg | [math]x[/math] | [math]1[/math] | [math]1[/math] |
Теперь покрываем прямоугольниками (длины сторон которых — степени двойки ( [math]1, 2, 4[/math] )) те ячейки карт Карно, которые содержат в себе единицу (на каждом ходу мы выбираем такой прямоугольник, чтобы он покрывал наибольшее количество ещё не покрытых клеток) до тех пор, пока не покроем все такие ячейки.
Для карт Карно на примере это выглядело бы так:
| [math]w[/math] | [math]w[/math] | [math]\neg | [math]\neg | |
|---|---|---|---|---|
| [math]z[/math] | [math]\neg | [math]\neg | [math]z[/math] | |
| [math]y[/math] | [math]x[/math] | |||
| [math]y[/math] | [math]\neg | [math]1[/math] | [math]1[/math] | |
| [math]\neg | [math]\neg | [math]1[/math] | [math]1[/math] | [math]1[/math] |
| [math]\neg | [math]x[/math] | [math]1[/math] | [math]1[/math] |
После этого записываем каждый прямоугольник в виде конъюнкта, в котором будут указаны только те переменные, которые одинаковы для всех ячеек этого прямоугольника.
То есть, в этом примере получаем: [math](\neg Z \wedge \neg X) \vee (\neg W \wedge \neg Y)[/math]
Метод Квайна [ править ]
Этот метод основан на применении двух основных операций:
- Операция попарного неполного склеивания:
[math]A x \lor A \neg x = A x \lor A \neg x \lor A[/math]
- Операция элементарного поглощения:
[math]A \tilde x \lor A = A [/math] (где [math]A[/math] — некоторая элементарная конъюнкция, то есть конъюнкт, в который каждая из переменных входит не более одного раза)
Пусть [math]A = y\neg z\neg w[/math] , тогда:
- Операция попарного неполного склеивания:
[math]y\neg z\neg w x \lor y\neg z\neg w \neg x = y\neg z\neg w x \lor y\neg z\neg w \neg x \lor y\neg z\neg w[/math]
- Операция элементарного поглощения:
[math]y\neg z\neg w \tilde x \lor y\neg z\neg w = y\neg z\neg w[/math]
Метод состоит в последовательном выполнении всех возможных склеиваний и затем всех поглощений частей СДНФ пока это может быть осуществимо.
Описание алгоритма [ править ]
- Исходным является множество пар вида [math]Ax[/math] или [math]A \neg x[/math]
- Выполняются все возможные операции неполного попарного склеивания для элементарных конъюнкций длины [math] n[/math] (где [math] n[/math] — число аргументов).
- Выполняются все возможные операции элементарного поглощения для элементарных конъюнкций длины [math] n-1[/math] (общая часть » [math]p[/math] » имеет длину [math] n-1[/math] )
- В результате получилось множество элементарных конъюнкций, разделяемых на два подмножества (по длине):
- подмножество элементарных конъюнкций длины [math] n[/math] (оставшиеся)
- подмножество элементарных конъюнкций длины [math] n-1[/math]
- Если множество элементарных конъюнкций длины [math] n-1[/math] не пусто, то заново выполняются операции неполного попарного склеивания и элементарного поглощения для конъюнкций длины [math] n-1[/math] и так далее.
Алгоритм завершается, когда подмножество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания. После выполнения этого алгоритма будет получена сокращенная (но еще не минимальная) форма.
Переход от сокращённой формы к минимальной осуществляется с помощью специальной таблицы. Члены СДНФ заданной функции вписываются в столбцы, а в строки — члены сокращённой формы. Отмечаются столбцы членов СДНФ, которые поглощаются отдельными элементами сокращённой формы.
Члены сокращённой формы, не подлежащие исключению, образуют ядро. Такие члены определяются по вышеуказанной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только этим членом.
Для получения минимальной формы достаточно выбрать из членов сокращённой формы, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждом из этих членов, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра.
Пример [ править ]
Функция от четырёх аргументов задана следующей таблицей:
Проведём операции неполного склеивания и поглощения:
| № | Элементарная конъюнкция | Поглощение |
|---|---|---|
| [math]1[/math] | [math]\neg x\neg y\neg z\neg w[/math] | [math]+[/math] |
| [math]2[/math] | [math]\neg xy\neg z\neg w[/math] | [math]+[/math] |
| [math]3[/math] | [math] x\neg yz\neg w[/math] | [math]+[/math] |
| [math]4[/math] | [math] x\neg y zw[/math] | [math]+[/math] |
| [math]5[/math] | [math] xy\neg z\neg w[/math] | [math]+[/math] |
| [math]6[/math] | [math] xy\neg zw[/math] | [math]+[/math] |
| [math]7[/math] | [math] xyz\neg w[/math] | [math]+[/math] |
| [math]8[/math] | [math] xyzw[/math] | [math]+[/math] |
| № склеивания | Результат |
|---|---|
| [math]1 — 2[/math] | [math]\neg x \neg z\neg w[/math] |
| [math]2 — 5[/math] | [math]y \neg z\neg w[/math] |
| [math]3-4[/math] | [math] x \neg yz[/math] |
| [math]3-7[/math] | [math] \neg x \neg z\neg w[/math] |
| [math]4-8[/math] | [math] xzw[/math] |
| [math]5-6[/math] | [math] xy\neg z[/math] |
| [math]5-7[/math] | [math] xy \neg w[/math] |
| [math]6-8[/math] | [math] xyw[/math] |
| [math]7-8[/math] | [math] xyz[/math] |
На данном шаге все элементы вида [math]Ax[/math] или [math]A \neg x[/math] участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому элементы сокращённой ДНФ на этом шаге не получены.
| № | Элементарная конъюнкция | Поглощение |
|---|---|---|
| [math]1[/math] | [math]\neg x\neg z\neg w[/math] | |
| [math]2[/math] | [math]y\neg z\neg w[/math] | |
| [math]3[/math] | [math] x\neg yz[/math] | [math]+[/math] |
| [math]4[/math] | [math] \neg x\neg z\neg w[/math] | [math]+[/math] |
| [math]5[/math] | [math] xzw[/math] | [math]+[/math] |
| [math]6[/math] | [math] xy\neg z[/math] | [math]+[/math] |
| [math]7[/math] | [math] xy\neg w[/math] | [math]+[/math] |
| [math]8[/math] | [math] xyw[/math] | [math]+[/math] |
| [math]9[/math] | [math] xyz[/math] | [math]+[/math] |
| № склеивания | Результат |
|---|---|
| [math]3-9[/math] | [math]xz[/math] |
| [math]4 — 5[/math] | [math]xz[/math] |
| [math]6-9[/math] | [math] xy[/math] |
| [math]7-8[/math] | [math] xy[/math] |
На данном этапе получаем элементы сокращённой ДНФ [math]\neg x \land \neg z \land \neg w[/math] и [math]y \land \neg z \land \neg w[/math]
| № | Элементарная конъюнкция | Поглощение |
|---|---|---|
| [math]1[/math] | [math]xz[/math] | |
| [math]2[/math] | [math]xy[/math] |
Обе элементарные конъюнкции на данном шаге являются элементами сокращённой ДНФ.
В результате выполнения алгоритма мы получаем следующую сокращённую ДНФ: [math](\neg x \land \neg z \land \neg w) \lor (y \land \neg z \land \neg w) \lor (x \land z) \lor (x \land y) [/math]
Переход от сокращённой формы к минимальной:
- Единицы ДНФ, покрываемые элементами [math]Ax[/math] или [math]A \neg x[/math] обозначаются «+». Пары [math]Ax[/math] и [math]A \neg x[/math] , попадающие в ядро помечаются «*».
- Единицы функции, которые покрываются только каким-то одним конъюнктом из системы элементов сокращённой ДНФ, помечаются “>”.
- Единицы функции, покрываемые ядром, но не покрываемые только каким-то одним конъюнктом из системы элементов сокращённой ДНФ помечаются “>>”.
| [math]\neg x\neg y\neg z\neg w[/math] [math]\gt [/math] | [math]\neg x y\neg z\neg w[/math] [math]\gt \gt [/math] | [math]x\neg yz\neg w[/math] [math]\gt [/math] | [math]x\neg yzw[/math] [math]\gt [/math] | [math]xy\neg z\neg w[/math] [math]\gt \gt [/math] | [math]xy\neg zw[/math] [math]\gt [/math] | [math]xyz\neg w[/math] [math]\gt \gt [/math] | [math]xyzw[/math] [math]\gt \gt [/math] |
|---|---|---|---|---|---|---|---|
| [math]\neg x\neg z\neg w^*[/math] | [math]+[/math] | [math]+[/math] | |||||
| [math]y\neg z\neg w[/math] | [math]+[/math] | [math]+[/math] | |||||
| [math]xz^*[/math] | [math]+[/math] | [math]+[/math] | [math]+[/math] | [math]+[/math] | |||
| [math]xy^*[/math] | [math]+[/math] | [math]+[/math] | [math]+[/math] | [math]+[/math] |
На основе этой таблицы получим ядро [math](\neg x \land \neg z \land \neg w) \lor (x \land z) \lor (x \land y) [/math] , которое является также и минимальной ДНФ.
Источник