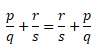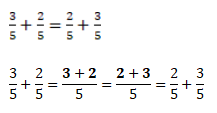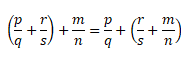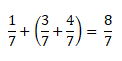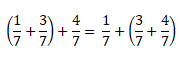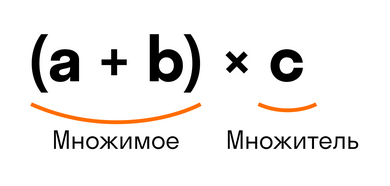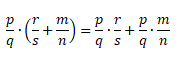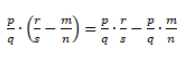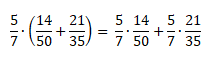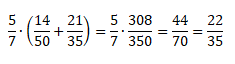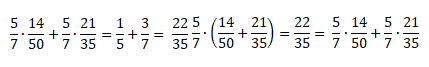Сочетательный способ сложения 5 класс

Сложение. Свойства переместительного и сочетательного законов.

Сложение натуральных чисел.

Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц.
Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.

Сумма — это сложение чисел. Знак плюс “+”.
В буквенном виде этот пример будет выглядеть так:

a+b=c

Компоненты сложения:
a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.

Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:

4+3=3+4

Называется такое свойство слагаемых переместительным законом сложения.

Переместительный закон сложения.

От перемены мест слагаемых сумма не меняется.

В буквенной записи переместительный закон выглядит так:

a+b=b+a

Если мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 4. И выполним сложение в таком порядке, сначала прибавим 1+2, а потом выполним сложение к получившейся сумме 4, то получим выражение:

(1+2)+4=7

Можем сделать наоборот, сначала сложить 2+4, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так:

1+(2+4)=7

Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод:

(1+2)+4=1+(2+4)

Это свойство сложения называется сочетательным законом сложения.

Переместительный и сочетательный закон сложения работает для всех неотрицательных чисел.

Сочетательный закон сложения.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.

(a+b)+c=a+(b+c)

Сочетательный закон работает для любого количества слагаемых. Этот закон мы используем, когда нам нужно сложить числа в удобном нам порядке. Например, сложим три числа 12, 6, 8 и 4. Удобнее будет сначала сложить 12 и 8, а потом прибавить к полученной сумме сумму двух чисел 6 и 4.
(12+8)+(6+4)=30

Свойство сложения с нулем.

При сложении числа с нулем, в результате сумма будет тем же самым числом.

В буквенном выражение сложение с нулем будет выглядеть так:

a+0=a
0+a=a

Вопросы по теме сложение натуральных чисел:
Таблица сложения, составьте и посмотрите как работает свойство переместительного закона?
Таблица сложения от 1 до 10 может выглядеть так:

Второй вариант таблицы сложения.

Если посмотрим на таблицы сложения, видно как работает переместительный закон.

В выражении a+b=c суммой, что будет являться?
Ответ: сумма — это результат сложения слагаемых. a+b и с.

В выражении a+b=c слагаемыми, что будет являться?
Ответ: a и b. Слагаемые – это числа, которые мы складываем.

Что произойдет с числом если к нему прибавить 0?
Ответ: ничего, число не поменяется. При сложении с нулем, число остается прежнем, потому что нуль это отсутствие единиц.

Сколько слагаемых должно быть в примере, чтобы было можно применить сочетательный закон сложения?
Ответ: от трех слагаемых и больше.

Запишите переместительный закон в буквенном выражении?
Ответ: a+b=b+a

Примеры на задачи.
Пример №1:
Запишите ответ у представленных выражений: а) 15+7 б) 7+15
Ответ: а) 22 б) 22

Пример №2:
Примените сочетательный закон к слагаемым: 1+3+5+2+9
1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Ответ: 20.

Пример №3:
Решите выражение:
а) 5921+0 б) 0+5921
Решение:
а) 5921+0 =5921
б) 0+5921=5921

Источник

Законы математики

О чем эта статья:

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:

m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

Формула переместительного закона для обыкновенных дробей:

Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа

1. Результат сложения нескольких слагаемых не зависит от порядка действий.
2. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

• 1 + 3 + 4 = (1 + 3) + 4 = 5 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

• 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.

Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.

Значит, сочетательный закон справедлив и для обыкновенных дробей.

Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения

От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

Переместительный закон умножения с помощью переменных выглядит так:

a * b = b * a

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения

Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.

Другими словами, умножайте числа в любом порядке — как вам больше нравится.

Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

• 3 * 4 = 12
• 2 * 12 = 24
• 2 * 3 * 4 = 24

Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.

• (2 * 3) * 4 = 2 * (3 * 4)
• 6 * 4 = 2 * 12
• 24 = 24

Для любых натуральных чисел a, b и c верно равенство:

a * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Это выражение можно вычислять в любом порядке. Вычислим слева направо:

5 * 6 * 7 * 8 = 1680

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения

• Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
• Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:

Сначала выполним действие в скобках:

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

• (3 + 5) * 2 = 3 * 2 + 5 * 2
• 3 * 2 = 6
• 5 * 2 = 10
• 6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.

Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:

c * (a + b) = c * a + c * b

Пример 1

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Пример 2

Найти значение выражения 2 * (5 + 2).

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.

Пример 3

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Распределительный закон умножения для суммы обыкновенных дробей:

Распределительный закон умножения для разности обыкновенных дробей:

Проверим справедливость этого закона:

Посчитаем, чему равна левая часть равенства.

Теперь посчитаем, чему равна правая часть равенства.

Так мы доказали справедливость распределительного закона.

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)

Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?

Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?

Задание 8. Верно ли равенство: 8 * 5 = 49?

Источник