Сочетание m элементов n способами

2.1. Основные комбинаторные формулы

Размещения. Размещениями из N элементов по M в каждом называются такие соединения, из которых каждое содержит M элементов, взятых из числа данных N элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.

Число размещений из N элементов по M в каждом обозначается символом И вычисляется по формуле

, (1)

Где (считается, что 0! = 1).

Пример 2.1. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?

Решение. В этом случае надо найти число размещений (без повторений) из 25 элементов по 4, так как здесь играет роль и то, кто будет выбран в руковод­ство общества, и то, какие посты займут выбранные.

Ответ: .

Размещения с повторениями. Каждое размещение с повторениями из
N элементов по M элементов может состоять не только из различных элементов, но из M каких угодно и как угодно повторяющихся элементов, взятых из данных N элементов.

Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.

Число размещений с повторениями из n элементов по M элементов обозначается символом и вычисляется по формуле

(2)

Пример 2.2. Для запирания сейфов и автоматических камер хранения применяют секретные замки, которые открываются лишь тогда, когда набрано некоторое «тайное слово». Пусть на диск нанесено 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова?

Решение. Общее число возможных комбинаций можно найти по формуле (2)

.

Число неудачных попыток — 248 832 – 1 = 248 831.

Сочетания. Сочетаниями из N элементов по M в каждом называются такие соединения, из которых каждое содержит M элементов, взятых из числа данных N элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Число сочетаний из n элементов по M в каждом обозначается символом и вычисляется по формуле

, (3)

Где .

Пример 2.3. Покупая карточку лотереи «Спортлото», игрок должен зачеркнуть 6 из 49 возможных чисел от 1 до 49. Сколько возможных комбинаций можно составить из 49 по 6, если порядок чисел безразличен?

Решение. Число возможных комбинаций можно рассчитать по формуле (3)

.

Сочетания с повторениями. Сочетание с повторениями из N элементов по M элементов может содержать любой элемент сколько угодно раз от 1 до M включительно или не содержать его совсем, т. е. каждое сочетание из N элементов по M элементов может состоять не только из M различных элементов, но из M каких угодно и как угодно повторяющихся элементов.

Число сочетаний с повторениями из n элементов по M обозначают символом и вычисляют по формуле

.

В сочетаниях с повторениями M может быть и больше N.

Пример 2.4. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение. Число различных покупок равно числу сочетаний с повторениями из 4 по 7:

.

Ответ: Из пирожных 4 сортов 7 пирожных можно выбрать 120 способами.

Перестановки. Перестановками из N элементов называются такие соединения, из которых каждое содержит все N элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Число перестановок из N элементов обозначается символом , это то же самое, что число размещений из N элементов по N в каждом, поэтому

.

Пример 2.5. Сколько существует способов составления списка 10 деловых звонков случайным образом?

Решение. Количество способов составления списка из 10 звонков будет равно числу перестановок из 10 элементов:

.

Ответ: Число способов составления списка из 10 звонков равно 3 628 800.

Перестановки с повторениями. Пусть имеются N элементов, среди которых элементов одного типа, элементов другого типа, элементов
L-го типа . Число перестановок из этих N элементов равно числу перестановок с повторениями, обозначается и вычисляется по формуле

.

Пример 2.6. Десять приезжих мужчин размещаются в гостинице в двух трехместных и одном четырехместном номерах. Сколько существует способов их размещения?

Решение.

Источник

Сочетания из n элементов по m

Элементы математической статистики.

Основные понятия и термины: комбинаторика, элементы комбинаторики, перестановка, факториал, сочетания, размещения

Комбинато́рика— раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов.

Пусть имеется n различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно P_n=n!=1⋅2⋅3⋅. ⋅(n−1)⋅n

Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению, считают, что 0!=1,1!=1

Множество n=3 элементов Перестановки (всего P₃=3!=1⋅2⋅3=6)

Число всех перестановок порядка n равно факториалу: P_n=n!

Факториа́лчисла n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно.

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел. Например,

С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов – уже 3 628 800(больше 3 миллионов!).

Задача.Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?

На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 • 3 • 2 • 1 = 4!.

Задача.На танцплощадке собрались 7 юношей и 7 девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце? (выбрать 7 пар)

Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

Задача. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?

Решение. Перечислим все возможные варианты:

Используя правило умножения, получаем: 5х3=15 (с нуля число не может начинаться, поэтому 5, четные цифры 0,2,6)

Задача. Имеется три класса учеников. В первом классе 15 человек, во втором 17, в третьем -20. Нужно выбрать 3 ученика из каждого класса. Сколькими способами можно это сделать?

Решение: Из первого класса выбираем ученика 15 способами, из второго 17 способами, из третьего -20 способами. Всего способов 15·17·20=5100

Задача. Имеются пять видов конвертов без марок и четыре вида марок. Сколькими способами можно выбрать конверт с маркой для посылки письма?

Сочетания из n элементов по m

Множество n=3 элементов Сочетания по 2 элемента

Пусть имеется n различных объектов. Будем выбирать из них m объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m, а их число равно

Пример всех сочетаний из n=3 объектов (различных фигур) по m=2- на картинке. Согласно формуле, их должно быть ровно

C 2 ₃=3!/2!(3−2)! =3. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний — нет), причем именно в m! раз.

Задача. Сколько экзаменационных комиссий, состоящих из 3 членов, можно образовать из 10 преподавателей?

Решение: По формуле находим:

= 120 комиссий

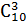
Источник

Сочетание m элементов n способами

1. Элементы комбинаторики.

2. Общие правила комбинаторики.

3. Генеральная совокупность без повторений и выборки без повторений.

4. Применение графов (схем) при решении комбинаторных задач.

1. Комбинаторика и ее возникновение.

Комбинаторика— это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.

Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры (карты, кости). Широко были распространены лотереи. Первоначально комбинаторные задачи касались в основном азартных игр: сколькими способами можно получить данное число очков, бросая 2 или 3 кости или сколькими способами можно получить 2-ух королей в некоторой карточной игре. Эти и другие проблемы азартных игр являлись движущей силой в развитии комбинаторики и далее в развитии теории вероятностей.

Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицы (числа способов выпадения k очков на r костях). Однако, он не учел, одна и та же сумма очков может выпасть различными способами, поэтому его таблицы содержали большое количество ошибок.

Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские математики Блез Паскаль и Ферма. Исходным пунктом их исследований были так же проблемы азартных игр.

Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г. Лейбница, Л. Эйлера. Однако, и в их работах основную роль играли приложения к различным играм.

Сегодня комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции и т.д.

2. Общие правила комбинаторики.

Правило суммы: Если некоторый объект А может быть выбран m способами, а объект В- k способами, то объект «либо А, либо В» можно выбрать m + k способами.

1. Допустим, что в ящике находится n разноцветных шаров. Произвольным образом вынимается 1 шарик. Сколькими способами это можно сделать?

Распределим эти n шариков по двум ящикам: в первый- m шариков, во второй- k шариков. Произвольным образом из произвольно выбранного ящика вынимается 1 шарик. Сколькими способами это можно сделать?

Решение: Из первого ящика шарик можно вынуть m способами, из второго- k способами. Тогда всего способов m+k=n .

В морском семафоре каждой букве алфавита соответствует определенное положение относительно тела сигнальщика двух флажков. Сколько таких сигналов может быть?

Решение: Общее число складывается из положений, когда оба флажка расположены по разные стороны от тела сигнальщика и положений, когда они расположены по одну сторону от тела сигнальщика. При подсчете числа возможных положений применяется правило суммы.

Правило произведения: Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) k способами, то пары объектов «А и В» можно выбрать m *k способами.

1. Сколько двузначных чисел существует?

Решение: Число десятков может быть обозначено любой цифрой от 1 до 9. Число единиц может быть обозначено любой цифрой от 0 до 9. Если число десятков равно 1, то число единиц может быть любым (от 0 до 9). Таким образом, существует 10 двузначных чисел, с числом десятков- 1. Аналогично рассуждаем и для любого другого числа десятков. Тогда можно посчитать, что существует 9 *10 = 90 двузначных чисел.

2. Имеется 2 ящика. В одном лежит m разноцветных кубиков, а в другом- k разноцветных шариков. Сколькими способами можно выбрать пару «Кубик-шарик»?

Решение: Выбор шарика не зависит от выбора кубика, и наоборот. Поэтому, число способов, которыми можно выбрать данную пару равно m *k .

3. Генеральная совокупность без повторений и выборки без повторений.

Генеральная совокупность без повторений— это набор некоторого конечного числа различных элементов a₁ , a₂, a₃, . a_n.

Пример: Набор из n разноцветных лоскутков.

Выборкой объема k ( k n ) называется группа из m элементов данной генеральной совокупности.

Пример: Пестрая лента, сшитая из m разноцветных лоскутков, выбранных из данных n .

Размещениями из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга либо составом элементов, либо порядком их расположения.

— число размещений из n по k .

Число размещений из n по k можно определить следующим способом: первый объект выборки можно выбрать n способами, далее второй объект можно выбрать n -1 способом и т.д.

Преобразовав данную формулу, имеем:

Следует помнить, что 0!=1.

1. В первой группе класса А первенства по футболу участвует 17 команд. Разыгрываются медали: золото, серебро и бронза. Сколькими способами они могут быть разыграны?

Решение: Комбинации команд-победителей отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 17 по 3.

2. Научное общество состоит из 25-ти человек. Необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами это можно сделать?

Решение: Комбинации руководящего состава общества отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 25 по 4.

Перестановками без повторений из n элементов называются размещения без повторений из n элементов по n , т.е. размещения отличаются друг от друга только порядком следования элементов.

1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что они должны состоять из различных цифр?

Решение: Имеем перестановки из 5 элементов.

Сочетаниями без повторений из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга только составом элементов.

— число сочетаний из n по k

Элементы каждого из сочетаний можно расставить способами. Тогда

1. Если в полуфинале первенства по шахматам участвует 20 человек, а в финал выходят лишь трое, то сколькими способам и можно определить эту тройку?

Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки, вышедшие в финал, являются сочетаниями из 20 по 3.

Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки делегатов являются сочетаниями из 10 по 3.

4. Применение графов (схем) при решении комбинаторных задач.

В случае, когда число возможных выборов на каждом шагу зависит от того, какие элементы были выбраны ранее, можно изобразить процесс составления комбинаций в виде «дерева». Сначала из одной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу. Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если на первом шагу был выбран данный элемент и т.д.

При составлении команд космического корабля учитывается вопрос и психологической совместимости участников путешествия. Необходимо составить команду космического корабля из 3 человек: командира, инженера и врача. На место командира есть 4 кандидата: a₁, a₂, a₃, a₄ . На место инженера- 3: b₁, b₂, b₃. На место врача- 3: c₁, c₂, c₃ . Проведенная проверка показала, что командир a₁ психологически совместим с инженерами b₁ и b₃ и врачами c ₁ и c₃ . Командир a₂ — с инженерами b₁ и b₂. и всеми врачами. Командир a₃ — с инженерами b₁ и b₂ и врачами c ₁ и c₃ . Командир a₄-со всеми инженерами и врачом c₂. Кроме того, инженер b₁ не совместим с врачом c₃ , b₂— с врачом c₁ и b₃— с врачом c₂. Сколькими способами при этих условиях может быть составлена команда корабля?

Составим соответствующее «дерево».

Ответ: 10 комбинаций.

Такое дерево является графом и применяется для решения комбинаторных задач.

Источник