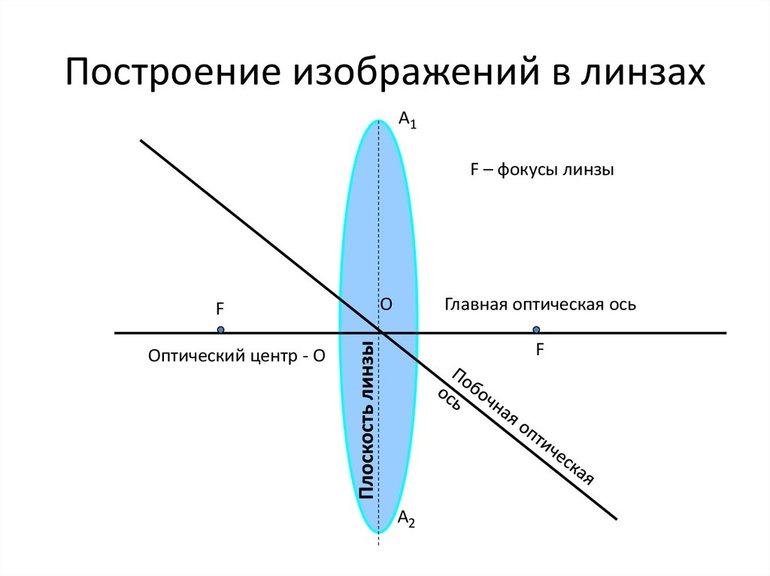
Построение в линзах
Для введённых нами линз существует два условно разных типа задач:
- задачи на построение в собирающей и рассеивающей линзах
- задачи на формулу для тонкой линзы
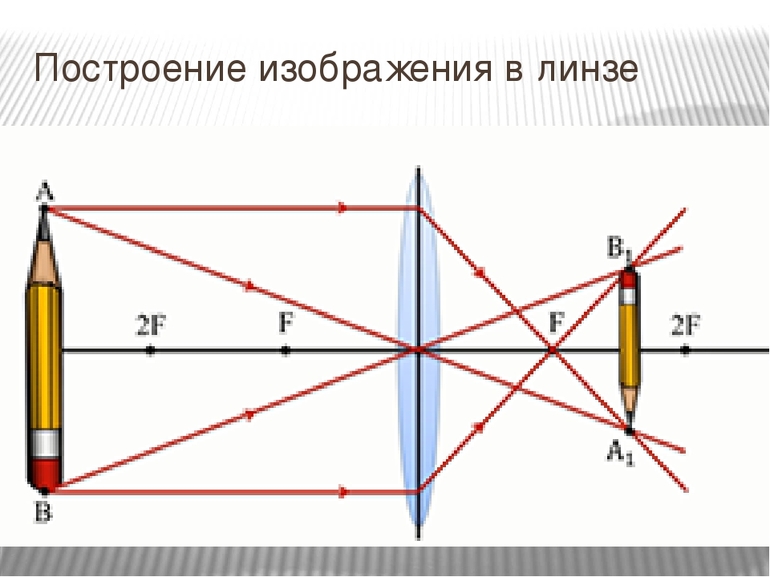
Первый тип задач основан на фактическом построении хода лучей от источника и поиска пересечения преломлённых в линзах лучей. Рассмотрим ряд изображений, полученных от точечного источника, который будем помещать на различных расстояниях от линз. Для собирающей и рассеивающей линзу существуют рассмотренные (не нами) траектории распространения луча (рис. 1) от источника .
Рис.1. Собирающая и рассеивающая линзы (ход лучей)
Для собирающей линзы (рис. 1.1) лучи:
- синий. Луч, идущий вдоль главной оптической оси, после преломления проходит через передний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
- красный. Луч, идущий через передний фокус, после преломления распространяется параллельно главной оптической оси.
Пересечение любых из этих двух лучей (чаще всего выбирают лучи 1 и 2) дают изображение ( ).
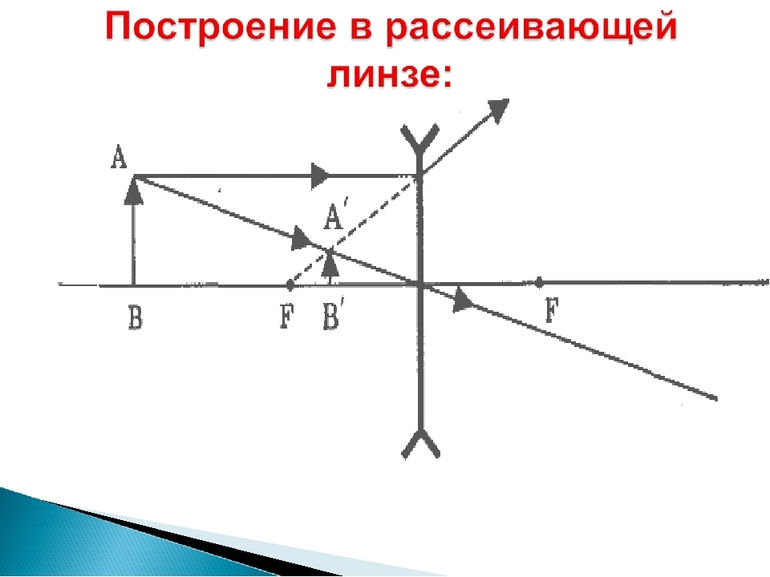
Для рассеивающей линзы (рис. 1.2) лучи:
- синий. Луч, идущий параллельно главной оптической оси, преломляется так, что продолжения луча проходит через задний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
Пересечение продолжений рассмотренных лучей даёт изображение ( ).
Аналогично сферическому зеркалу, получим набор изображений от предмета, расположенного на различных расстояниях от зеркала. Введём те же обозначения: пусть — расстояние от предмета до линзы, — расстояние от изображения до линзы, — фокусное расстояние (расстояние от фокуса до линзы).
Для собирающей линзы:
- (источник находится очень далеко от линзы). В этом случае мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 2). Пустим два луча параллельно главной оптической оси линзы.
Рис. 2. Собирающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе проходят через фокус, то точка фокуса и является точкой пересечения преломлённых лучей, тогда она же и есть изображение источника (точечное, действительное).
- 2F» title=»\displaystyle d>2F» data-lazy-src=»https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+d%3E2F&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=»data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″> (источник находится за двойным фокусным расстоянием) (рис. 3).
Рис. 3. Собирающая линза (источник за двойным фокусом)
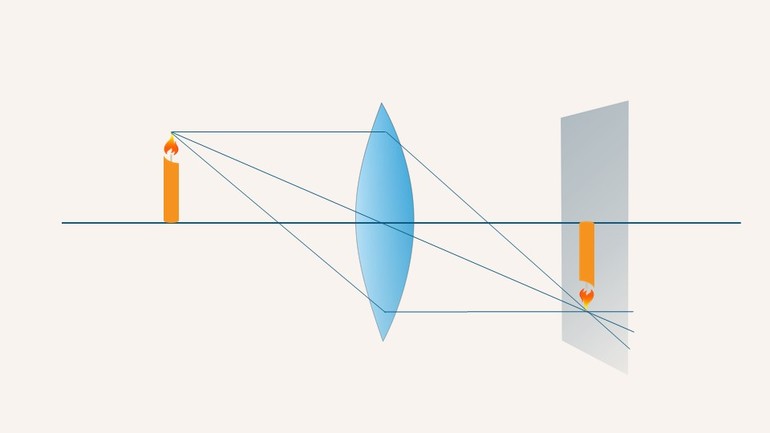
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Для визуализации изображения введём описание предмета через стрелку. Точка пересечения преломившихся лучей — изображение (уменьшенное, действительное, перевёрнутое). Положение — между фокусом и двойным фокусом.
- (источник находится ровно в двойном фокусе) (рис. 4).
Рис. 4. Собирающая линза (источник в двойном фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (того же размера, действительное, перевёрнутое). Положение — ровно в двойном фокусе.
- d>F» title=»\displaystyle 2F>d>F» data-lazy-src=»https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+2F%3Ed%3EF&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=»data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″> (источник между фокусом и двойным фокусом) (рис. 5)
Рис. 5. Собирающая линза (источник между двойным фокусом и фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (увеличенное, действительное, перевёрнутое). Положение — за двойным фокусом.
- (источник находится ровно в фокусе собирающей линзы) (рис. 6)
Рис. 6. Собирающая линза (источник в фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). В этом случае, оба преломлённых луча оказались параллельными друг другу, т.е. точка пересечения отражённых лучей отсутствует. Это говорит о том, что изображения нет.
- (источник находится между фокусом и главным оптическим центром) (рис. 7)
Рис. 7. Собирающая линза (источник перед фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Однако преломлённые лучи расходятся, т.е. сами преломлённые лучи не пересекутся, зато могут пересечься продолжения этих лучей. Точка пересечения продолжений преломлённых лучей — изображение (увеличенное, мнимое, прямое). Положение — по ту же сторону, что и предмет.
Для рассеивающей линзы построение изображений предметов практически не зависит от положения предмета, так что ограничимся произвольным положением самого предмета и характеристикой изображения.
- (источник находится очень далеко от линзы). В этом случае, мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 8). Пустим два луча параллельно главной оптической оси линзы.
Рис. 8. Рассеивающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе должны проходить через фокус (свойство фокуса), однако после преломления в рассеивающей линзе лучи должны расходится. Тогда в фокусе сходятся продолжения преломившихся лучей. Тогда точка фокуса и является точкой пересечения продолжений преломлённых лучей, т.е. она же и есть изображение источника (точечное, мнимое).
- любое другое положение источника (рис. 9).
Рис. 9. Рассеивающая линза (произвольное положение источника)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (продолжение отражённого луча проходит через передний фокус) и идущего через главный оптический центр линзы (не преломляется). Тогда изображением будет пересечение продолжений преломлённых лучей.
Второй тип задач связан с формулой тонкой линзы. Такие задачи основываются на числовых данных параметров, характеризующих положение источника, изображения или фокуса линзы. Рассмотрим произвольную систему (рис. 10). Пусть положение источника ( ), изображения ( ) и фокуса системы ( ) задано.
Рис. 10. Формула тонкой линзы
Тогда взаимосвязь между параметрами положения элементов можно описать формулой:
- где
- — фокусное расстояние линзы,
- — расстояние от предмета до линзы,
- — расстояние от изображения до линзы.
Важно: для использования формулы (1) необходимо помнить правило расстановки знаков. Если линза собирающая, то 0″ title=»\displaystyle F>0″ data-lazy-src=»https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+F%3E0&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=»data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″>, если рассеивающая, то . В случае действительных предметов и изображений: 0″ title=»\displaystyle d>0″ data-lazy-src=»https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+d%3E0&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=»data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″>, 0″ title=»\displaystyle f>0″ data-lazy-src=»https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%3E0&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=»data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″>, а в случае мнимых предметов и изображений: и .
И последним параметром, характеризующим линзы или систему линз, является оптическая сила линзы ( ). Её нахождение довольно простое:
- где
- — оптическая сила линзы/системы линз,
- — фокус линзы/системы линз.
Размерность оптической силы линзы: м =дптр (диоптрии). Оптическая сила собирающей линзы положительна, рассеивающей — отрицательна.
Вывод: задачи с линзами, в целом, разделены на два класса. Задачи на построение основываются на рисунках 2-9. Достаточно проанализировать ход лучей и найти изображение (рис.1). Численные значения в дано указывают на задачи на формулу тонкой линзы (1).
Источник
Построение изображений в линзах — виды, правила и формулы
В современной физике и оптике чаще применяются асферические предметы с отличной от сферы формой поверхности.
Материалы для их изготовления — кристаллы, стёкла, оптическая пластмасса. Для построения изображений в линзах потребуется выполнить чертеж на плоскости.
Принципы классификации
Понятие применяется к другим оптическим приборам и явлениям, которые изучаются на уроках физики в 11 классе. Подобное действие наблюдается в плоских линзах. При их изготовлении применяется материал с переменным показателем преломления. Он изменяется с учётом расстояния от центра. В зонной пластинке Френкеля используется явление дифракции (отклонение пучка света от прямолинейного распространения вблизи препятствия).
Воспринимаемая картинка считается действительной. Предусмотрено подобное построение изображения в собирающей линзе. Мнимые аналоги образуются расходящимися пучками. Их лучи не пересекаются в геометрической системе координат. Действительное и мнимое изображение может давать собирающее зеркало. Рассеивающий аналог создаёт мнимую картинку.
Главные и общие характеристики изделий:
- оптическая сила;
- фокусное расстояние.
Некоторые оптические системы фокального, фокусного, выпуклого видов используются в среде с относительно высоким показателем преломления.
Отличительное свойство собирательной лампочки — соединение падающих прямых в одной точке. Её можно править к изделию любой стороной.
Вывод — свет, проходя через экран с зеркалами, собирается с двух сторон от прибора.
Для изделия характерны 2 фокуса:
Они находятся на оптической оси с двух сторон и на фокусном расстоянии от главной точки. В ходе падения лучей на рассеивающую линзу и выхода из неё свет преломляется рассеиваясь. В технике используются лупы, обозначающие 2x, 3x. Чтобы увеличить картинку, используется формула:
Ud=F+d/F, где F — расстояние, d — расстояние наилучшего зрения.
Собирающие приборы
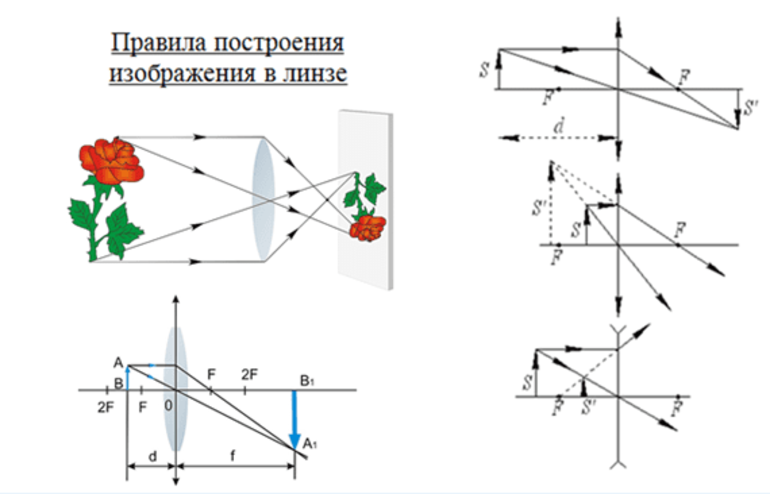
При построении изображения в собирающей линзе и расположении предмета за двойным фокусом необходимо опустить 2 луча. На стекле происходит преломление луча с последующим его прохождением через фокус. Другой луч направляется из верхней точки предмета через центр. Он проходит без кривизны, не преломляясь. При пересечении прямых образуется верхняя точка предмета.
По аналогичной схеме строится картинка нижней точки изделия. При таком построении получается перевёрнутое, уменьшенное и действительное фото.
Чтобы построить картинку, когда предмет находится в точке двойного фокуса, понадобятся 2 луча:
- Первый преломляется, пропускаясь через фокус.
- Второй направляется из верхней части через оптику. Он не преломляется.
На их пересечении ставится точка, с помощью которой получится картинка верхней части предмета. По аналогичной схеме строится чертёж нижних точек. Таким способом получается картинка с высотой, равной высоте самого изделия.
При расположении предмета в пространстве один луч проходит параллельно основной оси, а второй направляется через центр. В основе проекционного аппарата находится основное свойство собирающих линз: в процессе приближения изделия к линзе изменяются параметры фото.
Сложнее выполнить чертёж, используя светящуюся точку, расположенную на основной оптической оси. Для построения точки используется луч, направленный произвольно на линзу. В месте пересечения плоскости и побочной оси формируется другой фокус. В данную точку пойдёт преломлённая прямая после самой линзы. При построении изображения в рассеивающей линзе происходит преломление так, что продолжение прямой идёт в фокус. Вторая прямая попадает в центр, пересекая продолжение первой. На основе такого закона преломления получается картинка мнимая, прямая и уменьшенная.
Практические задания
Для рассматриваемых устройств существуют следующие типы задач: на построение в рассеивающей линзе либо собирающей, формула для тонкой поверхности.
Для решения первой потребуется построить ход луча от источника, отыскать пересечение преломленных прямых.
Если дана собирающая линза, луч имеет следующие цвета:
- Синий. Идёт вдоль основной оси, а после преломления поступает в фокус.
- Зелёный. Проходит сквозь оптический центр, без преломления.
- Красный. Проходя через фокус, преломляясь, распространяется параллельно основной оси.
При их пересечении получается соответствующее изображение. В рассеивающих линзах используются лучи синего, зелёного оттенков. Первый параллелен главной прямой, преломляется. Зелёный идёт сквозь оптическую центральную точку, не испытывая преломления. Лучам свойственно пересекаться, выдавая картинку.
Как и сферическое зеркало, можно получить несколько картинок от предмета, находящегося на разных расстояниях (d). Предположим, что длина отрезка от фото до линзы обозначается через f, а от фокуса до линзы через F.
При собирающей линзе значение первого показателя d будет стремиться к бесконечности. Источник расположен вдали от зеркала. Лучи расположены параллельно относительно друг друга.
Если пустить 2 прямые параллельно основной оси, тогда, преломляясь, они пройдут через фокус. Он является точечным изображением.
Различные значения показателей
Если d больше 2°F, источник расположен за фокусным отрезком. Чтобы визуализировать картинку, предмет описывается через стрелку. В точке скрещения лучей появляется изображение. Когда d= 2°F, источник размещён в фокусе. Если d больше F, но меньше 2°F, тогда источник находится между двойным и одинарным фокусом. При отсутствии побочных предметов, размещении зеркала с учётом расстояния d=F, когда источник совпадает с фокусом.
Если линза рассеивающая, при построении не учитывается положение предмета. В таком случае нужно ограничиваться его произвольным размещением и характеристиками фото. Если d приближается к бесконечности, тогда лучи идут от источника параллельно относительно друг друга.
После преломления они расходятся, а в фокусе их продолжения сходятся. Точки пересечения и фокуса совпадают. Таким способом получается мнимая картинка.
Другой тип заданий связан с формулой тоненькой линзы. Они основаны на числовых параметрах, с помощью которых характеризуется положение источника, фокуса либо картинки.
Если рассмотреть произвольную систему, тогда за положение источника можно взять d, а за фото — f. Фокусная система задается через F.
Взаимосвязь между всеми параметрами, которые используются при построении изображений в тонких линзах, описывается с помощью следующей формулы:
- F — расстояние фокусное;
- d — расстояние между зеркалом и предметом;
- f — отрезок между зеркалом и картинкой.
Чтобы воспользоваться формулой, нужно учитывать правило постановки знаков. Если прибор собирающий, тогда F больше нуля, а если рассеивающий, то меньше. Когда предметы и картинки действительные, тогда d>0, f=0.
Источник