Смешанный способ решения задач это

Содержание

Решение задач различными методами и способами
Содержимое разработки
Статья на тему: «Методы и способы решения текстовых задач»

Решение задач различными методами и способами

Презентация содержит приёмы работы над задачами на уроках математики в начальной школе

Содержимое разработки

Решение задач различными методами и способами

Куличенко Валентина Геннадьевна

«Славгородский педагогический колледж»

Умение решать задачу различными способами связывается с развитием гибкости мышления и играет определенную роль в развитии умственных способностей и математического мышления.

Обучение решению задач различными способами способствует более глубокому осознанию задачной ситуации, пониманию взаимосвязей между величинами, входящими в задачу, между данными и искомыми, развивает наблюдательность и математическую зоркость.

В методической литературе отмечается, что решение задачи различными способами часто бывает более полезным, чем решение одним способом нескольких задач.

При оценке разных способов решения активно используются такие умственные операции, как анализ,

что оказывает положительное влияние на развитие умственных способностей учащихся.

Методы решения задач

арифметический;
алгебраический ;
графический ;
практический ;
табличный ;
логический ;
смешанный.

основан на выборе арифметических действий, обусловленном различными связями и зависимостями между величинами, входящими в задачу, между данными и искомыми.

Задача 1. Для похода туристы закупили 96 банок консервов. В день они расходовали по 8 банок. Сколько банок консервов у них осталось после 10 дней?

Расходовали – 10 дн. по 8 б.

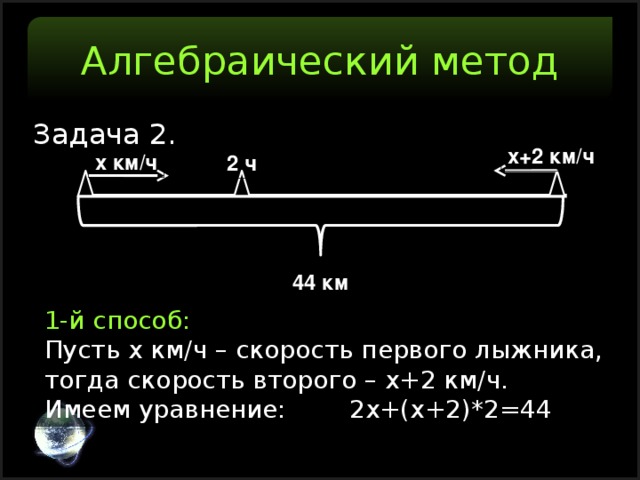
Задача 2. Из двух пунктов одновременно навстречу друг другу вышли два лыжника и через 2 ч встретились. Найдите скорость каждого лыжника, если расстояние между пунктами было 44 км, а скорость одного больше скорости другого на 2 км/ч.

Пусть х км/ч – скорость первого лыжника,

тогда скорость второго – х+2 км/ч.

Имеем уравнение: 2х+(х+2)*2=44

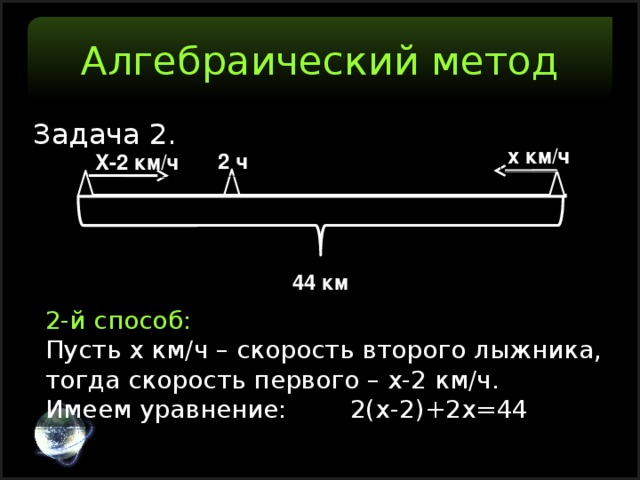
Пусть х км/ч – скорость второго лыжника,

тогда скорость первого – х-2 км/ч.

Имеем уравнение: 2(х-2)+2х=44

Задача 3. 8 яблок разложили на две тарелки. По скольку яблок на каждой тарелке?

Задача 4. Масса арбуза — 5 кг, а масса дыни на 2 кг меньше. Какова масса дыни?

Почти любую арифметическую задачу, которую решают в 1 классе, можно решить графически без выполнения арифметических действий. При этом учащиеся могут убедиться, что иногда этот подход к решению задач приводит к усложнению, а иногда позволяет легко и просто решить

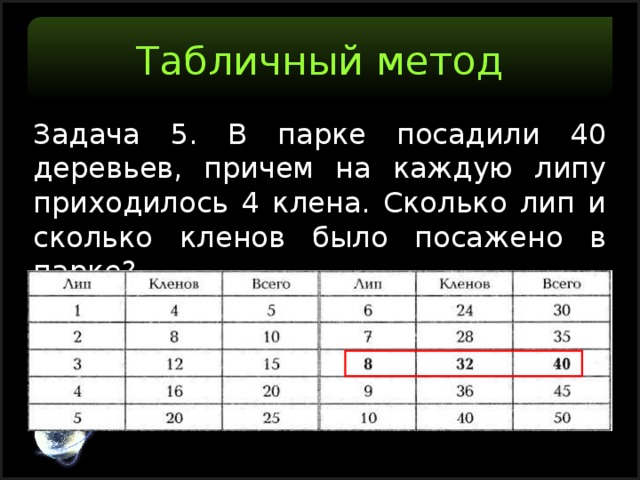
Задача 5. В парке посадили 40 деревьев, причем на каждую липу приходилось 4 клена. Сколько лип и сколько кленов было посажено в парке?

в процессе поиска решения на основе логических рассуждений можно дать ответ на вопрос задачи.

предполагает использование приемов работы по решению задач различными способами:

беседа, в процессе которой учитель подводит учащихся к тому или иному способу решения задачи;
обсуждение готовых решений — на доске учитель предлагает учащимся разные способы решения задачи и дает задание объяснить каждое выполняемое действие.

Задача 6. Рабочему было поручено изготовить 30 одинаковых деталей за 10 ч. Но рабочий, экономя время, успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени?

2) 600 — 450 = 150 (мин) —

60:15=4 (дет.) —
4-10=40 (дет.) —
40-30=10 (дет.) —

Источник

Статья на тему: «Методы и способы решения текстовых задач»

Методы и способы решения текстовых задач

Начну с того, что же такое задача. Ведь термин задача встречается нам как в быту, так и в профессии. Каждый из нас решает ежедневно те или иные задачи. Задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий. Текстовая задача – описание некоторой ситуации на естественном языке, с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами и определить вид этого отношения. Любая текстовая задача состоит из двух частей – условия и требования (вопроса). В условии соблюдаются сведения об объектах и некоторые числовые данные объекта, об известных и неизвестных значениях между ними. Требования задачи – это указание того, что нужно найти. Оно выражено предложением в повелительной или вопросительной форме. Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие должно быть выполнено для получения ответа на требование задачи. Ответ на требование задачи получается в результате ее решения. Решить задачу в широком смысле этого слова — это значит раскрыть связи между данными, заданными условием задачи, и искомыми величинами, определить последовательность применения общих положений математики (правил, законов, формул и т. д.), выполнить действия над данными задачи, используя общие положения и получить ответ на требование задачи или доказать невозможность его выполнения.
Прежде всего надо, осознать, что такое текстовая задача. И целью подготовительного периода является возможность показать перевод различных реальных явлений на язык математических символов и знаков. Также для того, чтобы правильно выбрать то или иное действие для решения простой задачи, необходимо сформировать понятие об арифметических действиях, научить выбирать то или иное действие. Решением задачи называют результат, т. е. ответ на требование задачи.

Текстовые задачи мы можем условно классифицировать по типам: задачи на числовые зависимости; задачи, связанные с понятием процента; задачи на «движение», «концентрацию смесей и сплавов», «работу» и т. д.

Решение текстовых задач делится на несколько этапов:

восприятие и осмысление задачи;

поиск плана решения;

выполнение плана решения;

Существуют различные методы решения текстовых задач:

метод проб и ошибок.

В основе каждого метода лежат различные виды математических моделей.

Например, при алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом — строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.

Следует иметь в виду, что практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Так, используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения, используя логический метод — построив разные алгоритмы. Ясно, что в этих случаях мы так же имеем дело с различными методами решения конкретной задачи, которые называю способы решения.

Арифметический метод. Решить задачу арифметическим методом — значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту де задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью этих связей.

Алгебраический метод . Решить задачу алгебраическим методом — это значит найти ответ на требование задачи, составив и решив уравнение или системы уравнений (или неравенств). Одну и ту же задачу можно так же решить различными алгебраическими способами. Задача считается решенной различными способами, если для ее решения составлены различные уравнения или системы уравнений (неравенств), в основе составления которых лежат различные соотношения между данными и искомыми.

Геометрический метод. Решить задачу геометрическим методом — значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.

Логический метод . Решить задачу логическим методом — это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.

Практический метод . Решить задачу практическим методом — значит найти ответ на требования задачи, выполнив практические действия с предметами или их копиями (моделями, макетами).

Табличный метод позволяет видеть задачу целиком это — решение путем занесения содержания задачи в соответствующим образом организованную таблицу.

Комбинированный метод позволяет получить ответ на требование задачи более простым путем.

Метод проб и ошибок (самый примитивный), в нем ответ на вопрос задачи угадывается. Но и здесь основные моменты решения — выбор пробных ответов на вопрос задачи и проверка их соответствия условию осуществляется с помощью мыслительных операций, необходимых при решении любым путем. Угадывание ответа требует интуиции, без которой невозможно никакое решение.

Методы решения могут быть разные, но способ решения, лежащий в их основе, может быть один.

Работа над текстовой задачей остается одним из важнейших аспектов обучения в начальной школе, когда закладываются основы знаний; является движущим фактором в развитии младших школьников. Из текстов задач дети открывают новое об окружающем мире, испытывают чувство удовлетворения и радости от их успешного решения.
Решение текстовых задач и нахождение разных способов их решения на уроках математики способствует развитию у детей мышления, памяти, внимания, творческого воображения, наблюдательности, последовательности рассуждения и его доказательности, развитию умения кратко, четко и правильно излагать свои мысли.

При решении любых текстовых задач на движение наиболее рационально принимать в качестве неизвестных величин расстояние, скорость или наименьшую из величин, что приводит к более короткому решению. Если после составления уравнений, полученная система не решается, то необходимо попробовать выбрать другие неизвестные. Количество неизвестных не имеет значения, правильное составление системы превыше всего. Также, нужно обращать особое внимание на единицы измерения – в течение всего решения они обязательно должны быть одинаковыми. А именно, если это часы, то на протяжении всей задачи время должно выражаться в часах, а не в минутах, так и, километры и метры не должны применяться в одном решении и т. п.

Для преобразования условия задачи в математическую модель математические знания практически не нужны – здесь необходим здравый смысл. Очень важно обязательно сформулировать, используя переменные, что мы обязаны найти, т. к. переменных может быть намного больше, чем уравнений, где все их найти просто невозможно.

Решая системы нужно помнить, что в текстовых задачах все величины, как правило, положительны, т. к. в природе отрицательных скоростей и расстояний не существует. Это даёт нам право на умножение, деление и на возведение в квадрат получающиеся уравнения и неравенства.

Решая задачи «на работу», очень выгодно принимать за неизвестные величины производительность (работа, производимая за единицу времени), но бывают и исключения, где необходимо за неизвестную, например, выбрать время. Иногда встречаются такие задачи, в которых не указывается, какая работа выполняется. В таких задачах, будет удобнее ввести самим единицу работы, равную всей работе. Во время исследования была обнаружена всего одна задача, где помимо рассмотрения деятельности всех рабочих, важно рассмотреть их совместную деятельность, а иначе задача будет решена не верно.

В задах «на производительность» стоит лишь отметить то, что за производительность трубы принимается объём жидкости, протекающей через неё за единицу времени. Также, бывают случаи, когда необходимо принять за неизвестные одновременно объём бассейна, производительность труб и время наполнения бассейна каждой трубой, чего не стоит опасаться.

Источник