6.3.4. Начисление процентов за дробное число лет
Довольно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться одним из двух методов:
- по схеме сложных процентов
Поскольку 
, следовательно, наращенная сумма будет больше при использовании смешанной схемы. Можно показать, что при малых г наибольшая величина разности между (6.12) и (6,11) достигается при ƒ ≈ 0,5.
Пример
Банк предоставил кредит в размере 10 млн руб. на 30 мес. под 30% годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока?
Решение
По формуле (6.11): FV n =10 • (1 + 0,3) 2+0,5 = 19,269 млн руб.
По формуле (6.12): FV n = 10 • (1 + 0,3) 2 • (1 + 0,3 • 0,5) = 19,435 млн руб.
Таким образом, смешанная схема начисления процентов более выгодна для банка.
Возможны финансовые контракты, в которых начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не равна целому числу подпериодов. В этом случае также возможно использование двух схем наращения исходной суммы Р:
1) схема сложных процентов
2) смешанная схема
Обращаем внимание читателя на то, что в приведенных алгоритмах показатели ω и ƒ имеют разный смысл. Так в формуле (6,12) ω означает целое число лет в n годах, а ƒ — дробную часть года и поэтому n = ω + ƒ, Однако в формуле (6.14) ω означает целое число подпериодов в n годах, а ƒ — дробную часть подпериода и поэтому 
. Иными словами, при пользовании этими формулами надо отдавать себе отчет в том, о каком базисном периоде идет речь.
Источник
Смешанный способ начисления процентов формула
При дробном числе лет проценты начисляются разными способами:
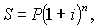
2) На основе смешанного метода, согласно которому за целое число лет начисляются сложные проценты, а за дробное — простые
(1)
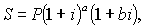
где п = а + b , a — целое число лет, b — дробная часть года.
3) В ряде коммерческих банков применяется правило, в соответствии с которым за отрезки времени меньше периода начисления проценты не начисляются, т.е.
(2)
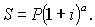
Поскольку b 1 , где b – дробная часть, то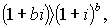 
следовательно, наращенная сумма, вычисленная по формуле (1), будет больше суммы, вычисленной по формуле сложных процентов. Можно показать, что при малых i наибольшая величина разности при расчетах по этим формулам достигается при b = 0,5.
Банк предоставил ссуду в размере 100 тыс.р. на 30 месяцев под 30% сложных годовых на условиях ежегодного начисления процентов. Какую сумму предстоит заемщику вернуть банку по истечению срока ссуды? Расчет произвести по 3-м способам. Провести анализ полученных результатов расчета.
Определим суммы, которые необходимо вернуть банку по 3-м способам.
S 1 = 100 (1 + 0,3) 2,5 = 192,69 тыс . р .,
S 2 = 100 (1 + 0,3) 2 (1 + 0,3 × 0,5) = 194, 35 тыс . р .,
S 3 = 100 (1 + 0,3) 2 = 169 тыс. р.
По 1-му способу заемщику предстоит вернуть банку 192,69 т.р., по 2-му способу на основе смешанного метода – 194,35 т.р., по 3-му способу –169 т.р.
Вариант расчета по 3-му способу выгоден заемщику, вариант расчета по 2-му способу выгоден банку.
Источник
Начисление процентов по смешанной схеме.
Начисление процентов по смешанной схеме представляет собой метод начисления процентов при котором используется схема сложных процентов для целого числа лет и схема простых процентов — для дробной части года.
Применяется данный метод в случае заключения кредитных договоров на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться по схеме сложных процентов или по смешанной схеме.
Расчет проводится по следующей формуле:
Fn = P * (1+r) w * (1+f*r)
где w — целое число лет; f — дробная часть года; п = w + f.
Начисление непрерывных процентов.
Начисление непрерывных процентов представляет совой метод начисления процентов при котором проценты начисляются за очень малые промежутки времени.
Такой метод особенно актуален, когда финансовые операции осуществляются и регистрируются с помощью электронных методов и осуществляется непрерывная капитализация.
В этом случае наращенная сумма находится по формуле:
Fn = Р * е r п
где r — непрерывная ставка (ее также называют силой роста).
e – число Эйлера ( равно 2,78)
Процентный доход составит величину:
I=Р * [е r n -1]
Формула непрерывной капитализации позволяет вычислить капитал в любом периоде времени.
Задачи
Клиент поместил в банк вклад в сумме 30 тыс. руб. под 14% годовых с ежемесячной выплатой процентов. Какой процентный доход он будет получать каждый месяц?
Зная, что Р = 30 тыс. руб., n =1/12года r = 0,14, получаем
Источник
Смешанный способ начисления процентов формула
4.1 Вычисление наращенной суммы на основе сложных декурсивных процентов
1. Формула наращения. В средне- и долгосрочных финансово- кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, приме няют сложные проценты. База для начисления сложных процентов в отличие от простых не остается постоян ной – она увеличивается с каждым шагом во времени. Абсолютная сумма начисляемых процентов возрастает, и процесс увеличения суммы долга происходит с ускорением. Наращение по сложным процентам можно представить как последователь ное реинвестирование средств, вложенных под простые про центы на один период начисления ( running period ). Присоедине ние начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов.
Найдем формулу для расчета наращенной суммы при усло вии, что проценты начисляются и капитализируются один раз в году (годовые проценты). Для этого применяется сложная став ка наращения. Для записи формулы наращения применим те же обозначения, что и в формуле наращения по простым про центам:
P — первоначальный размер долга (ссуды, кредита, капита ла и т.д.),
S — наращенная сумма на конец срока ссуды,
п — срок, число лет наращения,
i — уровень годовой ставки процентов, представленный де сятичной дробью.
Очевидно, что в конце первого года проценты равны величине Р i , а наращенная сумма составит 
. К конц у второго года она достигнет величины 
В конце n -го года наращенная сумма будет равна
(4.1)
Проценты за этот же срок в целом таковы:
(4.2)
Часть из них поучена за счет начисления процентов на проценты. Она составляет
(4.3)
Как показано выше, рост по сложным процентам представ ляет собой процесс, соответствующий геометрической прогрес сии, первый член которой равен Р , а знаменатель – 
. Последний член прогрессии равен наращенной сумме в конце срока ссуды.
Величину 
называют множителем наращения по сложным процентам. Значения этого множителя для целых чисел п приводятся в таблицах сложных процентов. Точность расчета множителя в практических расчетах определяется допустимой степенью округления наращенной суммы (до последней копейки, рубля и т.д.).
Время при наращении по сложной ставке обычно измеряет ся как АСТ/ A СТ.
Как видим, величина множителя наращения зависит от двух параметров — i и п. Следует отметить, что при большом сроке наращения даже небольшое изменение ставки заметно влияет на величину множителя. В свою очередь очень большой срок приводит к устрашающим результатам даже при небольшой процентной ставке.
Формула наращения по сложным процентам получена для годовой процентной ставки и срока, измеряемого в годах. Однако ее можно применять и при других периодах начисле ния. В этих случаях i означает ставку за один период начисления (месяц, квартал и т.д.), а n – число таких периодов. На пример, если i – ставка за полугодие, то п – число полугодий и т.д.
Формулы (4.1) — (4.3) предполагают, что проценты на про центы начисляются по той же ставке, что и при начислении на основную сумму долга. Усложним условия начислений процен тов. Пусть проценты на основной долг начисляются по ставке i а проценты на проценты – по ставке 
В этом случае
Ряд в квадратных скобках представляет собой геометриче скую прогрессию с первым членом, равным 1, и знаменателем 
. В итоге имеем
(4.4)
· Пример 4.1
2. Начисление процентов в смежных календарных периодах. Вы ше при начислении процентов не принималось во внимание расположение срока начисления процентов относительно календарных периодов. Вместе с тем, часто даты начала и окончания ссуды находятся в двух периодах. Ясно, что начисленные за весь срок проценты не могут быть отнесены только к послед нему периоду. В бухгалтерском учете, при налогообложении, наконец, в анализе финансовой деятельности предприятия воз никает задача распределения начисленных процентов по пери одам.
Общий срок ссуды делится на два периода n 1 и n 2 . Соответственно ,
где 
· Пример 4.2
3. Переменные ставки. Формула предполагает постоянную ставку на протяжении всего срока начисления процентов. Неустойчивость кредитно-денежного рынка заставляет модернизировать “классическую” схему, например, с помощью приме нения плавающих ставок ( floating rate ). Естественно, что расчет на перспективу по таким ставкам весьма условен. Иное дело — расчет постфактум. В этом случае, а также тогда, когда измене ния размеров ставок фиксируются в контракте, общий множи тель наращения определяется как произведение частных, т.е.
(4.5)
где 
— последовательные значения ставок; 
— периоды, в течение которых “работают” соответствующие ставки.
· Пример 4.3
4. Начисление процентов при дробном числе лет. Часто срок в го дах для начисления процентов не является целым числом. В правилах ряда коммерческих банков для некоторых операций проценты начисляются только за целое число лет или других периодов начисления. Дробная часть периода отбрасывается. В большинстве же случаев учитывается полный срок. При этом применяют два метода. Согласно первому, назовем его общим, расчет ведется по формуле:
(4.6)
Второй, сме шанный, метод предполагает начисление процентов за целое число лет по формуле сложных процентов и за дробную часть срока по формуле простых процентов:
, (4.7)
где 
– срок ссуды, а — целое число лет, b — дробная часть года.
Аналогичный метод применяется и в случаях, когда перио дом начисления является полугодие, квартал или месяц.
При выборе метода расчета следует иметь в виду, что мно житель наращения по смешанному методу оказывается несколько больше, чем по общему, так как для п во соотношение 
Наибольшая разница наблю дается при b = 1/2.
· Пример 4.4
5. Сравнение роста по сложным и простым процентам. Пусть временная база для начисления одна и та же, уровень процентных ставок совпадает, тогда:
1) для срока меньше года простые проценты больше сложных
2) для срока больше года
3) для срока 1 год множители наращения равны друг другу
Используя коэффициент наращения по простым и сложным процентам можно определить время, необходимое для увеличения первоначальной суммы в n раз. Для этого необходимо, что бы коэффициенты наращения были равны величине n :
1) для простых процентов
2) для сложных процентов
Формулы для удвоения капитала имеют вид:
а) 
б) 
6. Номинальная и эффективная ставка процентов. Годовая ставка при начислении процентов несколько раз в год называется номинальной ставкой j , кроме того, указывается число периодов начисления процентов в год m , тогда сумма вычисляется по формуле:
(4.8)
· Пример 4.6
Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена или по общей формуле или по общему методу:
где ml –число полных периодов начисления;
а – дробная часть одного периода начисления.
· Пример 4.7
7. Эффективная ставка. Она измеряет тот реальный относительный доход, который получает кредито в целом за год, т.е. она показывает, какую годовую ставку сложных процентов необходимо установить, что бы получить такой же финансовый результат, как и при m разовом начислении процентов по ставке j / m . Эта ставка определяется из равенства:
если первоначальная сумма периода наращения и множитель наращения равны, тогда
(4.9)
Из этого равенства можно определить номинальную ставку:
(4.10)
· Пример 4.8
Эффективную ставку можно рассчитать, зная наращенную сумму и величину первоначального вклада:
(4.11)
Срок ссуды определяется по формулам:
(4.12)
Источник
