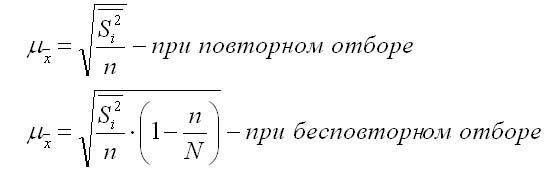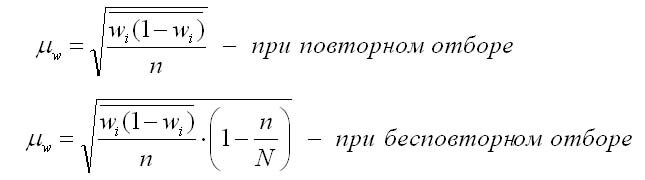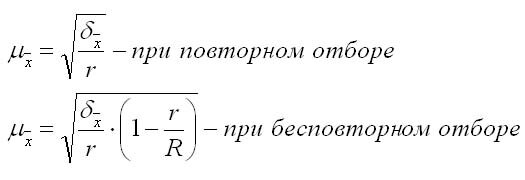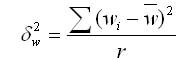- Виды выборки.
- ОСНОВНЫЕ СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ
- Механическая, типическая и серийная выборка
- Механическая выборка
- Типическая выборка
- Средняя ошибка типической выборки
- Серийная (гнездовая) выборка
- Расчет средней ошибки серийной (гнездовой) выборки
- Комбинированная выборка
- Выборочное наблюдение в статистике
- Понятие и виды выборочного наблюдения
- Ошибки выборки
Виды выборки.
Поможем написать любую работу на аналогичную тему
Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или невключение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Собственно-случайный отбор может быть как повторным, так и бесповторным. Для проведения бесповторного отбора в процессе жеребьевки выпавшие жребии обратно в исходную совокупность не возвращаются и в дальнейшем отборе не участвуют. При использовании таблиц случайных чисел бесповторность отбора достигается пропуском чисел в случае их повторения в выбранном столбце или столбцах.
Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.).
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или с его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно отбор начинать с середины первого интервала
Типический отбор. Этот способ отбора используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследовании населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасль или под-отрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внутригрупповой вариацией.
Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Источник
ОСНОВНЫЕ СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ
Поможем написать любую работу на аналогичную тему
Результаты выборочного наблюдения, размер ошибки выборки и методы ее определения зависят от способа и метода формирования выборочной совокупности.
Существует два МЕТОДА ОТБОРА единиц из генеральной совокупности в выборочную: бесповторный и повторный.
БЕСПОВТОРНЫМ называется такой отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.
При ПОВТОРНОМ ОТБОРЕ попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность.
МЕТОД ОТБОРА определяет возможность продолжения участия отобранной единицы в процедуре отбора.
СПОСОБ ОТБОРА – это конкретный механизм или процедура выборки единиц из генеральной совокупности.
Различают четыре вида (способа) формирования выборочной совокупности:
Ø случайный (собственно случайный);
Ø серийный (гнездовой).
СЛУЧАЙНЫЙ ОТБОР. При этом способе отбора единицы из генеральной
совокупности выбираются наугад, без каких- либо элементов системности.
Технически собственно случайный отбор производится методом жеребьевки или
по таблице случайных чисел.
Собственно – случайный отбор может быть как повторным, так и бесповторным.
МЕХАНИЧЕСКИЙ ОТБОР . Применяется в тех случаях, когда генеральная
совокупность, каким – либо образом упорядочена ( по алфавиту, по табельным
номерам, по адресам и т. п.). Для проведения такой выборки устанавливается
пропорция отбора, например, каждая десятая единица, каждая 50-я единица.
ТИПИЧЕСКАЯ ВЫБОРКА используется в тех случаях, когда единицы генеральной совокупности можно разбить на несколько типических групп. При обследовании населения такими группами могут быть социальные группы, возрастные или образовательные; при обследовании предприятий – группы по формам собственности, по отраслям и т. д.
Отбор единиц для исследования производится собственно случайным или механическим способом.
СЕРИЙНЫЙ ОТБОР. Отбору подлежат не отдельные единицы совокупности, а целые группы (гнезда, серии), отобранные собственно случайным или механическим способом.
Источник
Механическая, типическая и серийная выборка
Механическая выборка
Механическая выборка характеризуется тем, что отбор единиц в выборочную совокупность из генеральной, разбитую по нейтральному признаку на равные интервалы, в задачах статистики проводится так, что из каждой такой группы в выборку отбирается лишь одна единица.
Для того, чтобы избежать систематической ошибки, отбирается единица, которая находится в середине каждой группы.
При организации механического отбора единицы совокупности заранее располагают в определенном порядке и далее отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.
При анализе достаточно большой совокупности механический отбор по точности результатов близок к случайному. Поэтому для определения средней ошибки механической выборки пользуются формулами собственно-случайной бесповторной выборки.
Типическая выборка
Типическую выборку применяют для отбора единиц из неоднородной совокупности. Она используется тогда, когда все единицы генеральной совокупности можно разбить на несколько качественно однотипных групп по признакам, которые влияют на изучаемые показатели.
При анализе предприятий такими группами могут быть: отрасль, формы собственности, специфика работы и т. д. Затем из каждой типической группы механической или собственно-случайной выборкой производят индивидуальный отбор единиц в выборочную совокупность.
Часто типическая выборка применяется при анализе сложных статистических совокупностей (например, производительность труда рабочих организации, представленных отдельными группами по квалификации).
Такой вид выборки дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.
При расчете средней ошибки типической выборки в качестве показателя вариации берут среднюю из внутригрупповых дисперсий.
Средняя ошибка типической выборки
1. Для средней количественного признака:
где S — средняя из внутригрупповых дисперсий по выборочной совокупности.
2. Для доли (альтернативного признака):
где w(1 -w) – числитель — средняя из внутригрупповых дисперсий доли (альтернативного признака) по выборочной совокупности.
Серийная (гнездовая) выборка
В серийной выборке происходит случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп, с тем чтобы в этих группах все единицы были подвергнуты наблюдению.
Серийная выборка определена тем, что многие товары для их транспортировки, хранения или продажи упаковываются, следовательно при контроле качества упакованного товара рациональнее провести проверку несколько серий упаковок, чем из всех упаковок отбирать необходимое количество товара.
В связи с тем, что внутри групп (или серий) анализируются все единицы, средняя ошибка выборки при отборе равновеликих серий зависит только от межгрупповой (или межсерийной) дисперсии.
Расчет средней ошибки серийной (гнездовой) выборки
1. Для средней количественного признака:
где r — число отобранных серий;
R — общее число серий; дельта-квадрат — межгрупповая дисперсия серийной выборки, рассчитанная по формуле:
где xi — средняя i-й серии;
х — ошибка средняя по всей выборочной совокупности.
2. Для доли (альтернативного признака):
Межгрупповая (межсерийная) дисперсия доли серийной выборки определяется по формуле:
где w — доля признака в i-й серии;
w — общая доля признака во всей выборочной совокупности.
Комбинированная выборка
Комбинированную выборку применяют зачастую в практике выборочных наблюдений в разном сочетании их способов и видов.
Если в комбинированной выборке использовались механическая и типическая выборки, то средняя ошибка определяется по формуле:
где значения в формуле — средние ошибки механической и типической выборок.
Источник
Выборочное наблюдение в статистике
Понятие и виды выборочного наблюдения
Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.
Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив — генеральную совокупность (ГС). При этом число единиц в выборке обозначают n, а во всей ГС — N. Отношение n/N называется относительный размер или доля выборки.
Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.
Существует 4 способа случайного отбора в выборку:
- Собственно случайный отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел.
Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная.
При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.
Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.
Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.
Ошибки выборки
Выборочную совокупность можно сформировать по количественному признаку статистических величин, а также по альтернативному или атрибутивному. В первом случае обобщающей характеристикой выборки служит выборочная средняя величина, обозначаемая 
, а во втором — выборочная доля величин, обозначаемая w. В генеральной совокупности соответственно: генеральная средняя 
и генеральная доля р.
Разности 
— 
и W — р называются ошибкой выборки, которая делится на ошибку регистрации и ошибку репрезентативности. Первая часть ошибки выборки возникает из-за неправильных или неточных сведений по причинам непонимания существа вопроса, невнимательности регистратора при заполнении анкет, формуляров и т.п. Она достаточно легко обнаруживается и устраняется. Вторая часть ошибки возникает из-за постоянного или спонтанного несоблюдения принципа случайности отбора. Ее трудно обнаружить и устранить, она гораздо больше первой и потому ей уделяется основное внимание.
Величина ошибки выборки может быть разной для разных выборок из одной генеральной совокупности, поэтому в статистике определяется средняя ошибка повторной и бесповторной выборки по формулам:
— повторная;
— бесповторная;
где Дв — выборочная дисперсия.
Например, на заводе с численностью работников 1000 чел. проведена 5%-ая случайная бесповторная выборка с целью определения среднего стажа работников. Результаты выборочного наблюдения приведены в первых двух столбцах следующей таблицы:
X, лет
(стаж работы)f, чел.
(число работников в выборке)Xиf
Источник
