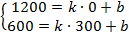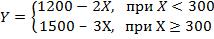2.3 Сложение некоторых КПВ
- Рассчитываем суммарные крайние точки (или одну крайнюю точку)
- Рассматриваем $AC$ какого-нибудь товара на всех участках всех КПВ
- Располагаем эти участки в соответствии с законом возрастающей $AC$
Пример 1
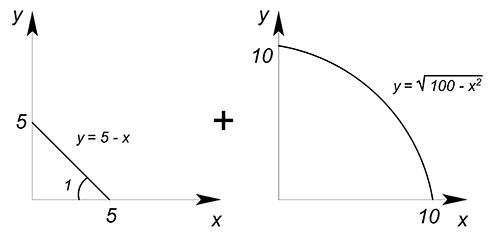
Найдите суммарную КПВ двух стран:
Данные КПВ являются линейными функциями.
Рассчитаем суммарные крайние точки данных КПВ: по $y$: $10+5=15$, по $x$: $5+10=15$.
Рассмотрим $AC_x$: первая функция обладает постоянной (ибо функция линейная) $AC_x=\dfrac<10><5>=2$; вторая функция обладает также постоянной $AC_x$, но уже равной $\dfrac<5><10>=\dfrac<1><2>$. Первый участок суммарной КПВ будет представлен функцией с меньшей $AC_x=\dfrac<1><2>$, а на втором участке $AC_x=2$.

Найдите суммарную КПВ двух стран:
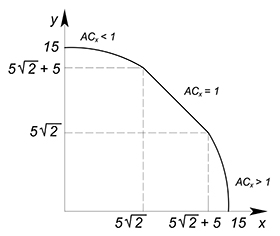
В данном случае мы имеем одну линейную и одну вогнутую КПВ.
Крайние точки суммарной КПВ: по $y$: $5+10=15$, по $x$: $5+10=15$.
Теперь перейдем к оценке альтернативной стоимости. У линейной функции она постоянна и по $x$ равна $\dfrac<5><5>=1$. $AC_x$ вогнутой функции не является константой. Она возрастает на при движении вдоль оси $x$ ($tg$ углов наклона касательных, проведенных к каждой точке данного графика возрастают). Для построения суммарной КПВ необходимо расположить участки в соответствии с законом возрастающей альтернативной стоимости. Поэтому нам надо найти на вогнутой КПВ участки, где $AC_x>1$ и где $AC_x 1$.
При совместном производстве благ тот или иной товар будет производить тот субъект, у которого это получается лучше всего (то есть с наименьшими альтернативными издержками). В такой ситуации ресурсы каждого производителя будут использоваться максимально эффективно, ибо они будут задействованы в создании того блага, для которого подходят лучше всего (например, если мы выращиваем морковь и ловим рыбу, то в данном случае лопатой будут копать, а не использовать её вместо весла). Поэтому, работая вместе, две страны смогут произвести больше благ, чем при индивидуальной работе.
Источник
Аналитическая запись
Решение
А) Построение КПВ
ШАГ 1
Изобразим линии производственных возможностей участков на графиках
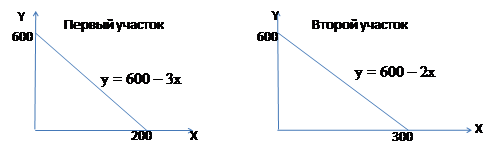 |
или запишем производственные возможности в виде таблицы
| Первый участок | Второй участок |
| Максимальный объем производства | |
| Сосен (Х) | |
| Елей (Y) |
ШАГ 2
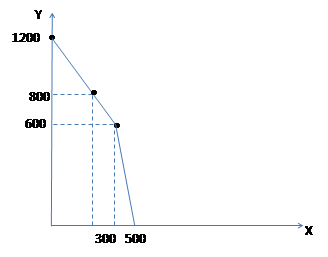
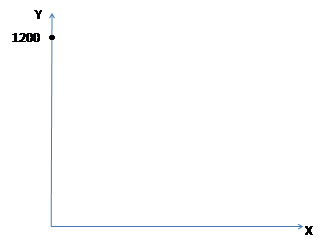
Нанесем максимальный объем производства елей (Y) на двух участках сразу (600+600=1200) на график общей КПВ.
 |
ШАГ 3
Итак, в отмеченной точке хозяйство лесника производит только ели. Начнем производить сосны. Но сначала следует определить, на каком участке лучше производить сосны в первую очередь, то есть какой участок обладает сравнительным преимуществом в производстве сосен. Это тот участок, где альтернативные издержки производства сосен наименьшие.
Определяем альтернативные издержки производства сосен на каждом участке:
| Первый участок | Второй участок | |
| Максимальный объем производства | ||
| Сосен (Х) | ||
| Елей (Y) | ||
| Альтернативные издержки производства сосен | ||
| Сосен (Х) | ||
| Елей (Y) | 1/3 | 1/2 |
Способ расчета альтернативных издержек. Для первого участка: если на нем будет произведено 600 елей, то не будет произведено 200 сосен и наоборот. То есть альтернативные издержки производства 600 елей составляет 200 сосен, а альтернативные издержки производства 200 сосен – 600 елей. Значит, альтернативные издержки производства 1 сосны равны 3 елям, а альтернативные издержки производства 1 ели – 1/3 сосны.
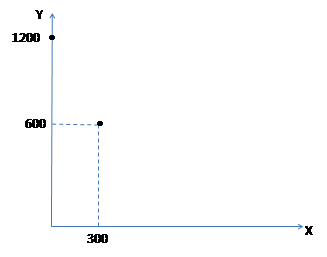
ШАГ 4

Аналитическая запись
Каждый участок описывается линейной функцией, параметры которой восстанавливаются по двум точкам.
Верхний участок проходит через точки с координатами (0;1200) и (300;600). Решаем систему уравнений
Из ее решения получаем параметры функции:
Аналогично получается уравнение второго участка КПВ: 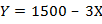
Таким образом, общая КПВ аналитически описывается следующим образом:
А можно сделать так, как мы разбирали на семинаре.
Б) Определить, сколько сосен сможет вырастить лесник, если фирма «Дед Мороз» заказала ему 800 елей, можно двумя способами.
1 способ – воспользоваться графиком и аналитическим описанием. Точка, соответствующая производству 800 елей лежит на верхнем участке общей КПВ, который описывается уравнением 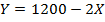
2 способ(если нет аналитического описания). Для производства елей в первую очередь нужно использовать первый участок, так как альтернативные издержки их производства там наименьшие. Таким образом, он весь будет засажен елями (600) и еще 200 нужно будет вырастить на втором участке. Альтернативные издержки производства одной ели на нем равны ½ сосны. Следовательно, если нужно вырастить 200 елей, то придется отказаться от 100 сосен. А так как максимальное производство сосен на втором участке равно 300, то останется 300-100=200 сосен.
Источник
2.3 Сложение некоторых КПВ
- Рассчитываем суммарные крайние точки (или одну крайнюю точку)
- Рассматриваем $AC$ какого-нибудь товара на всех участках всех КПВ
- Располагаем эти участки в соответствии с законом возрастающей $AC$
Пример 1
Найдите суммарную КПВ двух стран:
Данные КПВ являются линейными функциями.
Рассчитаем суммарные крайние точки данных КПВ: по $y$: $10+5=15$, по $x$: $5+10=15$.
Рассмотрим $AC_x$: первая функция обладает постоянной (ибо функция линейная) $AC_x=\dfrac<10><5>=2$; вторая функция обладает также постоянной $AC_x$, но уже равной $\dfrac<5><10>=\dfrac<1><2>$. Первый участок суммарной КПВ будет представлен функцией с меньшей $AC_x=\dfrac<1><2>$, а на втором участке $AC_x=2$.
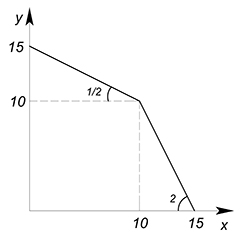
Найдите суммарную КПВ двух стран:
В данном случае мы имеем одну линейную и одну вогнутую КПВ.
Крайние точки суммарной КПВ: по $y$: $5+10=15$, по $x$: $5+10=15$.
Теперь перейдем к оценке альтернативной стоимости. У линейной функции она постоянна и по $x$ равна $\dfrac<5><5>=1$. $AC_x$ вогнутой функции не является константой. Она возрастает на при движении вдоль оси $x$ ($tg$ углов наклона касательных, проведенных к каждой точке данного графика возрастают). Для построения суммарной КПВ необходимо расположить участки в соответствии с законом возрастающей альтернативной стоимости. Поэтому нам надо найти на вогнутой КПВ участки, где $AC_x>1$ и где $AC_x 1$.
При совместном производстве благ тот или иной товар будет производить тот субъект, у которого это получается лучше всего (то есть с наименьшими альтернативными издержками). В такой ситуации ресурсы каждого производителя будут использоваться максимально эффективно, ибо они будут задействованы в создании того блага, для которого подходят лучше всего (например, если мы выращиваем морковь и ловим рыбу, то в данном случае лопатой будут копать, а не использовать её вместо весла). Поэтому, работая вместе, две страны смогут произвести больше благ, чем при индивидуальной работе.
Источник
5.2 Алгоритм построения общей КПВ
Даны 2 линейных КПВ с различными альтернативными издержками производства двух товаров: А и В
Посчитаем альтернативные издержки (АИ) для каждого блага на каждом поле (они пригодятся нам чуть позже):
| Поле 1 | Поле 2 |
|---|---|
Найдем максимальные координаты товаров А и В, которые можно суммарно произвести суммарно на обоих полях. Это легко сделать простым суммированием максимальных координат соответствующих товаров на отдельных полях. Суммарное максимальное количество товара А составляет 300 (200 + 100), товара B такое 3000 (100 + 200).
Далее мы начнем двигаться от точки с максимальным производство товара А, то есть точки с координатами (0;300). Мы будем последовательно увеличивать производство товара B от нуля до его максимума. В процессе увеличения производства товара В нам предстоит решить задачу, на каком поле производить товар В в первую очередь, на каком поле производить потом, и так далее, до тех пор, пока товар В не будет произведен на всех полях. Делая это, мы будем держать в голове простое правило: товар В мы произведем в первую очередь на том поле, где альтернативные издержки производства товара В наименьшие. Потом мы опять выберем поле, где альтернативные издержки товара В наименьшие из оставшихся полей, и так далее. Данный алгоритм работает для случая множества полей.
Случай с двумя полями является наиболее простым. Для случая двух полей от верхней точки мы вначале отложим поле с минимальными альтернативными издержками товара В, а затем оставшееся второе поле.
От максимальной координаты товара А (точки с координатами 0;300) мы построим второе поле, поскольку на нам альтернативные издержки товара В равны 0.5, что меньше, чем альтернативные издержки на первом поле, которые равны 2.
Для этого от точки с координатами (0;300) мы отложим 100 единиц А вниз и 200 единиц В вправо (это в точности координаты второго поля). Сделав это, мы попали в промежуточную точку с координатами (200;200).
Далее от получившейся промежуточной точки мы откладываем следующее поле с чуть более высокими альтернативными издержками товара В (в нашей случае это оставшееся поле).
Для этого из промежуточной точки мы отложим 200 единиц А вниз и 100 единиц В вправо (это в точности координаты оставшегося первого поля). После этого мы попадем в точку максимального производства товара В, то есть в точку с координатами (300;0).
Получившийся график и представляет собой объединенную КПВ. Этот график обладает интересной особенностью. Если просто покоординатно сложить точки, лежащие на отдельных КПВ то мы получим место точек, ограниченных жирной линией на графике ниже.
Однако график общей КПВ лежит выше данной линии. То есть при объединении полей общая экономика получает область, которая была недоступна ранее, когда поля рассматривались как независимые. Данный эффект имеет место в силу разной эффективности производства благ на разных полях. Как было показано в главе «Альтернативная стоимость», рациональные индивиды, делая выбор, минимизируют альтернативные затраты. Экономика, имея два поля, будет иметь возможность для специализации. В этих условиях экономика будет стараться производить товар на том поле, на котором имеет более низкие альтернативные издержки его производства (на экономическом языке имеет сравнительное преимущество). Промежуточная точка на графике называется точкой полной специализации, когда экономика производит один товар полностью на одном поле, а другой товар на втором поле.
Мы подошли к следующему важному разделу модели КПВ – специализация и обмен.
Идея специализации проста – каждая экономика старается производить тот товар, в котором имеет сравнительное преимущество, то есть меньшие альтернативные издержки. Данная идея легла в основу первой теории международной торговли, развитой англичанином Давидом Рикардо.
Концепция сравнительного преимущества резко контрастирует с идеей абсолютного преимущества. Абсолютное преимущество – способность производить больше товара с теми же затратами ресурсов, или же (определение наоборот) способность производить то же количество товара с меньшими затратами ресурсов. Иначе говоря, абсолютное преимущество это более высокая производительность.
Источник