Словесно формульный способ алгоритма решения задачи
Для составления программы, предназначенной для решения на ЭВМ какой-либо задачи, требуется составление алгоритма ее решения — точного предписания, которое определяет процесс, ведущий от исходных данных к требуемому конечному результату.
Алгоритм — предписание, однозначно задающее процесс преобразования исходной и нформации в виде последовательности элементарных дискретных шагов, приводящих за конечное число их применений к результату.
Алгоритмами, например, являются правила сложения, умножения, решения алгебраических уравнений, умножения матриц и т.п. Слово алгоритм происходит от algoritmi , являющегося латинской транслитерацией арабского имени хорезмийского математика IX века аль-Хорезми. Благодаря латинскому переводу трактата аль-Хорезми европейцы в XII веке познакомились с позиционной системой счисления, и в средневековой Европе алгоритмом называлась десятичная позиционная система счисления и правила счета в ней.
Алгоритм — это точная инструкция, а инструкции встречаются практически во всех областях человеческой деятельности. Возможны алгоритмы проведения физического эксперимента, сборки шкафа или телевизора, обработки детали. Однако не всякая инструкция есть алгоритм.
Инструкция становится алгоритмом только тогда, когда она удовлетворяет определенным требованиям. Эти требования частично сформулированы в определении, хотя упомянутые в определении понятия однозначности и элементарности сами нуждаются в уточнении.
Алгоритм однозначен, если при применении к одним и тем же данным он даст один и тот же результат. Но как по описанию алгоритма определить, однозначен он или нет. В каком случае шаги считаются элементарными. …
Применительно к ЭВМ алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности возможных исходных данных и направленный на получение определенных этими исходными данными результатов. Термин вычислительный процесс распространяется и на обработку других видов информации, например, символьной, графической или звуковой.
| Свойства алгоритма. |
Если вычислительный процесс заканчивается получением результатов, то говорят, что соответствующий алгоритм применим к рассматриваемой совокупности исходных данных. В противном случае говорят, что алгоритм неприменим к совокупности исходных данных. Любой применимый алгоритм обладает следующими основными свойствами:
Дискретность – последовательное выполнение простых или ранее определённых (подпрограммы) шагов. Преобразование исходных данных в результат осуществляется дискретно во времени.
Определенность состоит в совпадении получаемых результатов независимо от пользователя и применяемых технических средств (однозначность толкования инструкций).
Результативность означает возможность получения результата после выполнения конечного количества операций.
Массовость заключается в возможности применения алгоритма к целому классу однотипных задач, различающихся конкретными значениями исходных данных (разработка в общем виде).
Для задания алгоритма необходимо описать следующие его элементы:
Д набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов;
Д правило начала;
Д правило непосредственной переработки информации (описание последовательности действий);
Д правило окончания;
Д правило извлечения результатов.
Алгоритм всегда рассчитан на конкретного исполнителя. В нашем случае таким исполнителем является ЭВМ. Для обеспечения возможности реализации на ЭВМ алгоритм должен быть описан на языке, понятном компьютеру, то есть на языке программирования.
Понятия алгоритма и программы разграничены не очень чётко. Обычно программой называют окончательный вариант алгоритма решения задачи, ориентированный на конкретного пользователя.
Таким образом, можно дать следующее определение программы для ЭВМ:
Программа — это описание алгоритма и данных на некотором языке программирования, предназначенное для последующего автоматического выполнения.
| Способы описания алгоритмов |
К основным способам описания алгоритмов можно отнести следующие:
Д словесно-формульный (на естественном языке);
Д структурный или блок-схемный;
Д с использованием специальных алгоритмических языков;
Д с помощью граф-схем (граф — совокупность точек и линий, в которой каждая линия соединяет две точки. Точки называются вершинами, линии — рёбрами);
Д с помощью сетей Петри.
Перед составлением программ чаще всего используются словесно-формульный и блок-схемный способы. Иногда перед составлением программ на низкоуровневых языках программирования типа языка Ассемблера алгоритм программы записывают, пользуясь конструкциями некоторого высокоуровнего языка программирования. Удобно использовать программное описание алгоритмов функционирования сложных программных систем. Так, для описания принципов функционирования ОС использовался Алголо-подобный высокоуровневый язык программирования.
Словесно-формульный способ.
Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:
1. Ввести значения а и х.
2. Сложить х и 6.
3. Умножить а на 2.
4. Вычесть из 2а сумму (х+6).
5. Вывести у как результат вычисления выражения.
Блок-схемы.
Блок-схема должна содержать все разветвления, циклы и обращения к подпрограммам, содержащиеся в программе.
Условные обозначения блоков схем алгоритмов.
Источник
Словесно-формульный способ.
Присловесно-формульном способе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий.
Пусть, например, необходимо найти значение следующего выражения:
Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:
1. Ввести значения а и х.
2. Сложить х и 6.
3. Умножить а на 2.
4. Вычесть из 2а сумму (х+6).
5. Вывести у как результат вычисления выражения.
Блок-схемы.
Приблок-схемном описании алгоритм изображается геометрическими фигурами (блоками), связанными по управлению линиями (направлениями потока) со стрелками. В блоках записывается последовательность действий.
Данный способ по сравнению с другими способами записи алгоритма имеет ряд преимуществ. Он наиболее нагляден: каждая операция вычислительного процесса изображается отдельной геометрической фигурой. Кроме того, графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали.
Оформление программ должно соответствовать определенным требованиям. В настоящее время действует единая система программной документации (ЕСПД), которая устанавливает правила разработки, оформления программ и программной документации. В ЕСПД определены и правила оформления блок-схем алгоритмов (ГОСТ 10.002-80 ЕСПД, ГОСТ 10.003-80 ЕСПД).
Операции обработки данных и носители информации изображаются на схеме соответствующимиблоками. Большая часть блоков по построению условно вписана в прямоугольник со сторонами а и b. Минимальное значение а равно 10 мм, увеличение а производится на число, кратное 5 мм. Размер b=1,5 мм. Для отдельных блоков допускается соотношение между а и b, равное 1:2. В пределах одной схемы рекомендуется изображать блоки одинаковых размеров. Все блоки нумеруются. Виды и назначение основных блоков приведены в табллице.
Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки. Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз. В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков. Из блока (кроме логического) может выходить только одна линия. Логический блок может иметь в качестве продолжения одни из двух блоков, и из него выходят две линии. Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить.
Схему алгоритма следует выполнять как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки.
Если при обрыве линии продолжение схемы находится на этом же листе, то на одном и другом конце линии изображается специальный символсоединитель — окружность диаметром 0,5 мм. Внутри парных окружностей указывается один и тот же идентификатор. В качестве идентификатора, как правило, используется порядковый номер блока, к которому направлена соединительная линия. Если схема занимает более одного листа, то в случае разрыва линии вместо окружности используется межстраничный соединитель. Внутри каждого соединителя указывается адрес — откуда и куда направлена соединительная линия. Адрес записывается в две строки: в первой указывается номер листа, во второй — порядковый номер блока.
Блок-схема должна содержать все разветвления, циклы и обращения к подпрограммам, содержащиеся в программе.
Таблица. Условные обозначения блоков схем алгоритмов.
| Наименование | 0бозначенне | Функции |
| Процесс | Выполнение операции или группы операции, в результате которых изменяется значение, форма представления или расположение данных. | |
| Ввод-вывод | Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод). | |
| Решение | Выбор направления выполнения алгоритма в зависимости от некоторых переменных условии. | |
| Предопределенный процесс | Использование ранее созданных и отдельно написанных программ (подпрограмм). | |
| Документ | Вывод данных на бумажный носитель. | |
| Магнитный диск | Ввод-вывод данных, носителем которых служит магнитный диск. | |
| Пуск-останов | Начало, конец, прерывание процесса обработки данных. | |
| Соединитель | Указание связи между прер ванными линиями, соединяющими блоки. | |
| Межстраничный соединитель | Указание связи между прерванными линиями, соединяющими блоки, расположенные на разных листах. | |
| Комментарий | Связь между элементом схемы и пояснением. |
20)Структурные схемы алгоритмов.
Одним из свойств алгоритма является дискретность — возможность расчленения процесса вычислений, предписанных алгоритмом, на отдельные этапы, возможность выделения участков программы с определенной структурой. Можно выделить пять простейших структур:
@ Следование (последовательность двух или более операций);
@ Ветвление (выбор направления);
@ Повторение (цикл «до» и цикл «пока»).
Заметим при этом, что две последние структуры можно реализовать, используя структуру типа ветвление. Таким образом, любой вычислительный процесс может быть представлен как комбинация трёх элементарных алгоритмических структур. Соответственно, вычислительные процессы, выполняемые на ЭВМ по заданной программе, можно разделить на три основных вида:
Линейные процессы.
Линейным принято называть вычислительный процесс, в котором операции выполняются последовательно, в порядке их записи. Каждая операция является самостоятельной, независимой от каких-либо условий. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности.
Линейные вычислительные процессы имеют место, например, при вычислении арифметических выражений, когда имеются конкретные числовые данные и над ними выполняются соответствующие условию задачи действия. На рисунке показан пример линейного алгоритма, определяющего процесс вычисления арифметического выражения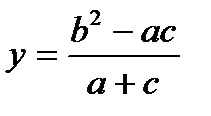 
.
Ветвящиеся процессы.
Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе — это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей — сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» — условие выполнено и «нет» — условие не выполнено.
Следует иметь в виду,что, хотяна схеме алгоритма должны быть показанывсевозможные направления вычислений в зависимости от выполнения определенного условия (или условии), при однократном прохождении программы процесс реализуется только по одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса. На рисунке показан пример алгоритма с разветвлением для вычисления следующего выражения:
Циклические процессы.
Циклическими называются программы, содержащие циклы. Цикл — это многократно повторяемый участок программы.
В организации цикла можно выделить следующиеэтапы:
@ 
подготовка (инициализация) цикла (И);
@ выполнение вычислений цикла (тело цикла) (Т);
@ модификация параметров (М);
@ проверка условия окончания цикла (У).
Порядок выполнения этих этапов, например, Т и М, может изменяться. В зависимости от расположения проверки условия окончания цикла различают циклы с нижним и верхним окончаниями. Для цикла с нижним окончанием тело цикла выполняется как минимум один раз, так как сначала производятся вычисления, а затем проверяется условие выхода из цикла.
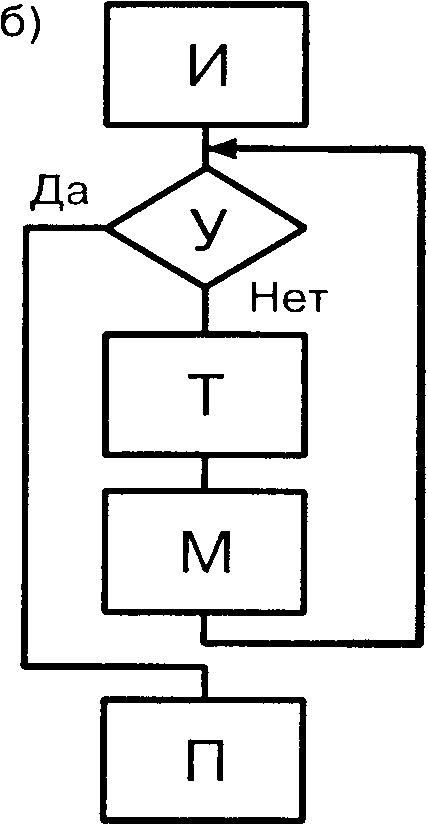
В случае цикла с верхним окончанием тело цикла можетне выполниться ни разу в случае, если сразу соблюдается условие выхода.
Цикл называетсядетерминированным, если число повторений тела цикла заранее известно или определено. Цикл называетсяитерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях.
Решение задач на ЭВМ.
21)Этапы подготовки и решения задач на ЭВМ.
На ЭВМ могут решаться задачи различного характера, например: научно-инженерные; разработки системного программного обеспечения; обучения; управления производственными процессами и т. д. В процессе подготовки и решенияна ЭВМ научно-инженерных задач можно выделить следующиеэтапы:
1. постановка задачи;
2. математическое описание задачи;
3. выбор и обоснование метода решения;
4. алгоритмизация вычислительного процесса;
5. составление программы;
6. отладка программы;
7. решение задачи на ЭВМ и анализ результатов.
В задачах другого класса некоторые этапы могут отсутствовать, например, в задачах разработки системного программного обеспечения отсутствует математическое описание.
Перечисленные этапы связаны друг с другом. Например, анализ результатов может показать необходимость внесения изменений в программу, алгоритм или даже в постановку задачи. Для уменьшения числа подобных изменений необходимо на каждом этапе по возможности учитывать требования, предъявляемые последующими этапами. В некоторых случаях связь между различными этапами, например, между постановкой задачи и выбором метода решения, между составлением алгоритма и программированием, может быть настолько тесной, что разделение их становится затруднительным.
Постановка задачи.
На данном этапе формулируется цель решения задачи и подробно описывается ее содержание. Анализируются характер и сущность всех величин, используемых в задаче, и определяются условия, при которых она решается. Корректность постановки задачи является важным моментом, так как от нее в значительной степени зависят другие этапы.
Источник
