Скорость точки векторный способ задания движения точки

Векторный способ задания движения точки

Введение

Положение точки однозначно определяется заданием ее радиус-вектора , который изменяется со временем при движении точки. При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.

Например, для точки, движущейся с постоянным ускорением , радиус-вектор определяется одной векторной формулой:
,
где – постоянные векторы, не зависящие от времени. Применяя формулы, мы можем найти кинематические величины в векторном виде, не зависимо от выбранной системы координат.

При координатном способе задания движения, мы выбираем систему координат, и в ней задаем зависимости координат точки от времени . Таким образом, координатный способ привязан к выбранной системе координат, а векторный способ не зависит от системы координат.

Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.

Основные формулы при векторном способе задания движения

Скорость точки

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.

Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.

Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.

Скорость точки направлена по касательной к траектории. Пусть – единичный вектор в направлении касательной. Тогда скорость может быть направленной либо вдоль вектора :
,
либо в противоположную сторону:
.
Чтобы охватить эти два случая, вводят алгебраическую величину скорости :
.
Это скалярная величина, равная по абсолютной величине модулю скорости, но она может принимать как положительные, так и отрицательные значения:
.
При , вектор скорости сонаправлен с . При он направлен в противоположную сторону. Величина является проекцией вектора скорости на направление . Поскольку – это единичный вектор, то
.

Единичный вектор в направлении касательной к траектории:
.

Ускорение точки

Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.

Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.

Тангенциальное ускорение

Алгебраическая величина тангенциального ускорения – это скалярная величина, равная проекции полного ускорения на направление единичного вектора , касательного к траектории:
.
Тогда вектор тангенциального ускорения можно записать в следующем виде:
.
Величина может быть как положительной, так и отрицательной. При положительном , вектор касательного ускорения сонаправлен с единичным вектором . При отрицательном – вектор касательного ускорения направлен в противоположную сторону. Модуль равен модулю касательного ускорения:
.
Алгебраическая величина тангенциального ускорения равна производной по времени от алгебраической величины скорости:
.
Производная по времени модуля скорости:
.
Если между векторами скорости и ускорения острый угол, то движение ускоренное. Если между ними тупой угол, то движение замедленное.

Нормальное ускорение

Вектор нормального ускорения:
.
; .
Единичный вектор в направлении главной нормали траектории:
.
Вектор перпендикулярен вектору и направлен к центру кривизны траектории. Нормальное ускорение всегда направлено к центу кривизны траектории. Поэтому, если выразить его через единичный вектор главной нормали:
,
то . Поэтому .
Модуль нормального ускорения равен проекции полного ускорения на направление главной нормали:
.
Имеют место следующие формулы:
.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Автор: Олег Одинцов . Опубликовано: 06-03-2016 Изменено: 29-01-2020

Источник

Векторный способ задания движения точки

Рассмотрим движение материальной точкиМ относительно некоторого тела, которое считается неподвижным. Пусть точка О – точка принадлежащая этому телу (рис.5.3). Радиус-вектор движущейся точки М относительно точкиО можно задать как вектор-функцию времени t

. (5.6)

Равенство (5.6) называется векторным уравнением движения точки или законом движения точки в векторной форме.

Кривая по которой движется точка в пространстве называется траекторией точки. Траектория – это годограф радиус-вектора точки.

Координатный способ задания движения точки

Пусть теперь вектор задан в декартовой системе координат, а— орты осейОх, Оу, Оz. Тогда вектор-функция может быть задана тремя скалярными функциями:

=++.

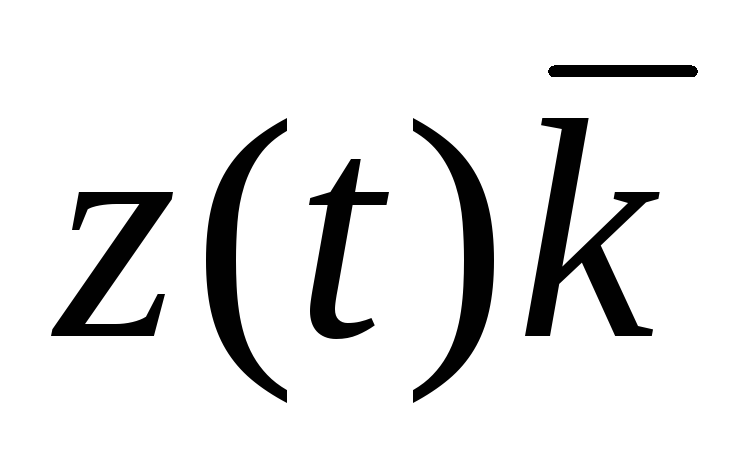
Таким образом, для того, чтобы движение точки было задано координатным способом, должны быть заданы функции:

Равенства (5.7) называются уравнениями движения точки или законом движения точки в координатной форме.

Естественный способ задания движения точки

Этот способ применяется в случае, когда траектория точки известна заранее. Траектория точки может быть задана различными способами: словесно (например, можно сказать, что траекторией точки является окружность такого-то радиуса), графически в каком-либо масштабе или уравнениями, например, в общем виде как линия пересечения поверхностей

,

или другими уравнениями.

Для задания закона движения точки по траектории необходимо выбрать на траектории точку М₀, принимаемую за начало отсчета дуговой координаты и задать положительное направление отсчета (рис. 5.4.).

При движении точки М расстояние от нее до начальной точки изменяется с течением времени, следовательно, дуговую координату необходимо задать как функцию времени:

Зависимость (5.8) называется законом движения точки. Следовательно, для того, чтобы движение точки было задано естественным способом, должны быть заданы:

положительное направление отсчета дуги s.

При этом нужно отличать дугу s и пройденный точкой путь. Если точка движется по траектории все время в одном направлении, то дуга и путь совпадают, но если, например закон движения точки равен и точка совершает гармонические колебания по кривой, то дуга и путь совпадают только до достижения дуги своего максимального значенияа. Далее путь в отличие от дуги будет все время увеличиваться.

Скорость и ускорение точки Скорость точки

Пусть движение точки задано векторным способом . На рис.5.9М и М₁  положения движущейся точки в моменты времени t и t + t.

Вектор называется вектором перемещения точки за времяt. Отношение вектора к промежут ку времени t называется средней скоростью точки за промежуток времени t

.

Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени за который произошло это перемещение, при стремлении последнего к нулю, т.е.

. (5.9)

Таким образом,скорость точки в данный момент времени равна производной радиусавектора точки по времени

. (5.10)

Это векторная величина, характеризующая быстроту изменения радиусавектора точки и направленная по касательной к траектории в сторону движения точки. Единицей измерения скорости в системе СИ является м/с.

Источник

19 Определение скорости точки при задании ее движения: координатным, векторным и естественным способами.

Векторный способ: вектор скорости точки в данный момент времени равен первой производной от радиуса вектора.

Координатный способ: проекции скорости точки на оси координат равна первым производным от соответствующих координат точки по времени.

Естественный способ: численная величина скорости в данный момент времени равна первой производной от расстояния S(t).

20 Определение ускорения точки при задании ее движения: координатным, векторным и естественным способами.

Векторный способ: вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус вектора точки по времени.

Координатный способ: проекция ускорения точки на какую-либо координатную ось равна первой производной от проекции ее на эту ось или второй производной от соответствующей координаты точки по времени.

Естественный способ: проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны в данной точке кривой.

21 Классификация движений.

а) равномерное аn=0 ат=0 а=0

б) неравномерное аn=0 ат=/0 a= ат=dv/dt=d^2S/dt^2

в) равнопеременное аn=0 ат=const

а) равномерное аn=/0 aт=0 a=an=v^2/p

изменяется вектор ускорения и направление по нормали к траектории(к центру)

б) неравномерное аn=/0 ат=/0

в) равнопеременное ат=const V=V0+- атt S=S0+V0t+- (атt^2)/2

22 Поступательное движение

Такое движение твердого тела, при котором любая прямая проведенная в этом теле перемещается, оставаясь параллельной самой себе.

При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю скорости и ускорения.

23 Вращательное движение.

Такое движение твердого тела, при котором все его точки лежащие на некоторой прямой, называемой осью вращения, остаются неподвижными.

1 угол поворота – между двумя полуплоскостями проведенными через ось вращения.

Угол «+» если откладывается против хода часовой стрелки от неподвижной плоскости.

2 Угловая скорость тела числено равна первой производной от угла поворота по времени.

3 Угловое ускорение

4 Быстрота движения , n

24 Скорости и ускорения точек вращающегося тела.

25 Частные случаи вращательного движения твердого тела.

26 Плоскопараллельное движение. Уравнения плоскопараллельного движения.

Такое движение тела, при котором все его точки перемещаются в плоскостях параллельных некоторой неподвижной плоскости.

27 Определение скоростей и ускорений при плоскопараллельном движении.

28 Мгновенный центр скоростей. Определение мгновенного центра скоростей.

Мгновенный центр скоростей — такая , неизменно связанная с плоской фигурой точка, скорость которой в данный момент времени равна нулю.

Мгновенный центр скоростей находится на пересечении перпендикуляров восстановленных из данной точки к линиям действия их скоростей.

Скорость любой точки тела, лежащей в сечении площади, равна ее вращательной скорости вокруг мгновенного центра скоростей.

29 Частные случаи определения мгновенного центра скоростей.

1 Тело катится без скольжения по некоторой неподвижной плоскости. Мгновенный центр находится в точке соприкосновения линий.

2 скорости А и В параллельны, но не перпендикулярны к линии АВ. VA=VB

Такое состояние движения тела называется мгновенно поступательным.

30 Сложное движение точки.

Такое движение точки, при котором точка (тело) участвует в двух или нескольких движениях.

Теорема о сложении скоростей.

При сложном движении абсол. Скорость равна геометрической сумме относительной и переносной скорости.

Теорема о сложении ускорений.

Равно удвоенному векторному произведению переносной угловой скорости на относительную скорость точки.

Случаи, когда ускорение Кориолиса равно нулю.

1vотн=0, точка не движется, а находится на поверхности.

2wпер=0, когда перенос движения не является вращательным.

3vотн // wпер, sin=0

31 Динамика – раздел теоретической механики, в котором изучается движение материальных тел под действием сил.

Основные законы динамики:

Изолированная от внешних воздействий материальная точка сохраняет состояние покоя или равновесия.

2)Основной закон динамики: F=ma

Ускорение, сообщаемое материальной точки, приложенной к ней силе пропорционально модулю этой силы и совпадает с ней по направлению.

3)Закон равенства действия и противодействия.

Две материальные точки действуют друг на друга силами, равными по модулю и направлению вдоль прямой, соединяющей эти точки в противоположную сторону.

32 Дифференциальные уравнения движения точки: естественный способ и координатный способ задания движения.

33 Первая задача динамики.

Зная m точки и уравнение ее движения найти модуль и направление равнодействующих сил, приложенных к точке.

34 Вторая (основная) задача динамики. (решается интегрированием)

Зная силы, действующие на точки, ее m, начальную скорость, начальное положение, определить уравнение ее движения.

35 Колебательное движение материальной точки.

1)Свободные колебания совершаются под действием восстанавливающейся силы.

2)Затухающие под действием двух сил восстанавливающейся и силы сопротивления.

а под действием восстанавливающей, возмущающей и силы сопротивления.

б под действием восстанавливающей и возмущающей сил.

Свободные гармонические колебания.

Происходят при условии, если на точку отклоненную от равновесия действует восстанавливающая сила, которая стремится вернуть ее положение равновесия.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник