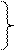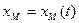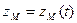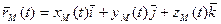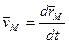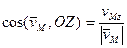Скорость точки при векторном и координатном способе задания движения.
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
1. Векторный и координатный (декартовы координаты), способы задания движения материальной точки. Скорость и ускорение точки для векторного и координатного (декартовы координаты) способов задания движения точки.
2. Естественный способ задания движения материальной точки. Скорость и ускорение точки для естественного способа задания движения.
3. Матрица взаимной ориентации двух трехгранников (матрица направляющих косинусов). Свойства строк и столбцов матрицы ориентации.
4. Стандартные матрицы ориентации.
5. Параметры ориентации твердого тела: углы Эйлера. Матрица направляющих косинусов как функция углов Эйлера.
6. Понятие угловой скорости одного трехгранника относительно другого.
7. Угловая скорость абсолютно твердого тела. Теорема о независимости угловой скорости от выбора полюса.
8. Связь между скоростями двух точек твердого тела. Теорема о проекциях скоростей двух точек твердого тела на прямую, их соединяющую.
9. Связь между ускорениями двух точек твердого тела (вращательное и осестремительное ускорения). Угловое ускорение твердого тела.
10. Поступательное движение твердого тела. Скорости и ускорения точек при поступательном движении твердого тела.
11. Вращение абсолютно твердого тела вокруг неподвижной оси. Уравнение вращательного движения. Скорости и ускорения точек твердого тела.
12. Плоско-параллельное движение абсолютно твердого тела. Уравнения плоскопараллельного движения. Скорости и ускорения точек твердого тела, направление угловой скорости и углового ускорения.
13. Понятие мгновенного центра скоростей (МЦС) при плоском движении твердого тела. Теорема о существовании и единственности МЦС. Способы нахождения МЦС.
14. Сложное движение точки: понятия абсолютной, относительной и переносной скоростей. Связь между производными вектора относительно разных трехгранников (формула Бура). Теорема о сложении скоростей.
15. Сложное движение точки: понятия абсолютного, относительного, переносного и кориолисова (добавочного) ускорений. Теорема о сложении ускорений (теорема Кориолиса).
16. Три закона Ньютона. Прямая и обратная задачи динамики.
17. Момент силы относительно точки. Проекции момента силы относительно точки на оси координат. Момент силы относительно оси.
18. Главный момент системы сил относительно точки. Главный вектор системы сил. Изменение главного момента при переносе точки приведения.
19. Пара сил. Независимость главного момента пары сил от центра приведения. Момент пары сил.
20. Внешние и внутренние силы системы материальных точек. Свойства системы внутренних сил.
21. Количество движения (импульс) системы материальных точек. Теорема об изменении импульса.
22. Центр масс системы материальных точек. Связь импульса системы материальных точек со скоростью центра масс. Теорема о движении центра масс.
23. Момент количества движения (кинетический момент) системы материальных точек относительно произвольного центра приведения. Теорема об изменении кинетического момента системы материальных точек относительно произвольного центра приведения. Случай неподвижного центра приведения и случай, когда центр приведения совпадает с центром масс.
24. Работа и мощность системы сил. Мощность момента пары сил. Кинетическая энергия системы материальных точек. Момент инерции системы материальных точек относительно оси. Теорема об изменении кинетической энергии.
25. Кинетическая энергия для простейших движений абсолютно твердого тела. Момент инерции системы материальных точек относительно оси. Теорема Кенига для произвольного движения системы материальных точек.
26. Консервативные системы. Силовая функция, потенциальная энергия, потенциальные силы. Теорема о приращении кинетической энергии для консервативных систем. Полная механическая энергия. Закон сохранения полной механической энергии системы материальных точек для потенциальных сил.
27. Понятие связей, наложенных на механическую систему. Примеры связей. Уравнения связей. Классификация связей. Возможные перемещения и возможные скорости точек механической системы, допускаемые связями. Примеры.
28. Силы реакций связей. Аксиома освобождаемости от связей. Идеальные связи. Примеры.
29. Число степеней свободы механической системы, обобщенные координаты и обобщенные скорости. Примеры.
30. Обобщенные силы. Обобщенные силы реакции идеальных связей.
31. Даламберовы силы инерции. Принцип Даламбера-Лагранжа.
32. Принцип Даламбера-Лагранжа для систем с идеальными удерживающими связями. Принцип возможных перемещений. Условие равновесия системы с идеальными голономными стационарными связями.
33. Тождества Лагранжа. Дифференциальные уравнения движения механической системы с идеальными связями (уравнения Лагранжа второго рода).
34. Уравнения Лагранжа второго рода для потенциальных сил. Функция Лагранжа. Уравнения равновесия консервативных механических систем с идеальными голономными связями.
35. Уравнения плоскопараллельного движения абсолютно твердого тела.
БИЛЕТ 1.
Кинематика— это часть механики, которая занимается изучением движения материальных тел, не интересуясь причинами возникновения этого движения (с геометрической точки зрения).
Движение— изменение положения.
— радиус-вектор точки M.
— векторный закон движения точки.
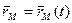
Материальная точка— тело, размерами которого можно принебречь. Это модель.
— принимаем за неподвижную. 
— едничные вектора.
— движение задано координатным способом.
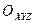
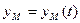
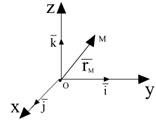
Скорость точки при векторном и координатном способе задания движения.
, 
— средняя скорость за 
, 
— мгновенная скорость.
(1)
не изменяются, так как — принимаем за неподвижную.
(2)
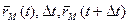
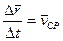
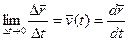
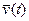
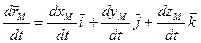
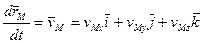
Сравниваем (1) и (2)
, 
, 
.
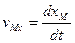
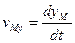
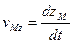
При координатном способе задания движения материальной точки вектор скорости определяется своими проекциями на оси координат, являющиеся неподвижными.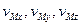 
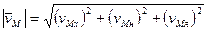
. Эти проекции скорости равны производным от соответствующих координат. Знание проекций скорости позволяет найти ее величину и ее направление.
.
Направление вектора скорости можно задать с помощью углов, которые образуют вектор скорости с координатными осями.
, 
, 
Положение 
стремится к касательной точки. Скорость в каждый момент времени направлена по касательной к траектории.
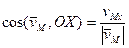
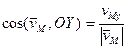
Источник
Векторный способ задания движения точки
Введение
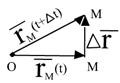
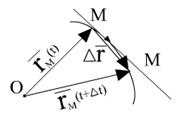
Положение точки однозначно определяется заданием ее радиус-вектора , который изменяется со временем при движении точки. При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.
Например, для точки, движущейся с постоянным ускорением , радиус-вектор определяется одной векторной формулой:
,
где – постоянные векторы, не зависящие от времени. Применяя формулы, мы можем найти кинематические величины в векторном виде, не зависимо от выбранной системы координат.
При координатном способе задания движения, мы выбираем систему координат, и в ней задаем зависимости координат точки от времени . Таким образом, координатный способ привязан к выбранной системе координат, а векторный способ не зависит от системы координат.
Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.
Основные формулы при векторном способе задания движения
Скорость точки
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.
Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.
Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.
Скорость точки направлена по касательной к траектории. Пусть – единичный вектор в направлении касательной. Тогда скорость может быть направленной либо вдоль вектора :
,
либо в противоположную сторону:
.
Чтобы охватить эти два случая, вводят алгебраическую величину скорости :
.
Это скалярная величина, равная по абсолютной величине модулю скорости, но она может принимать как положительные, так и отрицательные значения:
.
При , вектор скорости сонаправлен с . При он направлен в противоположную сторону. Величина является проекцией вектора скорости на направление . Поскольку – это единичный вектор, то
.
Единичный вектор в направлении касательной к траектории:
.
Ускорение точки
Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.
Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.
Тангенциальное ускорение
Алгебраическая величина тангенциального ускорения – это скалярная величина, равная проекции полного ускорения на направление единичного вектора , касательного к траектории:
.
Тогда вектор тангенциального ускорения можно записать в следующем виде:
.
Величина может быть как положительной, так и отрицательной. При положительном , вектор касательного ускорения сонаправлен с единичным вектором . При отрицательном – вектор касательного ускорения направлен в противоположную сторону. Модуль равен модулю касательного ускорения:
.
Алгебраическая величина тангенциального ускорения равна производной по времени от алгебраической величины скорости:
.
Производная по времени модуля скорости:
.
Если между векторами скорости и ускорения острый угол, то движение ускоренное. Если между ними тупой угол, то движение замедленное.
Нормальное ускорение
Вектор нормального ускорения:
.
; .
Единичный вектор в направлении главной нормали траектории:
.
Вектор перпендикулярен вектору и направлен к центру кривизны траектории. Нормальное ускорение всегда направлено к центу кривизны траектории. Поэтому, если выразить его через единичный вектор главной нормали:
,
то . Поэтому .
Модуль нормального ускорения равен проекции полного ускорения на направление главной нормали:
.
Имеют место следующие формулы:
.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 06-03-2016 Изменено: 29-01-2020
Источник
