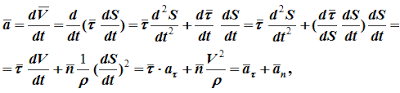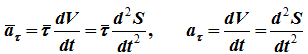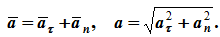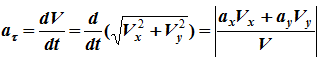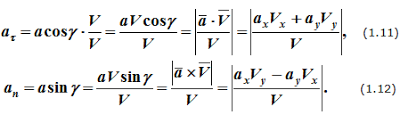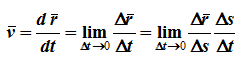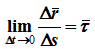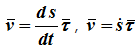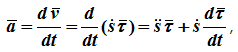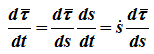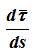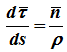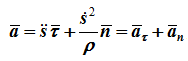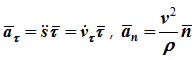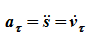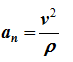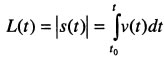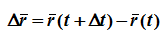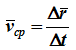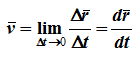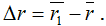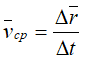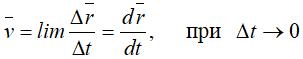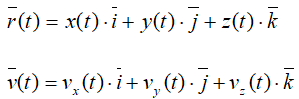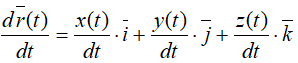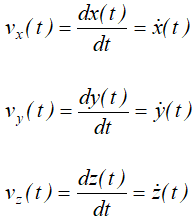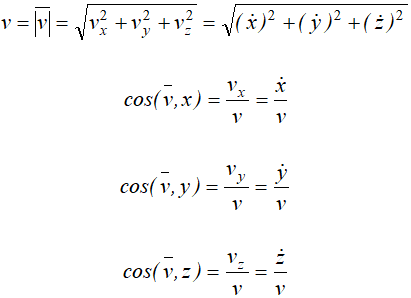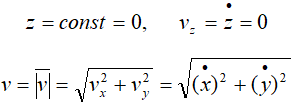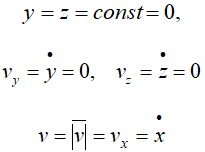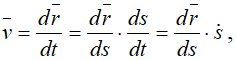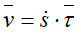Скорость точки при естественном способе задания движения это

iSopromat.ru

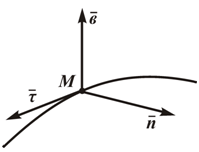
При естественном способе задания движения точки предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

• τ — орт касательной;
• n — орт нормали;
• b — орт бинормали;

Единичные орты τ, n, b определяют направление соответствующих осей в каждой точке кривой.

Чтобы задать закон движения точки естественным способом необходимо:

1. знать траекторию движения;
2. установить начало отсчета на этой кривой;
3. установить положительное направление движения;
4. дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t).

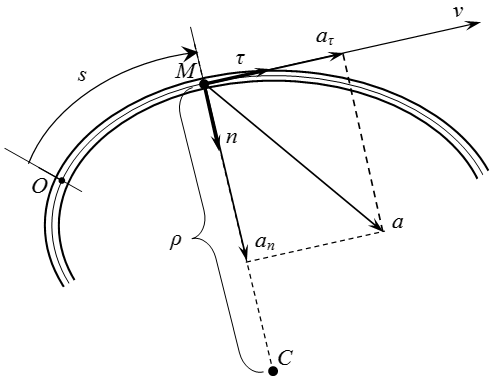
Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

Скорость и ускорение точки

Скорость точки при естественном способе задания её движения определяется по формулам

Первая формула определяет величину и направление вектора скорости, вторая формула только величину.

Ускорение определяется как производная от вектора скорости:

оно характеризует быстроту изменения величины скорости точки;

Нормальное ускорение точки

характеризует быстроту изменения направления вектора скорости;

ρ — радиус кривизны траектории в данной точке (например, для окружности: ρ = R, для прямой линии ρ = ∞).

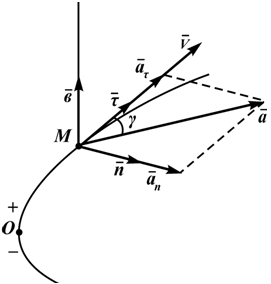
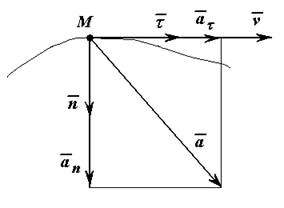
Полное ускорение точки при естественном способе задания движения определяется следующим образом (рисунок 1.5):

Ранее отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому, например, от координатного к векторному. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.

Далее, для естественнго способа задания движения точки, получаем

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Рассмотрим определение скорости и ускорения точек при естественном способе задания движения:

— единичный вектор касательной, тогда

Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени.

Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.

поскольку τ — переменный по направлению вектор, то:

определяется только свойствами траектории в окрестности данной точки, при этом

n — единичный вектор главной нормали,
ρ — радиус кривизны траектории в данной точке.

т.е. вектор ускорения раскладывается на две составляющие — касательное и нормальное ускорения:

• алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Естественный способ задания движения точки

Введение

Естественный способ задания движения материальной точки применяется в тех случаях, когда траектория заранее известна. Например, точка движется внутри желоба в твердом теле. В этом случае мы, произвольным образом, выбираем некоторую неподвижную точку на траектории. Эту точку мы принимаем за начало отсчета. Далее мы произвольным образом выбираем положительное направление. Рассмотрим подвижную точку на траектории. Пусть – расстояние от точки до точки , измеренное вдоль дуги траектории. Введем криволинейную координату следующим образом. Если точка находится в положительном направлении относительно начала отсчета , то . Если точка находится в отрицательном направлении относительно начала отсчета , то . Тогда криволинейная координата однозначно определяет положение точки на траектории. При движении точки, координата изменяется со временем :
.

Таким образом, при естественном способе задания движения материальной точки, мы задаем следующие данные:
1) траекторию точки;
2) начало отсчета с указанием положительного и отрицательного направления отсчета;
3) криволинейную координату, как функцию от времени: .

Определение кинематических величин

В начале мы должны определить геометрические характеристики траектории – касательную, главную нормаль и радиус кривизны.

По заданной траектории, для любого положения точки, мы можем определить единичный вектор , направленный по касательной к траектории; единичный вектор , направленный вдоль главной нормали (к центру кривизны) траектории и радиус кривизны траектории. Поскольку вектор можно направить по касательной двумя взаимно противоположными способами, то мы направим вектор вдоль направления, которое мы приняли за положительное. Вектор можно направить только одним способом – к центру кривизны траектории. Векторы и представляют собой два орта естественного трехгранника. В простых случаях, найти векторы , и радиус кривизны траектории можно геометрическим способом (см. пример решения задачи ниже). Как найти эти величины в более сложных случаях, указано на странице “Оси естественного трехгранника”. Там же приводится пример определения векторов , и радиуса кривизны траектории для винтовой линии.

После того, как мы определили орты естественного трехгранника , и радиус кривизны траектории , мы можем найти векторы скорости и ускорения точки . Выводы представленных ниже формул даны на странице “Кинематика материальной точки”.

Дифференцируя по , находим проекцию скорости на вектор :
.
Модуль скорости:
.
Вектор скорости:
.
Скорость, как и следовало, направлена по касательной к траектории. Если скорость направлена в положительном направлении, то
.
Если скорость направлена в отрицательном направлении, то
.

Дифференцируя по , находим тангенциальное ускорение (проекцию ускорения на вектор ):
.
Вектор тангенциального ускорения:
.
Нормальное ускорение:
.
Вектор нормального ускорения:
.
Вектор полного ускорения:
.
Модуль полного ускорения:
.

Пример решения задачи

Точка движется по дуге окружности радиуса по закону

( s – в метрах, t – в секундах), где – расстояние от до , измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени . Изобразить на рисунке векторы и , считая, что точка в этот момент находится в положении , а положительное направление отсчета – от к .

Определим положение точки в момент времени .
.
Пусть – центр окружности. Угол между векторами и :
.
По условию, положительное направление – от к , то есть слева направо. Поскольку , то точка расположена слева от точки .

Дифференцируя по , находим проекцию скорости на направление касательной к траектории:
.
В момент времени :
.
Поскольку , то вектор скорости направлен по касательной к траектории в сторону возрастания . Абсолютное значение (модуль) скорости:
.

Дифференцируя по , находим касательное ускорение точки:

.
В момент времени :
.
Поскольку , то вектор касательного ускорения направлен по касательной к траектории в сторону возрастания .

Нормальное ускорение:
.
Вектор направлен к центру окружности.

Автор: Олег Одинцов . Опубликовано: 09-04-2016

Источник

Скорость точки при естественном способе задания движения это

3) Скорость и ускорение точки при естественном способе задания движения.

Если траектория точки известна (т.е. в некоторой системе отсчета определена графически, с помощью уравнения или другим образом), то задать движение точки можно естественным способом. Для этого необходимо: зафиксировать на трактории точку начала отсчета, выбрать положительное и отрицательное направления отсчета дуговой координаты и указать уравнение движения точки по траектории в виде S=S(t).

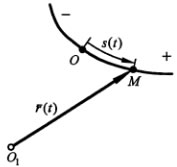
Скалярный параметр S в данном случае имеет смысл криволинейной (дуговой) координаты, модуль которой определяет текущее расстояние по траектории от начала отсчета (точки О) до подвижной точки М, а знак показывает, по какую сторону от начала отч=счета находится точка М на траектории.

Следует отметить, что уравнение движения в форме S=S(t) определяет текущее положение точки именно на траектории, при этом может быть установлена взаимно однозначная связь между значениями координаты S и радиус-вектором точки М в той системе отсчета, в которой определена в рассматриваемом случае траектория движения точки. Тогда радиус-вектор точки может быть представлен в виде функциональной зависимости от параметра S в виде r=r(S).

Модуль скорости, т.е. ее численное значение, при естественном способе задания движения точки определятся так: .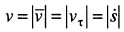

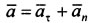
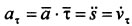
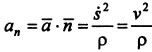
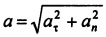
Ускорение составляет сумму касательной и нормальной составляющих: , где и . Следовательно: .

Дополнение: Значение пути —

Источник

iSopromat.ru

Скоростью точки называют кинематическую меру ее движения, равную производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.

Скорость относительно выбранной системы отсчета это одна из основных характеристик движения точки.

Вектор скорости направлен по касательной к траектории точки в сторону движения.

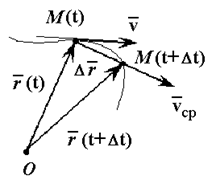
Рассмотрим перемещение точки за малый промежуток времени Δ t:

средняя скорость точки за промежуток времени D t.

Наш видеоурок по теме:

Скорость точки в данный момент времени

Скорость точки при векторном способе задания движения

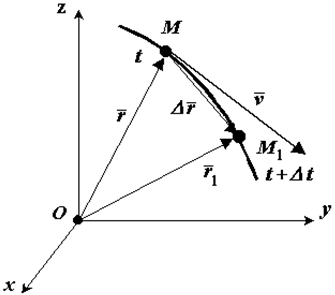
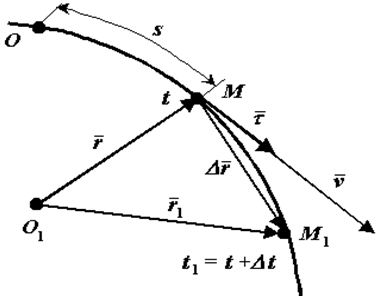
Положение движущейся точки М относительно системы отсчета в момент времени t₁ определяется радиус-вектором r.

В другой момент времени t₁=t+Δt точка займет положение М₁ с радиус-вектором r₁.

За время Δt радиус-вектор движущейся точки изменится на

Средней скоростью v_ср называется отношение изменения радиус-вектора Δr к изменению времени Δt.

Скорость точки равна первой производной по времени от ее радиус-вектора.

Скорость точки при координатном способе задания движения

Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим

Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.

Модуль скорости и направляющие косинусы равны:

Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:

Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда

Скорость точки при естественном способе задания движения

Пусть скорость точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).

Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O₁

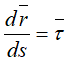
— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.

При ds>0 направления векторов τ и dr совпадают.

Если точка движется в сторону убывающих расстояний, то ds

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник