- Скорость способы измерения величины
- Новый Эталон Килограмма
- Солнце Становится Ближе
- Человек «Искрививший» Время
- Что за Очки у Будущего?
- Скорость. Единицы скорости
- Содержание
- Скорость при равномерном движении
- Как вычислить скорость
- Скорость при неравномерном движении
- Единицы измерения скорости
- Скорость как вектор
- Примеры задач на нахождение скорости
- Классификация методов измерения скорости.
Скорость способы измерения величины
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый. »»»
Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory. »»»
Человек «Искрививший» Время
биография Альберта Эйнштейна — величайшего физика создавшего «Общую теорию относительности». »»»
Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора. »»»
Одним из способов определения скорости или ускорения движущегося тела является измерение через равные промежутки времени, отсчитанные секундомером или электронным таймером длины пути по траектории движения. Пройденное расстояние, поделенное на затраченное время,— это средняя скорость для каждого участка пути. Ускорение может быть вычислено по разности в скоростях, подсчитанных для двух различных участков на пути движения тела, деленной на временной интервал между этими двумя участками.
Другим способом определения скорости или ускорения является присоединение телеграфной ленты к движущемуся телу. Движущееся тело протягивает ленту через телеграфный аппарат — таймер, как показано на рисунке.
Магнитное поле катушки заставляет колебаться стальную полоску таймера с частотой 50 раз в секунду, которая оставляет черные точки на белой бумажной ленте, движущейся под копировальным диском. Каждая последующая пара точек представляет временной интервал 1/50 с (0,02 с) вне зависимости от того, на сколько будут отстоять эти точки друг от друга. Замеренное расстояние между любыми двумя последующими точками — это расстояние, которое прошло тело за 0,02 с. Поскольку лента фиксирует и пройденное расстояние, и затраченное на это время, го полученные данные позволяют подсчитать скорость.
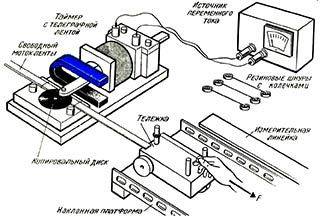
Можно составить своеобразную таблицу, если разрезать ленту на полоски и приклеить их на разграфленную бумагу. Каждая полоска должна охватывать одинаковый временной интервал, например десять отрезков представляют 0,2 с. Длина первой ленты — это расстояние, пройденное за 0,2 с, и, таким образом, средняя скорость на этом расстоянии определяется делением длины ленты на 0,2 с.
Источник
Скорость. Единицы скорости
Содержание
Механическое движение имеет множество характеристик. Вы уже узнали, что оно относительно и бывает разных видов: прямолинейное и криволинейное, равномерное и неравномерное.
Тела движутся по воображаемым линиям, которые называются траекториями, а длина траектории – это путь, который проходит тело.
В этом уроке мы рассмотрим новую физическую величину, характеризующую движение – скорость.
Скорость при равномерном движении
Взгляните на рисунок 1. Если мы предположим, что бегуны, велосипедисты и автомобили двигаются равномерно, то чем будет отличаться их движение?
Рисунок 1. Разные физические тела, совершающие равномерное движение.
В таких случаях обычно мы говорим, что машина будет двигаться быстрее, чем велосипедист, а велосипедист – быстрее, чем бегун. Здесь, в физике, появляется такая величина, как скорость.
Скорость – это физическая величина, характеризующая быстроту движения тел
В нашем случае люди пробегают 15 км за 1 час, велосипедисты проезжают 25 км за 1 час, а машина за то же время – 60 км, т.е. движутся с различными скоростями.
Скорость при равномерном движении тела показывает, какой путь проходит тело в единицу времени
Скорость при равномерном движении постоянна
Как вычислить скорость
Чтобы определить скорость при равномерном движении, нужно путь, пройденный телом за выбранный промежуток времени, разделить на этот промежуток времени:
$$\upsilon = \large \frac
где $\upsilon$ – скорость, $S$ – путь, $t$ – время.
Cкорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое пройден этот путь.
Соответственно, если автомобиль проезжает в течение 10 с путь, равный 20 метрам, то его скорость будет равна $\frac<20 м> <10 с>= 2 \frac<м><с>$ (2 метра в секунду).
Скорость при неравномерном движении
При неравномерном движении тело проходит разные пути за равные промежутки времени, т.е. скорость тела изменяется от одного участка пути к другому.
Как же определить скорость на всем пути? Здесь нам поможет понятие средней скорости.
Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на все время движения:
Отметим, что средняя скорость описывает движение тела за весь промежуток времени. В это время тело можно замедляться, разгоняться, останавливаться.
Например, если вы выезжаете на автомобиле из Москвы в Санкт-Петербург (рисунок 2), то весь путь займет у вас 10 ч. В это время машина будет то набирать скорость, то тормозить, сделает остановку. Общий путь, который вы при этом проедите, будет равен 600 км.
Средняя скорость движения автомобиля будет равна:
$\upsilon_ <ср>= \frac
Рисунок 2. Пример неравномерного движения.
Взгляните на таблицу 1, где приведены различные средние скорости.
| Тело | Скорость | Тело | Скорость |
|---|---|---|---|
| Улитка | 0,0014 | Пассажирский самолет | 220 |
| Черепаха | 0,05-0,14 | Звук в воздухе при $0 \degree C$ | 332 |
| Муха | 5 | Пуля автомата Калашникова | 760 |
| Пешеход | 1,5 | Луна вокруг Земли | 1000 |
| Конькобежец | 13 | Молекула водорода при $0 \degree C$ | 1693 |
| Скворец | 20 | Молекула водорода при $25 \degree C$ | 1770 |
| Страус | 22 | Земля вокруг Солнца | 30 000 |
| Автомобиль | 20 | Свет и радиоволны | 300 000 000 |
Средние скорости движения некоторых тел, скорость звука, радиоволн и света, $\frac<м><с>$.
Единицы измерения скорости
В Международной системе (СИ) скорость измеряется в метрах в секунду $\frac<м><с>$.
За за единицу скорости принимают скорость такого равномерного движения, при котором за 1 секунду тело проходит путь длиной 1 метр.
Следственно, скорость в системе СИ – количество метров, которое тело пройдёт за 1 секунду.
В повседневной жизни мы чаще видим, что скорость измеряют в километрах в час $\frac<км><ч>$. Также можно использовать километры в секунду $\frac<км><с>$ и сантиметры в секунду $\frac<см><с>$.
Наиболее часто встречаемое ограничение скорости в городах – $ 60 \frac<км><ч>$. Переведем это значение в $\frac<м><с>$:
Так мы увидели, что числовое значение скорости зависит от выбранной единицы измерения.
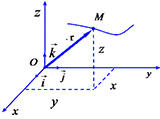
Скорость как вектор
Логично, что, кроме числового значения, скорость имеет и направление. Например, чтобы узнать, где будет находиться велосипедист через 1 час после того, как он выехал из дома, нам необходимо знать скорость движения и ее направление.
Физические величины делятся на те, которые имеют направление и те, которые его не имеют – на векторные и скалярные:
1. Векторные величины – это величины, которые, кроме числового значения (модуля), имеют еще и направление.
Скорость – это векторная физическая величина
Векторные величины обозначаются буквами со стрелочками. Скорость обозначается как $\vec<\upsilon>$, а модуль скорости – $\upsilon$.
На рисунке 3 стрелкой показано направление скорости (направление движение тела).
Рисунок 3. Направление скорости для различных тел.
2. Скалярные величины – это физические величины, которые не имеют направления и характеризуются только числовым значением. Это путь, объем, время, длина, масса и др.
Примеры задач на нахождение скорости
1. Равномерно двигаясь, поезд за 3 часа прошел путь длиной 152 км. Найдите скорость движения поезда в единицах СИ.
Дано:
$S = 152 км$
$t = 3 ч$
Найти:
$\upsilon -?$
Показать решение и ответ
Решение:
$\upsilon = \frac
$\upsilon = \frac<152> <3>\frac<км> <ч>\approx 51 \frac<км> <ч>$.
Выразим в единицах СИ:
$51 \frac<км> <ч>= \frac<51 000> <3600>\frac<м>
Ответ: $\upsilon = 14 \frac<м><с>$.
2. Скорость лыжника первую часть пути составляла $20 \frac<км><ч>$ в течение 15 мин. Следующие 45 мин его скорость была $10 \frac<км><ч>$. Найдите среднюю скорость лыжника.
Обозначим первую часть пути как $s_1$, вторую как $s_2$. Время, соответствующее движению на этих участках, $t_1$ и $t_2$ (рисунок 4). Скорости – $\upsilon_1$ и $\upsilon_2$.
Рисунок 4. Схема движения лыжника.
Дано:
$\upsilon_1 = 20 \frac<км><ч>$
$t_1 = 15$ мин
$\upsilon_2 = 10 \frac<км><ч>$
$t_2 = 45$ мин
Найти:
$\upsilon_ <ср>-?$
Показать решение и ответ
Решение:
Скорость лыжника на первой и второй частях пути:
$\upsilon_1 = \frac
Выразим из этих уравнений неизвестные $s_1$ и $s_2$:
$s_1 = \upsilon_1t_1$; $s_2 = \upsilon_2t_2$
Чтобы найти среднюю скорость лыжника, нужно его полный путь разделить на все время движения:
$\upsilon_ <ср>= \frac
Выпишем отдельно часть выражения и переведем в часы:
$t_1+t_2 = 15$ мин $+$ $45$ мин = $1$ ч.
Тогда:
$t_1 = \frac<1><4>$ ч $= 0,25$ ч
$t_2 = \frac<3><4>$ ч $= 0,75$ ч
Ответ: $\upsilon_ <ср>= 12,5 \frac<км><ч>$.
Источник
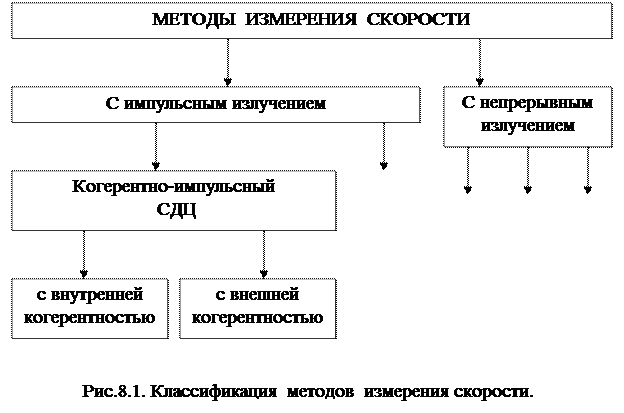
Классификация методов измерения скорости.
Измерение скорости перемещения объекта (цели) относительно РЛС или относительно земной поверхности в радиолокации основано на использовании эффекта Доплера и сводится к измерению доплеровского приращения частоты отраженного от цели сигнала.
В активной радиолокации, т.е. с учетом двухстороннего распространения сигнала до цели и обратно доплеровское приращение частоты равно:
где: Vr – радиальная скорость цели (скорость изменения дальности до цели) относительно РЛС.
Отсюда видно, что доплеровская частота FV тем выше, чем больше радиальная скорость перемещения цели Vr и чем короче длина волны λ РЛС. Следовательно, по изменению частоты принимаемого сигнала можно судить о радиальной скорости цели.
Наиболее просто измерение скорости цели может быть произведено при излучении непрерывного немодулированного когерентного сигнала, т.е. непрерывного синусоидального колебания с неизменной начальной фазой.
При применении непрерывных зондирующих сигналов благодаря их большой длительности удается значительно проще, чем при импульсных сигналах, осуществить разрешение целей по частоте (радиальной скорости) и наиболее полно использовать энергию сигнала. Однако применение непрерывного зондирующего сигнала связано с известными техническими трудностями по разделению приемного и передающего каналов.
Кроме того, при установке на борту объекта (например, на самолете, ракете и т.д.) такие системы измерения скорости сильно подвержены влиянию помех, вызванных вибрациями объекта. Поэтому для измерения скорости целей, как правило, применяют РЛС с частотной модуляцией непрерывного зондирующего сигнала или РЛС с импульсным излучением.
Классификация методов измерения скорости приведена на рис.8.1.
Разрешающая способность по частоте (радиальной скорости).
Разрешающая способность по частоте равна минимальному частотному сдвигу, при котором возможно раздельное измерение частоты отраженных сигналов, принятых от двух целей. В теории сигналов доказывается, что разрешающая способность по частоте (радиальной скорости) зависит от длительности сигнала TSи составляет величину, обратно пропорциональную длительности сигнала:
δF = 1/TS
Физическая сущность этого свойства следует из определения частоты колебания, как числа его полных периодов в единицу времени. Это означает, что частота колебания может быть зарегистрирована при времени наблюдения, длительность которого не меньше одного периода этого колебания. Аналогично, чтобы зафиксировать различие двух частот колебаний, необходима длительность сигнала TS, не меньшая периода разностной частоты.
Разрешающую способность по радиальной скорости цели можно получить, используя зависимость радиальной скорости цели от частоты Доплера.
δVr =δFλ/2 =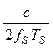 
,
где: fS – частота зондирующего сигнала.
Источник
