Сочетания с повторениям
Ответ: 2520 перестановок.
Пример 2.4: Сколькими способами можно расселить 8 студентов по 3 комнатам: одноместной, трехместной и четырехместной?
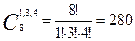
Ответ: 280 способов.
§3. Размещения
Рассмотрим теперь такие перестановки из n различных элементов, в которых участвуют не все, а только определенное количество элементов.
Определение 3.1:Размещенияминазывают комбинации, составленные из n различных элементов по k элементам, которые различаются либо составом элементов, либо их порядком.
Число всех возможных размещений определяют по формуле:

Пример 3.1: Сколькими способами из 7 книг можно отобрать 3 и расставить их на 3 места на книжной полке?
1 способ. n = 7, k =3.

2 способ. Эту задачу можно также решить по принципу произведения.
Книги должны занять 3 места. На 1 место можно поставить любую из 7 книг, на 2 место – любую из оставшихся 6, а 3 место может заполнить любая из оставшихся 5 книг. Таким образом, общее количество способов равно 7*6*5=210.
Ответ: 210 способов.
Пример 3.2: Определить количество телефонных номеров, состоящих из 5 различных цифр.
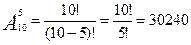
Ответ: 30240 телефонных номеров.
Размещения с повторениями.
Если каждый из k элементов упорядоченного множества может быть выбран n способами, независимо от других, то число способов выбора всех k элементов вычисляется по формуле:
Пример 3.3: В НИИ работает 4 курьера А, В, С, D. Сколько существует способов рассылки 7 писем в 7 различных организаций, если доставка писем осуществляется только курьерами, работающими в НИИ?

Ответ: 16384 способа.
Пример 3.4: В кабину лифта 9-этажного здания вошло 3 пассажира A, B, C, каждый из которых может выйти на любом из 8 этажей. Сколькими способами может осуществиться разгрузка лифта?

Ответ: 512 способов.
§4. Сочетания
Определение 4.1.:Сочетанияминазываюткомбинации, составленные из n различных элементов по k элементам, которые отличаются хотя бы одним элементом.
Число сочетаний определяется по формуле:

Замечание 4.1. Разница между размещениями и сочетаниями состоит в том, что в размещениях порядок элементов учитывается, а в сочетаниях – нет.
Пример 4.1.: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
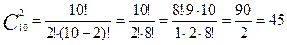
Ответ: 45 способов.
Пример 4.2.: Сколькими способами можно составить комиссию из 3 х человек, выбирая их из 4 х супружеских пар, если:
а) в комиссию могут входить любые трое из данных 8 человек;
б) комиссия должна состоять из двух женщин и одного мужчины?
а) В комиссии не играет роли порядок членов, поэтому
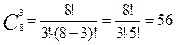
б) двух женщин можно отобрать 


Ответ: 24 способами.
Сочетаниями из n элементов по k элементов с повторениями называются группы, содержащие k элементов, причём каждый элемент принадлежит одному из n типов. Число различных сочетаний из n элементов по k элементам с повторениями вычисляется по формуле:
Пример 4.3.: В кондитерской продаются пирожные 5 видов: бисквитные, корзиночки, буше, эклеры, трубочки. Сколькими способами можно купить 12 пирожных?

Ответ: 4368 способов.
ГЛАВА 5. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ.
§1. Основные понятия
Определение 1.1.Граф G, по существу,есть набор из 2 х множеств любой природы – непустого множества вершин V и множества ребер E , причем каждому ребру соответствуют две концевые вершины, которые, вообще говоря, могут и совпадать.
Определение 1.2. Вершина,соединенная ровно с одним ребром,исамо это реброназываютсяконцевыми или висячими.
Определение 1.3.Различные ребра, соединяющие две вершины, называются кратнымиили параллельными.
Определение 1.4.Ребра с совпадающими концами называютсяпетлями.
Определение 1.5.Граф G, имеющий n вершин, часто называютn – графом;если, кроме того, G содержит m ребер, то G – (n,m) граф.
Определение 1.6. Если e = uv некоторое ребро данного графа, то вершины u, v называются смежными.
Определение 1.7. Ребро e и вершина v инцидентны, если v – концевая вершина для e.
Определение 1.8. Ребра e и f называются смежными, если они имеют общую концевую вершину.
Определение 1.9. Две вершины, инцидентные одному и тому же ребру, называются соседними или смежными.
Определение 1.10. Степенью вершины v называется число ребер, инцидентных этой вершине, причем любая вершина учитывается дважды. Обозначение: degGv или deg v.
Определение 1.11. Граф H называют подграфом графа G, если VHÍVG и EHÍEG.
Определение 1.12. Если VH=VG, то подграф H называется остовным подграфом.
Определение 1.13.Ориентированным графом G или орграфом G называется тройка (V, E, j), где j:E®V 2 =V´V, ставящего в соответствие каждому элементу eÎE упорядоченную пару элементов v1v2ÎV, называемых концами ребра e.
Определение 1.14. Если j(e)=v1v2 – упорядоченная пара, т.е. v1v2¹v2v1, то ребро e называется ориентированной дугой, исходящей из вершины v1 и входящей в вершину v2; v1называется началом дуги e, а v2 – концом дуги. Если j(e)=v1v2— неупорядоченная пара, то ребро e называется неориентированным.
§2. Способы задания графов
1) Перечисление. Список ребер графа с указанием их концов и добавлением списка изолированных вершин.
2) Матрица соседства (смежности) вершин графа G.
Пусть G – любой n-граф. Упорядочим множество вершин графа VG=
Определим матрицу смежности B графа G. B – квадратная матрица размерности n, строки и столбцы которой соответствуют вершинам графа, причем неотрицательный элемент bij равен числу ребер, идущих из вершины vi в вершину vj ( вообще говоря, bij¹bji, однако для неориентированных графов матрица соседства симметричная). Для несмежных вершин соответствующий элемент матрицы равен 0. При i=j каждую петлю учитываем дважды.


Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Сочетания с повторениям
Ответ: 2520 перестановок.
Пример 2.4: Сколькими способами можно расселить 8 студентов по 3 комнатам: одноместной, трехместной и четырехместной?
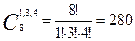
Ответ: 280 способов.
§3. Размещения
Рассмотрим теперь такие перестановки из n различных элементов, в которых участвуют не все, а только определенное количество элементов.
Определение 3.1:Размещенияминазывают комбинации, составленные из n различных элементов по k элементам, которые различаются либо составом элементов, либо их порядком.
Число всех возможных размещений определяют по формуле:

Пример 3.1: Сколькими способами из 7 книг можно отобрать 3 и расставить их на 3 места на книжной полке?
1 способ. n = 7, k =3.

2 способ. Эту задачу можно также решить по принципу произведения.
Книги должны занять 3 места. На 1 место можно поставить любую из 7 книг, на 2 место – любую из оставшихся 6, а 3 место может заполнить любая из оставшихся 5 книг. Таким образом, общее количество способов равно 7*6*5=210.
Ответ: 210 способов.
Пример 3.2: Определить количество телефонных номеров, состоящих из 5 различных цифр.
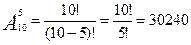
Ответ: 30240 телефонных номеров.
Размещения с повторениями.
Если каждый из k элементов упорядоченного множества может быть выбран n способами, независимо от других, то число способов выбора всех k элементов вычисляется по формуле:
Пример 3.3: В НИИ работает 4 курьера А, В, С, D. Сколько существует способов рассылки 7 писем в 7 различных организаций, если доставка писем осуществляется только курьерами, работающими в НИИ?

Ответ: 16384 способа.
Пример 3.4: В кабину лифта 9-этажного здания вошло 3 пассажира A, B, C, каждый из которых может выйти на любом из 8 этажей. Сколькими способами может осуществиться разгрузка лифта?

Ответ: 512 способов.
§4. Сочетания
Определение 4.1.:Сочетанияминазываюткомбинации, составленные из n различных элементов по k элементам, которые отличаются хотя бы одним элементом.
Число сочетаний определяется по формуле:

Замечание 4.1. Разница между размещениями и сочетаниями состоит в том, что в размещениях порядок элементов учитывается, а в сочетаниях – нет.
Пример 4.1.: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
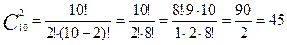
Ответ: 45 способов.
Пример 4.2.: Сколькими способами можно составить комиссию из 3 х человек, выбирая их из 4 х супружеских пар, если:
а) в комиссию могут входить любые трое из данных 8 человек;
б) комиссия должна состоять из двух женщин и одного мужчины?
а) В комиссии не играет роли порядок членов, поэтому
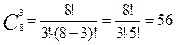
б) двух женщин можно отобрать 


Ответ: 24 способами.
Сочетаниями из n элементов по k элементов с повторениями называются группы, содержащие k элементов, причём каждый элемент принадлежит одному из n типов. Число различных сочетаний из n элементов по k элементам с повторениями вычисляется по формуле:
Пример 4.3.: В кондитерской продаются пирожные 5 видов: бисквитные, корзиночки, буше, эклеры, трубочки. Сколькими способами можно купить 12 пирожных?

Ответ: 4368 способов.
ГЛАВА 5. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ.
§1. Основные понятия
Определение 1.1.Граф G, по существу,есть набор из 2 х множеств любой природы – непустого множества вершин V и множества ребер E , причем каждому ребру соответствуют две концевые вершины, которые, вообще говоря, могут и совпадать.
Определение 1.2. Вершина,соединенная ровно с одним ребром,исамо это реброназываютсяконцевыми или висячими.
Определение 1.3.Различные ребра, соединяющие две вершины, называются кратнымиили параллельными.
Определение 1.4.Ребра с совпадающими концами называютсяпетлями.
Определение 1.5.Граф G, имеющий n вершин, часто называютn – графом;если, кроме того, G содержит m ребер, то G – (n,m) граф.
Определение 1.6. Если e = uv некоторое ребро данного графа, то вершины u, v называются смежными.
Определение 1.7. Ребро e и вершина v инцидентны, если v – концевая вершина для e.
Определение 1.8. Ребра e и f называются смежными, если они имеют общую концевую вершину.
Определение 1.9. Две вершины, инцидентные одному и тому же ребру, называются соседними или смежными.
Определение 1.10. Степенью вершины v называется число ребер, инцидентных этой вершине, причем любая вершина учитывается дважды. Обозначение: degGv или deg v.
Определение 1.11. Граф H называют подграфом графа G, если VHÍVG и EHÍEG.
Определение 1.12. Если VH=VG, то подграф H называется остовным подграфом.
Определение 1.13.Ориентированным графом G или орграфом G называется тройка (V, E, j), где j:E®V 2 =V´V, ставящего в соответствие каждому элементу eÎE упорядоченную пару элементов v1v2ÎV, называемых концами ребра e.
Определение 1.14. Если j(e)=v1v2 – упорядоченная пара, т.е. v1v2¹v2v1, то ребро e называется ориентированной дугой, исходящей из вершины v1 и входящей в вершину v2; v1называется началом дуги e, а v2 – концом дуги. Если j(e)=v1v2— неупорядоченная пара, то ребро e называется неориентированным.
§2. Способы задания графов
1) Перечисление. Список ребер графа с указанием их концов и добавлением списка изолированных вершин.
2) Матрица соседства (смежности) вершин графа G.
Пусть G – любой n-граф. Упорядочим множество вершин графа VG=
Определим матрицу смежности B графа G. B – квадратная матрица размерности n, строки и столбцы которой соответствуют вершинам графа, причем неотрицательный элемент bij равен числу ребер, идущих из вершины vi в вершину vj ( вообще говоря, bij¹bji, однако для неориентированных графов матрица соседства симметричная). Для несмежных вершин соответствующий элемент матрицы равен 0. При i=j каждую петлю учитываем дважды.


Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник






