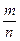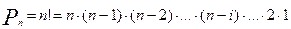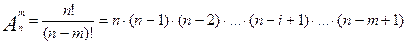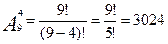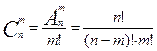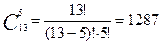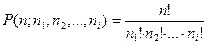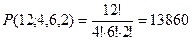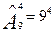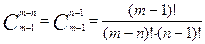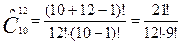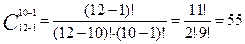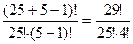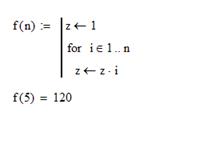Сколько существует способов рассадить 8 гостей за круглым столом

Сколько существует способов рассадить 8 гостей за круглым столом

В школьном курсе понятие «круговые перестановки» встречается в 7 классе в учебнике по алгебре в разделе «Для тех, кому интересно» [3].

В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить в ряд, или, как говорят математики, упорядочить, все элементы некоторого множества.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Получаемые при этом упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них элементов, называют перестановками без повторений из п элементовили «круговыми перестановками».

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют “сочетания”. В ХII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из п слогов. Как научная дисциплина, комбинаторика сформировалась в Х V II в. В книге “Теория и практика арифметики” (1656 г.) французский автор Андре Таке также посвящает сочетаниям и перестановкам целую главу.

Б. Паскаль в “Трактате об арифметическом треугольнике” и в “Трактате о числовых порядках” (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин “комбинаторика” стал употребляться после опубликования Лейбницем в 1665 г. работы “Рассуждение о комбинаторном искусстве”, в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги “Аг s соп j ес t ап d i” (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в ХIХ в [4].

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения. При решении задач на перестановки используется правило умножения.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Рассмотрим задачу: В турнире четверо участников. Сколькими способами могут быть распределены места между ними?

Будем рассуждать в соответствии с правилом умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье любой из двух оставшихся, а на четвертом месте останется последний участник. Значит, места между участниками могут быть распределены 4 ۰ 3 ۰ 2 ۰ 1 = 24 способами. Решив задачу, мы фактически подсчитали число перестановок для множества из четырех элементов. Рассуждая точно так же, можно показать, что для множества из пяти элементов число перестановок равно 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1, а для множества из десяти элементов это число равно 10 ۰ 9 ۰ 8 ۰ 7 ۰ б ۰ 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1.

Вообще если множество содержит п элементов, то число перестановок равно произведению п(п – 1)(п – 2) ۰…۰ 2 ۰ 1. Множители в этом произведении можно записать в обратном порядке: 1 ۰ 2 ۰ . ۰ (п – 2)(п – 1)п.

Такие произведения бывают очень длинными и часто выражаются огромными числами. Однако в математике есть специальный символ для их обозначения. Произведение всех натуральных чисел от 1 до п обозначают п! (читают: «п факториал»). Значение выражения п! можно найти для любого натурального числа п (при этом считают, что 1! = 1).

Факториалы растут удивительно быстро. Можно понаблюдать за их изменением, рассмотрев таблицу, в которой приведены факториалы чисел от 1 до 10:

Источник

Теоретическая часть

Лабораторная работа №1. Случайные события

«Классическое определение вероятности. Основные формулы комбинаторики».

Теоретическая часть.

Классическая схема позволяет вычислять вероятности без проведения случайного эксперимента, основываясь лишь на свойстве симметрии возможных исходов испытания, так что нет оснований считать какой-либо из исходов более вероятным, чем другой.

Определение: Вероятностью случайного события А, называется отношение числа m исходов, благоприятствующих событию А, к числу всех равновозможных исходов испытания, составляющих полную группу несовместных событий.

Р(А)=

При непосредственном подсчете вероятностей часто используют формулы комбинаторики. Простейшими из них являются перестановки, сочетания, размещения и разбиения.

Перестановки отличаются друг от друга только порядком входящих в них элементов. Количество перестановок из n элементов:

Пример 1: Сколькими способами можно рассадить 10 человек за круглым столом, если имеет значение только порядок соседей.

Отметим, что вращение людей вокруг стола не меняет их взаимного расположения, поскольку соседи справа и слева остаются прежними. Если место за столом уникально, то существует 10! Способов рассадить людей за столом. Существует 10 вращений вокруг стола, поэтому делим на 10 и получаем 9! Способов рассадить людей за круглым столом, если значение имеет только порядок соседей.

Пусть М – множество, состоящее из n элементов.

Размещением из n элементов по m или упорядоченной (n,m)– выборкой, называется любой кортеж, состоящий из m, попарно различных элементов множества М.

Число размещений из n по m элементов:

Пример 2: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9, если все цифры различны.

Сочетанием из n элементов по m или неупорядоченной (n,m)­­– выборкой, называется любое подмножество множества M, состоящее из m элементов.

Надо заметить, что количество сочетаний отличается от числа размещений количеством перестановок каждого сочетания, то есть

Пример 3: Сколько существует вариантов выбора 5 карт трефовой масти из колоды, состоящей из 54 карт.

В колоде имеется 13 треф, из которых выбирается 5, поэтому

Пусть множество М разбито на k таких различных типов, что имеется n₁ неразличимых объектов типа 1, n₂ неразличимых объектов типа 2, и, вообще, n_i неразличимых объектов типа i (i=1,2,3,…,k), тогда количество различных размещений элементов множества:

Пример 4: Сколькими способами можно расставить на полке 12 книг, из которых 4 одинаковых учебника по математике, 6 одинаковых по информатике, 2 одинаковых по химии.

Если трактовать повторения как возвращения объекта во множество М и повторное его использование, то возникает идея размещений и сочетаний с повторениями. Их количество можно вычислить по формулам:

– количество размещений из n элементов по m с повторениями.

– количество сочетаний из n элементов по m с повторениями.

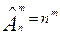
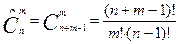
Пример 5: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9.

Так как нет ограничения на повторение цифр, то существует

Теорема: Если необходимо выбрать хотя бы по одному объекту из n по m с повторением, то количество различных сочетаний равно

Пример 6: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков.

Поскольку 12 пончиков выбираются из 10 видов с повторениями, то

Пример 7: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков, если необходимо выбрать хотя бы по одному пончику каждого вида .

Поскольку 12 пончиков выбираются из 10 видов с повторениями, то

Пример 8: Найдем количество различных решений уравнения

, где каждое слагаемое в левой части – неотрицательное число.

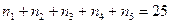
Это эквивалентно вопросу о том, сколько существует выборок вида

, где имеется объектов типа и

, но количество таких выборок — это количество различных сочетаний из 25 элементов по 5 элементов с повторениями. Итак, существуют

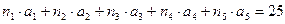
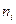
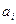
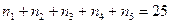
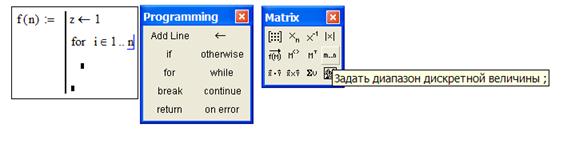
В среде MathCad нет встроенных функций для подсчета количества способов выбора объектов, поэтому необходимо воспользоваться возможностью программирования.

Чтобы создать программный модуль:

1. Введите выражение, которое будет находится слева от знака присваивания (имя функции);

2. Вызовите на экран панель Programming (программирование);

3. Нажмите на кнопку Add line[1] необходимое число раз;

4. В появившиеся местозаполнители введите необходимый программный код.

Для подсчета факториала необходимо организовать цикл. В среде MathCad это можно сделать с помощью оператора for и ранжирванной переменной, которая пробегает некоторое множество значений.

Фрагмент документа MathCad для подсчета факториала приведен ниже.

После того как программный модуль полностью определен и ни один из местозаполнителей ни остался пустым, функция может использоваться обычным образом.

Пример решения задачи на подсчет вероятности в среде МathCad:

Источник

Сколько существует способов рассадить 8 гостей за круглым столом

За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Пусть первой за стол сядет девочка, рядом с ней есть два места, на каждое из которых может сесть 8 человек, из которых только одна девочка. Таким образом вероятность, что девочки будут сидеть рядом равна

Приведём другое решение (перестановки).

Число способов рассадить 9 человек по девяти стульям равно Благоприятным является случай, когда на «первом» стуле сидит «первая» девочка, на соседнем справа сидит «вторая» девочка, а на остальных семи стульях произвольным образом рассажены мальчики. Поскольку выбрать «первую» девочку можно двумя способами, количество таких исходов равно А так как «первым» стулом может быть любой из девяти стульев (стулья стоят по кругу), количество благоприятных исходов нужно умножить на 9. Таким образом, вероятность того, что обе девочки будут сидеть рядом, равна

Приведём другое решение (круговые перестановки).

Напомним, что число способов, которыми можно расположить n различных объектов по n расположенным по кругу местам равно (n − 1)! Поэтому посадить за круглым столом 9 детей можно 8! способами. Объединим двух девочек в пару, это можно сделать двумя способами; рассадить по кругу 7 мальчиков и эту неделимую пару можно 7! способами. Тем самым, посадить детей требуемым образом можно 2 · 7! способами, поэтому искомая вероятность равна

Рассуждая аналогично, получим, что в общем случае для n девочек и m мальчиков, сидящих девочки с девочками, а мальчики с мальчиками, количество способов занять места за круговым столом равно n!m!, а вероятность случайной рассадки требуемым образом равна

Источник