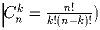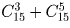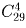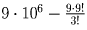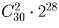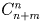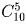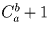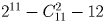Сколько способов выбрать два натуральных числа

Задача 1: Сколько квадратов со сторонами по линиям сетки можно нарисовать на доске 8 × 8?

Решение: 204

Задача 2: Сколько способов расставить n человек в ряд?

Решение: n!

Задача 3: Сколько способов выбрать a) двух человек из десяти?

b) трех человек из десяти?

c) k человек из n?

(Ответ: это число

Задача 4: Доказать, что .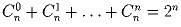

Задача 5: Сколько способов сделать бусы из a) семи разных бусинок b) пяти белых и двух черных бусинок (Бусы – это окружность, на которую насажены бусины. Ее можно поворачивать, но нельзя переворачивать).

Решение: а) 6! = 720; б) 3

Задача 6: Доказать, что 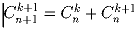a) по формуле b) с помощью комбинаторных рассуждений.

Задача 7: Доказать, что .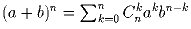

Задача 8: Сколько способов расставить на полку 3 книги одного вида, 5 – другого и 8 – третьего?

Задача 9: p – простое число. Доказать, что 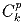делится на p.

Задача 10: Сколько способов разбить 12 человек на две группы по 12 и 5 человек так, чтобы:

a) два данных человека оказались в разных группах.

b) в одной группе?

Решение: а) 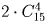; b)

Задача 11: a) Доказать, что число способов выбрать k человек из n и выбрать из них главного равно .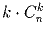

b) Доказать, что то же самое число равно .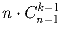

Задача 12: Сколько способов расставить 20 разных книг по 5 полкам?

Решение: 5²º

Задача 13: Сколько способов расставить 25 разных книг по 5 полкам так, чтобы на каждой было не менее одной книги?

Задача 14: Сколько способов расставить 25 одинаковых книг по 5 полкам (некоторые полки могут оказаться пустыми)?

Решение:

Задача 15: Сколько способов расставить на доске 8 × 8 a) 8 ладей b) 32 коня так, чтобы они не били друг друга?

Решение: а) 8!; б) 2.

Задача 16: Сколько всего 6-значных чисел

a) без единиц в записи.

b) по крайней мере с одной единицей в записи.

Решение: а) 8 9 5 ; b) 9 10 5 – 8 9 5

Задача 17: Сколько существует семизначных чисел, у которых

a) все цифры разные

b) любые две соседних цифры разные

c) есть две одинаковых цифры.

Решение: а) 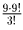; б)

Задача 18: Сколько способов рассадить 5 мужчин и 5 женщин за круглым столом так, чтобы мужчины и женщины чередовались?

Решение: 2 5! 5!

Задача 19: В классе 30 человек. Сколько способов разбить класс на две группы и в каждой выбрать старосту?

Решение:

Задача 20: Сколько 7-значных чисел, в которых

a) каждая цифра больше предыдущей?

b) каждая цифра не меньше предыдущей?

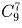
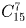
Решение: а) ; б) ;

Задача 21: Сколько способов разбить 15 мужчин и 15 женщин на пары для танцев?

Решение: 15!

Задача 22: Сколько разных слов можно составить из слова:

a) ПЕРЕЕЗД b) МАТЕМАТИКА c) АА … АББ … ББ (n букв «А», m букв «Б»)

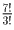
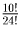
Решение: а) ; b) ; c)

Задача 23: Доказать тождества:

a) .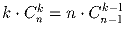

b) .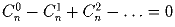

c) .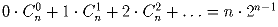

Задача 24: Сколько способов прочитать слово «ТРЕУГОЛЬНИК», двигаясь вправо и вниз:

Решение: a) 2¹º; б)

Задача 25: a) Круг разбит на простое число p секторов. Сколько способов раскрасить их в n цветов (раскраски, совмещающиеся при повороте, считаются одинаковыми).

b) Вывести из пункта a) малую теорему Ферма: n p – n делится на p.

Решение: .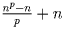

Задача 26: a,b – натуральные числа, a ≥ b – 1. Сколько способов расставить a белых и b черных фишек так, чтобы черные не стояли рядом?

Решение:

Задача 27: Доказать, что .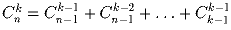

Задача 28: Пусть p – простое число. Доказать, что:

a) если k не делится на p, то 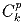делится на p;

b) (a + b) p ≡ a p + b p (mod %)%p;

c) (a + b + … + d) p ≡ a p + b p + … + d p (mod %)%p.

d) Вывести из пункта c) малую теорему Ферма: a p ≡ a (mod %)%p.

Задача 29: На окружности отмечено 11 точек.

a) Сколько существует многоугольников с вершинами в отмеченных точках?

b) Каких из них больше: содержащих данную отмеченную точку или остальных?

Решение: а)

Задача 30: Сколько способов выбрать:

a) 3 пары из 100 человек?

b) n пар из 2n человек?

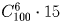
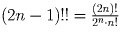
Решение: а) ; b) .

Задача 31: Каких 6-значных чисел больше: представляющихся в виде произведения двух трехзначных или остальных?

Решение: Остальных

Задача 32: На дороге длиной 999 километров стоят 1000 километровых столбов, на каждом из которых написаны два числа – расстояние до начала и до конца дороги. Сколько среди этих столбов таких, на которых числа записаны только двумя различными цифрами?

Источник

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Источник