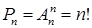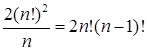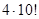Сколько способов сесть за круглый стол

Этикет. Круглый стол

Если есть сомнения, какой стол поставить в гостиной или заказать в ресторане – выбирайте круглый, не ошибетесь. Обед или ужин за таким столом – это очень романтично.

А теперь, обо всем по порядку

Многие из нас о круглых столах узнали из книг о короле Артуре. Рыцари собирались за круглым столом, чтобы показать, что все равны.

Так что, если вы собираетесь дружной компанией, то круглый стол – это то, что вам надо: все видят глаза друг друга, нет острых углов, которые разъединяют. Впрочем, и малознакомые люди за круглым столом быстрее сближаются.

Но и за круглыми столами правила этикета диктуют определенные каноны рассадки.

Кто где садится

Хотя у круглого стола нет ни начала ни конца, все же есть “главное место” – напротив входа.

Главный гость или хозяин и его супруга садятся по разные стороны круглого стола. Исключение – только молодожены на свадьбе.

По правую руку от хозяина садится самая уважаемая женщина, по правую руку от хозяйки – самый уважаемый мужчина.

Мужчин и женщин стараемся чередовать. Об основных правилах рассадки гостей я уже писал, так что не буду повторяться, впереди еще много интересного и удивительного.

Стоит отметить, что в жизни всегда бывают исключения.

Если в ресторане вы занимаете несколько круглых столов, например, на свадьбу или юбилей, то это целое искусство – правильно рассадить гостей. Надо избегать за одним столом сослуживцев, бывших супругов, разновозрастных гостей. И не дай Бог, если за одним столом окажутся два шутника-балагура: весь вечер они будут соревноваться между собой. В то же время, надо рассадить гостей так, чтобы им не было скучно друг с другом – учитывайте их интересы.

Но крупные торжества – это тема для отдельной заметки, а сейчас о небольших домашних застольях.

Маленький стол

Самый минимальный вариант – стол на двоих, скорее всего, это будет кофейный столик. В идеале – они сидят друг напротив друга. Если в уличном кафе, – то можно сесть рядом, чтобы обозревать проходящих по улице людей.

Помимо семейной трапезы, или романтического свидания, столик на двоих уместен и в большой компании. Если вы хотите пообщаться с человеком, то можете присесть с ним за небольшой столик, которые обычно стоят в больших ресторанах или холлах отелей.

Если хозяин большого кабинета с большим Т-образным столом пригласил вас за маленький столик выпить чашку чая или кофе, то тем самым, он оказал вам большое уважение. Ваш вопрос, скорее всего, будет решен положительно, или от вас чего-то хотят.

Стол на четверых

Пожалуй, самый простой вариант рассадки.

Хозяева друг напротив друга, а пришедшая к ним семейная пара напротив друг друга, по правую руку от хозяина гостя, по правую руку от хозяйки – гость.

Думаю, что принцип понятен и рисовать схему на большее число гостей не надо.

Тем более, что число приглашенных может быть нечетным, и если вдруг рядом окажутся мужчины или женщины – ничего страшного, жизнь многообразна и на каждую ситуацию правил не напасешься.

Размеры

Понятно, что в ресторане метродотель предложит стол, исходя из того, какие есть свободные, и сколько человек пришло с вами.

Но приемы мы устраиваем и дома, так что немного математики, прежде чем отправиться в мебельный магазин за новым столом.

Существуют стандарты, сколько надо места на столе для одного человека. От 55 до 70 сантиметров. Исходя из этого, можно подсчитать размеры круглого стола.

На сколько гостей, какой размер

Если вы ведете уединенный образ жизни, то рассчитываете стол семья + 2 человека.

Если гости у вас бывают время от времени – семья + 4.

Если дверь не закрывается… считайте сами, исходите из того, что одновременно за стол сядет 10 человек.

А теперь берем в руки калькулятор и вспоминаем математику средней школы.

D – Диаметр стола

L – Длина окружности ( 55 см на человека умноженные на число людей).

π – Постоянная величина, округлённо равная 3.14

Если лень считать, то вот шпаргалка

• Минимальный размер — 60 см для 2 человек:
• 110 см –4;
• 130 см – 6;
• 150 см – 8;
• 170 см – 10.

Но если постараться, то за стол 170-180 см можно усадить 12, а то и 14 гостей.

Круглые столы диаметром более 180 см крайне неудобны: слишком большим получается расстояние от сидящих напротив, а также от общих блюд, расположенных в центре стола.

Поэтому в ресторанах обычно центр стола украшают цветами, или ставят вращающийся столик.

Не будем забывать, что многие круглые столы «легким движением руки» становятся овальными.

Размеры комнаты

Круглый стол, чаще всего, ставят посередине гостиной, и здесь есть свои расчеты, какие расстояния до стен или предметов должны быть.

Если вы ставите круглый стол в центре комнаты только на время приема, то расстояние от стола до стены или предметов мебели должно быть не менее 90 см, если стол стоит в комнате постоянно – больше метра.

Так что, если у вас стол 150 см, то минимальная площадь помещения должна быть 8 метров, а если шкафы или стеллажи, то еще больше, место большого круглого стола явно в гостиной.

Компактность

А теперь самое интересное и парадоксальное.

Круглые столы на одинаковое число гостей компактнее, чем прямоугольные или квадратные.

Дабы не утомлять вас расчетами, вот три картинки:

Прямоугольный стол – самый «громоздкий» вариант.

Резюме

Если позволяет площадь комнаты, выбирайте круглый стол – это так по-семейному!

Источник

Рассадка гостей

Добрый вечер! У меня есть задача:

Несколько человек садятся за круглый стол. Будем считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях. Сколькими различными способами можно посадить четырех человек? А семь человек? Во скольких случаях два данных человека из семи оказываются соседями? Во скольких случаях данный человек (из семи) имеет двух данных соседей?

Мой вариант решения для 4-х гостей: 4*3*2*1 Это же неправильно? Расскажите пожалуйста как это делать? Спасибо!

Добавлено через 16 часов 37 минут
Никто не подскажет?((

Перебор вариантов приглашения гостей на день рождения
Добрый день Прошу помочь в решении. День бьюсь, не могу понять пока решения. Задача следующая.

Распределение (рассадка) сотрудников по рабочим местам
Приветствую всех гением, спасите мой мозг! Не давно столкнулся с такой проблемой: Есть excel файл с.

Задача про гостей
Задача: представьте, что вы намерены пригласить к себе шестерых гостей, но за вашим столом могут.

Скрипт IP гостей сайта
Подскажите что в index.php дописать что бы в текстовый документ записывались ip гостей сайта и.

Решение

гостей всего — m
соседей у одного гостя — n (всегда равно 2)
разных пар двух соседей для одного гостя — число сочетаний из (m — 1) по n

и для n = 2 окончательно

решения:
для 4-х гостей:

в формуле не учитывается «сторона соседства» — «слева Маша, справа Даша» и «слева Даша, справа Маша» считаются одним вариантом.
очевидно, что количество способов рассадки при учёте «сторон соседства» будет вдвое большим.

kristi1, Возьмем рассадку A. В нее приходит человек и создает n новых рассадок, пусть это будет множество R_A. Все они разные с точки зрения соседства.
Теперь возьмем другую рассадку B (она отличается от A). Снова приходит этот тип и создает множество R_B. Но не факт, что множества R_A и R_B не пересекаются, т.е. что нет одинаковых с точки зрения соседства. Т.е. я просто не знаю, как это доказывать.
Плюс, мои результаты не совпадают с результатами Notortep, что наводит на мысль, что скорее всего я ошибаюсь

Добавлено через 43 минуты
Чтобы проверить свои предположения, обратился к эксперементу. Написал программку перебора.
Вот результат
F(3) = 1
F(4) = 3
F(5) = 12
F(6) = 60
F(7) = 360
F(8) = 2520
Выходит, моя формула правильная!
Правда и программа может содержать ошибки, но она такая простенькая!
Плюс совпадение для n=3, n=4 утешают.

Добавлено через 4 минуты
Кажется, можно доказать, что если какие-то рассадки из R_A и R_B совпадают, то совпадают и A с B

Источник

Сколько способов сесть за круглый стол

В школьном курсе понятие «круговые перестановки» встречается в 7 классе в учебнике по алгебре в разделе «Для тех, кому интересно» [3].

В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить в ряд, или, как говорят математики, упорядочить, все элементы некоторого множества.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Получаемые при этом упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них элементов, называют перестановками без повторений из п элементовили «круговыми перестановками».

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют “сочетания”. В ХII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из п слогов. Как научная дисциплина, комбинаторика сформировалась в Х V II в. В книге “Теория и практика арифметики” (1656 г.) французский автор Андре Таке также посвящает сочетаниям и перестановкам целую главу.

Б. Паскаль в “Трактате об арифметическом треугольнике” и в “Трактате о числовых порядках” (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин “комбинаторика” стал употребляться после опубликования Лейбницем в 1665 г. работы “Рассуждение о комбинаторном искусстве”, в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги “Аг s соп j ес t ап d i” (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в ХIХ в [4].

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения. При решении задач на перестановки используется правило умножения.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Рассмотрим задачу: В турнире четверо участников. Сколькими способами могут быть распределены места между ними?

Будем рассуждать в соответствии с правилом умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье любой из двух оставшихся, а на четвертом месте останется последний участник. Значит, места между участниками могут быть распределены 4 ۰ 3 ۰ 2 ۰ 1 = 24 способами. Решив задачу, мы фактически подсчитали число перестановок для множества из четырех элементов. Рассуждая точно так же, можно показать, что для множества из пяти элементов число перестановок равно 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1, а для множества из десяти элементов это число равно 10 ۰ 9 ۰ 8 ۰ 7 ۰ б ۰ 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1.

Вообще если множество содержит п элементов, то число перестановок равно произведению п(п – 1)(п – 2) ۰…۰ 2 ۰ 1. Множители в этом произведении можно записать в обратном порядке: 1 ۰ 2 ۰ . ۰ (п – 2)(п – 1)п.

Такие произведения бывают очень длинными и часто выражаются огромными числами. Однако в математике есть специальный символ для их обозначения. Произведение всех натуральных чисел от 1 до п обозначают п! (читают: «п факториал»). Значение выражения п! можно найти для любого натурального числа п (при этом считают, что 1! = 1).

Факториалы растут удивительно быстро. Можно понаблюдать за их изменением, рассмотрев таблицу, в которой приведены факториалы чисел от 1 до 10:

Источник

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .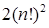

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .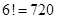

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .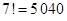

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .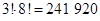

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .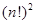

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .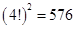

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .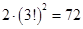

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник