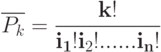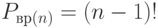Сколько способов расставить по кругу

Сколькими способами можно расставить предметы по кругу?

Сколькими способами можно рассадить 6 человек за столом по кругу
Добрый день. Есть задача: Сколькими способами можно рассадить 6 человек за столом: а) в ряд; б) по.

Сколькими способами можно расставить книги?
На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и.

Сколькими способами можно расставить конфеты?
Всем привет! Есть одна сложная задача на комбинаторику: Имеются конфеты трех типов.

Сколькими способами можно расставить спортсменов?
Из группы в 12 человек выбирают 4-х участников эстафеты 800*400*200*100.Сколькими способами можно.

Можно поподробнее, пожалуйста. Пример хотя бы одного класса.

Добавлено через 27 секунд
Я понял, что речь идёт про классы еквивалентности, но не могу себе это представить.

Решение

Сколькими способами можно расставить книги?
Помогите решить пожалуйста вот такую задачу На полку нужно установить 17 разных книг, из которых.

Сколькими способами можно расставить 8 спортсменов
Доброй ночи! Задание: Сколькими способами можно расставить 8 спортсменов на 3 одинаковых дорожках.

Сколькими способами можно расставить фишки на доске?
Сколькими способами можно расставить на доску с 16 квадратов а) 16 различных фишек, так чтобы.

Сколькими способами можно расставить учебные тревоги
Вы разрабатываете учебное расписание для военной части. Известно, что в месяце 30 дней, и в.

Источник

Круговые перстановки

Цель данной работы — рассмотреть круговые перестановки как один из способов решения комбинаторных задач на расположение элементов множества в определённом порядке. Использование данного способа позволяет решать некоторые задачи нетрадиционным методом, а иногда и упрощают их решение. В последние годы необычайно возросла роль комбинаторных методов не только в самой математике, но и в ее многочисленных приложениях: в физике, химии, биологии, лингвистике, технике, экономике. Расчет вероятностей во многих случаях приводит к комбинаторным задачам. Кроме того задачи, решаемые с использованием комбинаторных методов и комбинаторных подходов встречаются в качестве занимательных или встречаются в олимпиадных заданиях, поэтому работа имеет практическую и познавательную направленность.

Скачать:

Вложение	Размер
krugovye_perestanovki.docx	496.29 КБ

Предварительный просмотр:

XV республиканский научный конкурс молодых исследователей

«Шаг в будущее Осетии»

Автор: Восканян Армен

МБОУ «СОШ № 2 ст. Архонская», 7 «А» класс

Уймина Татьяна Алексеевна,

учитель математики МБОУ «СОШ № 2 ст. Архонская»

Россия, РСО – Алания, ст. Архонская

МБОУ «СОШ № 2 ст. Архонская», 7 «А» класс

Цель данной работы — рассмотреть круговые перестановки как один из способов решения комбинаторных задач на расположение элементов множества в определённом порядке. Использование данного способа позволяет решать некоторые задачи нетрадиционным методом, а иногда и упрощают их решение. В последние годы необычайно возросла роль комбинаторных методов не только в самой математике, но и в ее многочисленных приложениях: в физике, химии, биологии, лингвистике, технике, экономике. Расчет вероятностей во многих случаях приводит к комбинаторным задачам. Кроме того задачи, решаемые с использованием комбинаторных методов и комбинаторных подходов встречаются в качестве занимательных или встречаются в олимпиадных заданиях, поэтому работа имеет практическую и познавательную направленность.

Россия, РСО – Алания, ст. Архонская

МБОУ «СОШ № 2 ст. Архонская», 7 «А» класс

В последние годы необычайно возросла роль комбинаторных методов не только в самой математике, но и в ее многочисленных приложениях: в физике, химии, биологии, лингвистике, технике, экономике. Расчет вероятностей или решение задач на упорядочение элементов некоторого множества во многих случаях приводит к комбинаторным задачам. Кроме того задачи, решаемые с использованием комбинаторных методов и комбинаторных подходов встречаются в качестве занимательных или встречаются в олимпиадных заданиях, поэтому работа имеет практическую и познавательную направленность.

Рассматриваемый метод круговых перестановок является одним из способов решения комбинаторных задач на расположение элементов множества в определённом порядке. Использование данного способа позволяет решать некоторые задачи нетрадиционным методом, а иногда и упрощают их решение, обогащает арсенал средств, используемых при их решении .

Рассмотрение элементов комбинаторики несёт большую образовательную задачу, способствует развитию «комбинаторного» мышления, расширению математического кругозора, облегчает усвоение в дальнейшем элементов теории вероятностей. Для этого в работе используется краткий исторический материал и хорошо знакомый пример из литературы.

Выполнение данной работы вызвано интересом к математике и желанием приобрести первоначальные навыки в решении комбинаторных задач.

В школьном курсе понятие «круговые перестановки» встречается в 7 классе в учебнике по алгебре в разделе «Для тех, кому интересно» [ 3 ].

В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить в ряд, или, как говорят математики, упорядочить, все элементы некоторого множества.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Получаемые при этом упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них элементов, называют перестановками без повторений из п элементов или «круговыми перестановками».

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют “сочетания”. В ХII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из п слогов. Как научная дисциплина, комбинаторика сформировалась в ХVII в. В книге “Теория и практика арифметики” (1656 г.) французский автор Андре Таке также посвящает сочетаниям и перестановкам целую главу.

Б. Паскаль в “Трактате об арифметическом треугольнике” и в “Трактате о числовых порядках” (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин “комбинаторика” стал употребляться после опубликования Лейбницем в 1665 г. работы “Рассуждение о комбинаторном искусстве”, в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги “Агs сопjесtапdi” (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в ХIХ в [4].

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения. При решении задач на перестановки используется правило умножения.

Каждое расположение элементов множества в определенном порядке называют перестановкой . Рассмотрим задачу: В турнире четверо участников. Сколькими способами могут быть распределены места между ними?

Будем рассуждать в соответствии с правилом умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье любой из двух оставшихся, а на четвертом месте останется последний участник. Значит, места между участниками могут быть распределены 4۰3۰2۰1 = 24 способами. Решив задачу, мы фактически подсчитали число перестановок для множества из четырех элементов. Рассуждая точно так же, можно показать, что для множества из пяти элементов число перестановок равно 5۰4۰3۰2۰1, а для множества из десяти элементов это число равно 10۰9۰8۰7۰б۰5۰4۰3۰2۰1.

Вообще если множество содержит п элементов, то число перестановок равно произведению п ( п – 1)( п – 2)۰…۰2۰1. Множители в этом произведении можно записать в обратном порядке: 1۰2۰. ۰( п – 2)( п – 1) п .

Такие произведения бывают очень длинными и часто выражаются огромными числами. Однако в математике есть специальный символ для их обозначения. Произведение всех натуральных чисел от 1 до п обозначают п! (читают: «п факториал»). Значение выражения п! можно найти для любого натурального числа п (при этом считают, что 1! = 1).

Факториалы растут удивительно быстро. Можно понаблюдать за их изменением, рассмотрев таблицу, в которой приведены факториалы чисел от 1 до 10:

Источник

Сколько способов расставить по кругу

В школьном курсе понятие «круговые перестановки» встречается в 7 классе в учебнике по алгебре в разделе «Для тех, кому интересно» [3].

В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить в ряд, или, как говорят математики, упорядочить, все элементы некоторого множества.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Получаемые при этом упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них элементов, называют перестановками без повторений из п элементовили «круговыми перестановками».

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют “сочетания”. В ХII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из п слогов. Как научная дисциплина, комбинаторика сформировалась в Х V II в. В книге “Теория и практика арифметики” (1656 г.) французский автор Андре Таке также посвящает сочетаниям и перестановкам целую главу.

Б. Паскаль в “Трактате об арифметическом треугольнике” и в “Трактате о числовых порядках” (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин “комбинаторика” стал употребляться после опубликования Лейбницем в 1665 г. работы “Рассуждение о комбинаторном искусстве”, в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги “Аг s соп j ес t ап d i” (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в ХIХ в [4].

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения. При решении задач на перестановки используется правило умножения.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Рассмотрим задачу: В турнире четверо участников. Сколькими способами могут быть распределены места между ними?

Будем рассуждать в соответствии с правилом умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье любой из двух оставшихся, а на четвертом месте останется последний участник. Значит, места между участниками могут быть распределены 4 ۰ 3 ۰ 2 ۰ 1 = 24 способами. Решив задачу, мы фактически подсчитали число перестановок для множества из четырех элементов. Рассуждая точно так же, можно показать, что для множества из пяти элементов число перестановок равно 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1, а для множества из десяти элементов это число равно 10 ۰ 9 ۰ 8 ۰ 7 ۰ б ۰ 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1.

Вообще если множество содержит п элементов, то число перестановок равно произведению п(п – 1)(п – 2) ۰…۰ 2 ۰ 1. Множители в этом произведении можно записать в обратном порядке: 1 ۰ 2 ۰ . ۰ (п – 2)(п – 1)п.

Такие произведения бывают очень длинными и часто выражаются огромными числами. Однако в математике есть специальный символ для их обозначения. Произведение всех натуральных чисел от 1 до п обозначают п! (читают: «п факториал»). Значение выражения п! можно найти для любого натурального числа п (при этом считают, что 1! = 1).

Факториалы растут удивительно быстро. Можно понаблюдать за их изменением, рассмотрев таблицу, в которой приведены факториалы чисел от 1 до 10:

Источник

Комбинаторика

Комбинаторика — один из разделов дискретной математики, который приобрел важное значение в связи с использованием его в ВТ, кибернетике, робототехнике . Большинство задач комбинаторики можно сформулировать как задачи теории конечных множеств, поэтому эти две темы — элементы теории множеств и комбинаторика — рассматриваются взаимосвязано.

Человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Например, сколькими способами могли быть распределены золотая, серебряная и бронзовая медали на Олимпийских играх в Сеуле по баскетболу; или сколькими различными способами можно разместить здания на площади ? Задачи такого типа называются комбинаторными .

С комбинаторными вычислениями приходится иметь дело представителям многих специальностей: ученому-химику при рассмотрении различных возможных типов связи атомов в молекулах, биологу — при изучении возможных последовательностей чередования аминокислот в белковых соединениях, диспетчеру — при составлении графика движения и т. д.

Комбинаторика возникла в XVI веке. В то время в жизни привилегированных слоев общества большое место занимали азартные игры (карты, кости). Были широко распространены лотереи. Возникали вопросы: сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей? Эти и другие проблемы оказались движущей силой в развитии комбинаторики .

Теоретические исследования вопросов комбинаторики предприняли Паскаль и Ферма, Бернулли, Лейбниц и Эйлер и др.

Для инженерных специальностей университета комбинаторные задачи приходится решать в следующих случаях:

1. при конструировании :
   • для оптимального размещения элементов системы;
   • для размещения микросхем на плате или элементов на кристалле;
   • при трассировке (выборе маршрута);

Общие правила комбинаторики

Рассмотрим некоторые конкретные задачи.

Задача. 1. «Суеверные велосипедисты»

«Опять восьмерка» — воскликнул председатель клуба велосипедистов, — а все потому, что у меня билет № 008. Надо менять номера и проводить перерегистрацию».

Итак, сколько членов было в клубе, если известно, что использованы все трехзначные номера, не содержащие ни одной цифры 8?

00	01	02	.	09
10	11	12	.	19
20	21	22	.	29
30	31	32	.	39
40	.	.	.	.
50	.	.	.	.
60	.	.	.	.
70	.	.	.	.
80	.	.	.	.
90	.	.	.	.

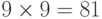
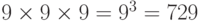
Для решения этой задачи определим сначала, сколько однозначных номеров не содержит цифру 8? Это 0, 1, 2, 3, 4, 5, 6, 7, 9 — всего девять цифр, а теперь найдем все двузначные номера: их ( таблица ). За каждым двузначным номером можно поставить любую допустимую цифру, следовательно, . Значит в клубе было 729 велосипедистов.

В другом клубе велосипедисты были ещё суевернее и решили, что цифра 0 тоже похоже на вытянутое колесо и они отказались от этой цифры .

Сколько членов было в клубе, если номера билетов были трехзначными и не включали цифр 0 и 8? .

Задача 2. «Секретный замок»

В сейфах применяют секретные замки, которые открываются, когда набран шифр . Этот шифр набирают с помощью одного или нескольких дисков. Пусть на диск нанесены 12 букв, а секретное слово- шифр состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим шифра?

Всего попыток , одна из которых удачная, следовательно неудачных попыток .

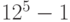
Задача 3. » Команда космического корабля»

В случае, когда число возможных выборов на каждом шаге зависит от того какие элементы были выбраны ранее, удобно решение изображать в виде «дерева». Сначала из одной точки проводят столько отрезков, сколько различных выборов можно сделать на 1-м шаге. Из конца каждого отрезка проводят столько отрезков, сколько можно сделать на 2-м шаге и т. д. В результате получается » дерево решений «.

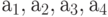
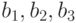
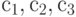
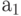
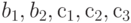
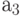
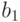
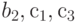
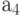
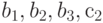
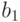
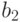
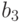
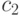
Рассмотрим задачу о формировании команды космического корабля. Известно, что возникнет вопрос психологической совместимости. Предположим, надо составить команду из 3-х человек: командира, инженера и врача. На место командира есть четыре кандидата: , на место инженера три — , на место врача три — . Проведенная проверка показала, что совместим с ; совместим с ; совместим с и ; совместим с ; не совместим с ; не совместим с ; не совместим с .

Сколькими способами при этих условиях может быть составлена команда корабля? По результатам совместимости строится дерево решений ( рис. 5.1). Итак, всего 11 комбинаций, а без ограничения .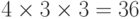

Упорядоченные множества. Перестановки

Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от до где — число элементов множества .

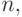
Всякое конечное множество можно сделать упорядоченным, если, например, переписать все элементы множества в некоторый список ( 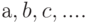.), а затем каждому элементу присвоить номер.

Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком.

Различные упорядоченные множества , которые отличаются лишь порядком элементов, называются перестановками этого множества .

Пример. Перестановки множества 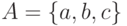из 3-х элементов имеют вид .

Число перестановок из элементов !

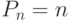
Задача 1. Сколькими способами можно разместить на плате 4 элемента? .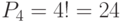

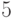
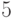
Задача 2. Сколькими способами можно выстроить в линейку 10 человек (5 девушек и 5 юношей) с условием, чтобы девушки и юноши чередовались, первая — девушка? 5 девушек можно разместить ! способами, а 5 юношей аналогично !. Следовательно, всего способов .

Перестановка с повторением

Если рассматривать упорядоченные -элементные наборы из множества , которые состоят не только из различных элементов множества , но содержат некоторые повторяющиеся элементы, то получим перестановки с повторением.

Пусть — множество из элементов и — натуральные числа , такие, что их сумма равна , а n» style=»display: inline; «>.

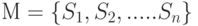
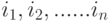
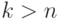
Каждый упорядоченный набор элементов содержащий элемент ровно раз ( ) называется перестановками множества с повторением:

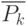
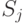
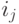
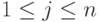
Примечание: при 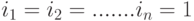получим перестановки множества из элементов без повторений.

Пример. Сколько различных шестизначных чисел можно составить из цифр 1, 1, 1, 5, 5, 9? Подставим в формулу различных шестизначных чисел.

Задача 2. Сколько различных слов можно получить, переставляя буквы слова «математика»?

Перестановки предметов, расположенных в круг

Задача 1. «Хоровод». Семь девушек водят хоровод. Сколькими различными способами они могут встать в круг (рис. 5.2,а)?

Если бы они стояли на месте, то количество способов — 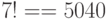. Но так как танцующие кружатся, то их положение относительно окружающих не имеет роли, следовательно, важно лишь взаимное расположение. Поэтому перестановки , переходящие друг в друга, надо считать одинаковыми. Но из каждой перестановки можно получить еще 6 путем вращения — 7 мест: различных перестановок девушек в хороводе.

В общем случае, если рассматривать предметов, расположенных в круг, и считать одинаковыми расположения, переходящие друг в друга при вращении, то число различных перестановок равно

Задача 2. Сколько ожерелий можно составить из 7 бусинок?

По аналогии с предыдущей задачей можно подумать, что 720. Но ожерелье можно не только вращать, но и перевернуть (рис. 5.2,б). Поэтому ответ 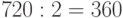, т. е.

Источник