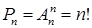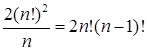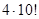Сколько способов круглый стол мужчин женщин

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .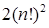

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .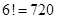

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .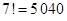

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .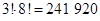

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .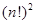

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .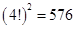

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .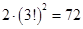

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?

Здравствуйте, уважаемые. Я к вам снова по поводу комбинаторики. Есть задача:
Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом? А если они садятся не за круглый стол, а на карусель (способы, переходящие друг в друга при вращении карусели, считаются совпадающими) ?

Первая часть задачи решается как n!*n!, а как решить про карусель, я не поняла? Спасибо большое!

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, не подскажите как сделать подобную задачу если надо рассадить на карусель 6 детей и 3.

Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две женщины не сидели рядом?
Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две.

Сколькими способами можно посадить n мужчин и n женщин за круглый стол с определенным условием?
Сколькими способами можно посадить n мужчин и n женщин за круглый стол так, чтобы никакие два лица.

Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12 мужчин и 20 женщин?
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12.

kristi1, разделите на 2n

Добавлено через 3 минуты
Кстати, первая часть — 2*n!*n!, т.к. на стул номер 1 можно посадить как мужчину, так и женщину

Решение

стол от карусели отличается тем, что стулья за столом пронумерованы: есть стул №1, стул №2. стул №10
на карусели нумерация отсутствует

за столом
сначала, как и положено, усаживаем женщин так, чтобы между ними были пустые места
это можно сделать 5! = 120 способами (число перестановок)
однако усадить женщин можно как начиная со стула №1 (по нечётным местам), так и со стула №2 (по чётным местам)
следовательно, 5 женщин можно рассадить 2 * 120 = 240 способами

на оставшиеся 5 мест сядут мужчины — 5! = 120 способами

в итоге за стол мужчин и женщин можно посадить 240 * 120 = 28 800 способами
или в общем виде для n пар мужчин и женщин за столом — 2*n!*n!

на карусели нет нумерации, следовательно, коэффициент 2, введёный при рассадке женщин, не нужен
ответ для карусели — 14 400 способов
в общем виде для n пар мужчин и женщин на карусели — n! * n!

в решении выше ошибка — умножается на 2 (для стола) правильно, а делится (для карусели) почему-то на 2n, что неправильно

Источник

Комбинаторная задача. Способы рассадить людей за столом.

Сколькими способами можно рассадить гостей за столом
Здравствуйте еще раз. Неделю назад писал олимпиаду по программированию. И попалась такая задачка.

Сколькими способами можно рассадить 6 человек за столом по кругу
Добрый день. Есть задача: Сколькими способами можно рассадить 6 человек за столом: а) в ряд; б) по.

Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин
Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин так, чтобы мужчины не.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Решение

А какая разница: круг или ряд? Есть n мужчин и n женщин. Есть круглый стол с 2*n местами. Мы их (места) нумеруем. На парные места, например, садим мужчин.
Тогда, на 2-е место можно посадить одного из n мужчин, на 4-е — одного из n-1 мужчин, на 6-е — одного из n-2 мужчин, . на (2n-2)-е — одного из 2 мужчин, на 2n-е — последнего что останется.
Всего n*(n-1)*(n-2)*. *2*1=n!
Аналогично, для непарных мест и для женщин. Тоже n! способов.
Потом можно еще садить мужчин на непарные, а женщин на парные.
Всего 2*n!*n! способов.

Или я что-то не так понял в условии задачи?

Добавлено через 1 час 51 минуту
Понял. Имеется ввиду, что разные «рассадки» будут тогда, когда хотя бы у одного человека хотя бы один из соседей отличается. Тогда в случае, когда все пересядут на одно место вправо, будет та же «рассадка».
Тогда 2*n!*n!/n=2*n!*(n-1)!

Есть 10 людей ,где 1 жених ,1 невеста ,нужно рассадить 6 людей в ряд так , чтобы среди них были жених и невеста
сколько комбинаций ? я думал что ответ 1*1*7*6*5*4, но говорят ответ другой .

Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.

Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.

Поиск количества способов рассадить людей разных национальностей
Задача 4. Сколькими способами можно посадить рядом 3 англичан, 3 французов и 3 немцев так, чтобы.

Определить количество сочетания людей за круглым столом
За столом сидят n кол-во магов(n — всегда четное). Вместе они выбирают себе по паре и одновременно.

Найти способы рассадить заданное количество флегматичных и меланхоличных ленивцев по вольерам
Выставка большое событие в жизни любого ленивца. При этом ленивцы не могут перебороть свою природу.

Источник

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом? — Комбинаторика — Ответ 3435117

Ответ

стол от карусели отличается тем, что стулья за столом пронумерованы: есть стул №1, стул №2. стул №10
на карусели нумерация отсутствует

за столом
сначала, как и положено, усаживаем женщин так, чтобы между ними были пустые места
это можно сделать 5! = 120 способами (число перестановок)
однако усадить женщин можно как начиная со стула №1 (по нечётным местам), так и со стула №2 (по чётным местам)
следовательно, 5 женщин можно рассадить 2 * 120 = 240 способами

на оставшиеся 5 мест сядут мужчины — 5! = 120 способами

в итоге за стол мужчин и женщин можно посадить 240 * 120 = 28 800 способами
или в общем виде для n пар мужчин и женщин за столом — 2*n!*n!

на карусели нет нумерации, следовательно, коэффициент 2, введёный при рассадке женщин, не нужен
ответ для карусели — 14 400 способов
в общем виде для n пар мужчин и женщин на карусели — n! * n!

в решении выше ошибка — умножается на 2 (для стола) правильно, а делится (для карусели) почему-то на 2n, что неправильно

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, не подскажите как сделать подобную задачу если надо рассадить на карусель 6 детей и 3.

Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две женщины не сидели рядом?
Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две.

Сколькими способами можно посадить n мужчин и n женщин за круглый стол с определенным условием?
Сколькими способами можно посадить n мужчин и n женщин за круглый стол так, чтобы никакие два лица.

Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12 мужчин и 20 женщин?
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12.

Сколькими способами можно рассадить этих людей, чтобы знакомые сидели рядом?
Помогите пожалуйста с задачами. Для закрытия всех долгов не хватает только этого 1. Среди 12.

Сколькими способами можно выбрать 4 женщин и 3 мужчин?
Сколькими способами можно выбрать 4 женщин и 3 мужчин из 9 женщин и 6 мужчин, если не могут быть.

Сколькими способами можно составить компанию из 6 мужчин и 6 женщин?
3)У мужа 12 знакомых, среди которых 5 женщин и 7 мужчин, а у жены 7 женщин и 5 мужчин. Сколькими.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Источник

Комбинаторика сколькими способами можно посадить за круглый стол

Как решать, находил эти две задачи раздельно, но не понимаю как поменяется количество комбинаций.

Сколькими способами можно посадить за круглый стол 6 мужчин и 6 женщин так, чтобы никакие два лица одного пола не сидели рядом? Считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях.

задан 21 Мар 18:36

ну, нашли число вариантов рассадки мужчин (через одного). потом на свободные места рассадили женщин.

что вызвало трудности.

@all_exist Написал ведь, вот это условие «Считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях.» Не понятно как из-за него меняется количество способов. Так чтоли(n-1)! * n!? = 6!*7!=3 628 800?

@bronzor: да, при таком соглашении будет (n-1)!n!.

@falcao и это ответ? Условие после вопросительного знака про игнорируется?

@bronzor: оно не игнорируется. Представьте себе, что места пронумерованы, и рассадки считаются разными, если кто-то сел на место с другим номером. Тогда ответ будет n!n!. А здесь при поворотах рассадки получаются те же, и выходит (n-1)!n!. Правда, если подходить формально, то при отражениях соседи остаются теми же, и тогда число в ответе надо разделить ещё на 2. Другое дело, что это несколько противоестественная трактовка. Точнее было бы считать, что рассадка та же, если мой сосед слева остался тем же, и то же для соседа справа. Видимо, это и имелось в виду, но мысль не так передали.

Источник