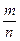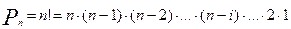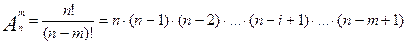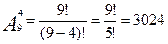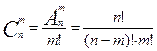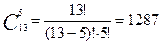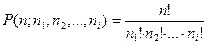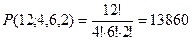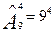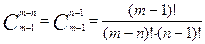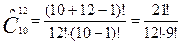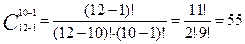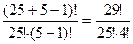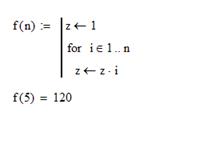Сколько способов чтобы рассадить 12 человек за круглым столом

Комбинаторная задача. Способы рассадить людей за столом.

Сколькими способами можно рассадить гостей за столом
Здравствуйте еще раз. Неделю назад писал олимпиаду по программированию. И попалась такая задачка.

Сколькими способами можно рассадить 6 человек за столом по кругу
Добрый день. Есть задача: Сколькими способами можно рассадить 6 человек за столом: а) в ряд; б) по.

Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин
Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин так, чтобы мужчины не.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Решение

А какая разница: круг или ряд? Есть n мужчин и n женщин. Есть круглый стол с 2*n местами. Мы их (места) нумеруем. На парные места, например, садим мужчин.
Тогда, на 2-е место можно посадить одного из n мужчин, на 4-е — одного из n-1 мужчин, на 6-е — одного из n-2 мужчин, . на (2n-2)-е — одного из 2 мужчин, на 2n-е — последнего что останется.
Всего n*(n-1)*(n-2)*. *2*1=n!
Аналогично, для непарных мест и для женщин. Тоже n! способов.
Потом можно еще садить мужчин на непарные, а женщин на парные.
Всего 2*n!*n! способов.

Или я что-то не так понял в условии задачи?

Добавлено через 1 час 51 минуту
Понял. Имеется ввиду, что разные «рассадки» будут тогда, когда хотя бы у одного человека хотя бы один из соседей отличается. Тогда в случае, когда все пересядут на одно место вправо, будет та же «рассадка».
Тогда 2*n!*n!/n=2*n!*(n-1)!

Есть 10 людей ,где 1 жених ,1 невеста ,нужно рассадить 6 людей в ряд так , чтобы среди них были жених и невеста
сколько комбинаций ? я думал что ответ 1*1*7*6*5*4, но говорят ответ другой .

Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.

Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.

Поиск количества способов рассадить людей разных национальностей
Задача 4. Сколькими способами можно посадить рядом 3 англичан, 3 французов и 3 немцев так, чтобы.

Определить количество сочетания людей за круглым столом
За столом сидят n кол-во магов(n — всегда четное). Вместе они выбирают себе по паре и одновременно.

Найти способы рассадить заданное количество флегматичных и меланхоличных ленивцев по вольерам
Выставка большое событие в жизни любого ленивца. При этом ленивцы не могут перебороть свою природу.

Источник

Сколькими способами можно посадить за круглым столом 12 мужчин и 7 женщин?

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, уважаемые. Я к вам снова по поводу комбинаторики. Есть задача: Сколькими.

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, не подскажите как сделать подобную задачу если надо рассадить на карусель 6 детей и 3.

Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12 мужчин и 20 женщин?
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12.

Понятно, что все сидящие за столом различимы. А различимы ли места за столом?

Добавлено через 1 час 10 минут
Впрочем, вычислив, сколько способов рассадки существует при неразличимых местах за столом, и поделив полученный результат на по-моему, мы вычислим, сколько способов рассадки существует при различимых местах за столом.

Я предполагаю, что для решения задачи можно сначала вычислить, сколько способов рассадки существует для мужчин и женщин при том, что никакие две женщины не сидят рядом. Затем от полученного числа нужно отнять количество способов исключить пятерых лишних женщин.

Каково Ваше мнение насчёт предложенного мной?

Я пришёл к выводу, что моё предложение плохое. Наверное, задачу нужно свести к вычислению количества способов рассадить семерых женщин по двенадцати пустым местам, стоящим по одному между местами, которые заняты мужчинами.

Выбрать семь мест для женщин можно способами. Поместить на эти места женщин можно способами. Поместить мужчин на мест можно способами.

В результате, по-моему. тот же ответ, что и в предыдущем сообщении.

Добавлено через 11 минут
Наверное, нужно ещё учесть, что при различимых местах за столом выбрать мест для мужчин можно двумя способами.

Добавлено через 4 часа 31 минуту
damchke, интересно узнать, каковы Ваши соображения по решению задачи.

Источник

Теоретическая часть

Лабораторная работа №1. Случайные события

«Классическое определение вероятности. Основные формулы комбинаторики».

Теоретическая часть.

Классическая схема позволяет вычислять вероятности без проведения случайного эксперимента, основываясь лишь на свойстве симметрии возможных исходов испытания, так что нет оснований считать какой-либо из исходов более вероятным, чем другой.

Определение: Вероятностью случайного события А, называется отношение числа m исходов, благоприятствующих событию А, к числу всех равновозможных исходов испытания, составляющих полную группу несовместных событий.

Р(А)=

При непосредственном подсчете вероятностей часто используют формулы комбинаторики. Простейшими из них являются перестановки, сочетания, размещения и разбиения.

Перестановки отличаются друг от друга только порядком входящих в них элементов. Количество перестановок из n элементов:

Пример 1: Сколькими способами можно рассадить 10 человек за круглым столом, если имеет значение только порядок соседей.

Отметим, что вращение людей вокруг стола не меняет их взаимного расположения, поскольку соседи справа и слева остаются прежними. Если место за столом уникально, то существует 10! Способов рассадить людей за столом. Существует 10 вращений вокруг стола, поэтому делим на 10 и получаем 9! Способов рассадить людей за круглым столом, если значение имеет только порядок соседей.

Пусть М – множество, состоящее из n элементов.

Размещением из n элементов по m или упорядоченной (n,m)– выборкой, называется любой кортеж, состоящий из m, попарно различных элементов множества М.

Число размещений из n по m элементов:

Пример 2: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9, если все цифры различны.

Сочетанием из n элементов по m или неупорядоченной (n,m)­­– выборкой, называется любое подмножество множества M, состоящее из m элементов.

Надо заметить, что количество сочетаний отличается от числа размещений количеством перестановок каждого сочетания, то есть

Пример 3: Сколько существует вариантов выбора 5 карт трефовой масти из колоды, состоящей из 54 карт.

В колоде имеется 13 треф, из которых выбирается 5, поэтому

Пусть множество М разбито на k таких различных типов, что имеется n₁ неразличимых объектов типа 1, n₂ неразличимых объектов типа 2, и, вообще, n_i неразличимых объектов типа i (i=1,2,3,…,k), тогда количество различных размещений элементов множества:

Пример 4: Сколькими способами можно расставить на полке 12 книг, из которых 4 одинаковых учебника по математике, 6 одинаковых по информатике, 2 одинаковых по химии.

Если трактовать повторения как возвращения объекта во множество М и повторное его использование, то возникает идея размещений и сочетаний с повторениями. Их количество можно вычислить по формулам:

– количество размещений из n элементов по m с повторениями.

– количество сочетаний из n элементов по m с повторениями.

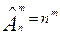
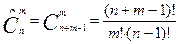
Пример 5: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9.

Так как нет ограничения на повторение цифр, то существует

Теорема: Если необходимо выбрать хотя бы по одному объекту из n по m с повторением, то количество различных сочетаний равно

Пример 6: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков.

Поскольку 12 пончиков выбираются из 10 видов с повторениями, то

Пример 7: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков, если необходимо выбрать хотя бы по одному пончику каждого вида .

Поскольку 12 пончиков выбираются из 10 видов с повторениями, то

Пример 8: Найдем количество различных решений уравнения

, где каждое слагаемое в левой части – неотрицательное число.

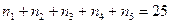
Это эквивалентно вопросу о том, сколько существует выборок вида

, где имеется объектов типа и

, но количество таких выборок — это количество различных сочетаний из 25 элементов по 5 элементов с повторениями. Итак, существуют

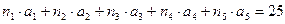
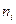
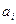
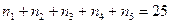
В среде MathCad нет встроенных функций для подсчета количества способов выбора объектов, поэтому необходимо воспользоваться возможностью программирования.

Чтобы создать программный модуль:

1. Введите выражение, которое будет находится слева от знака присваивания (имя функции);

2. Вызовите на экран панель Programming (программирование);

3. Нажмите на кнопку Add line[1] необходимое число раз;

4. В появившиеся местозаполнители введите необходимый программный код.

Для подсчета факториала необходимо организовать цикл. В среде MathCad это можно сделать с помощью оператора for и ранжирванной переменной, которая пробегает некоторое множество значений.

Фрагмент документа MathCad для подсчета факториала приведен ниже.

После того как программный модуль полностью определен и ни один из местозаполнителей ни остался пустым, функция может использоваться обычным образом.

Пример решения задачи на подсчет вероятности в среде МathCad:

Источник

Сколько способов чтобы рассадить 12 человек за круглым столом

За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Пусть первой за стол сядет девочка, рядом с ней есть два места, на каждое из которых может сесть 8 человек, из которых только одна девочка. Таким образом вероятность, что девочки будут сидеть рядом равна

Приведём другое решение (перестановки).

Число способов рассадить 9 человек по девяти стульям равно Благоприятным является случай, когда на «первом» стуле сидит «первая» девочка, на соседнем справа сидит «вторая» девочка, а на остальных семи стульях произвольным образом рассажены мальчики. Поскольку выбрать «первую» девочку можно двумя способами, количество таких исходов равно А так как «первым» стулом может быть любой из девяти стульев (стулья стоят по кругу), количество благоприятных исходов нужно умножить на 9. Таким образом, вероятность того, что обе девочки будут сидеть рядом, равна

Приведём другое решение (круговые перестановки).

Напомним, что число способов, которыми можно расположить n различных объектов по n расположенным по кругу местам равно (n − 1)! Поэтому посадить за круглым столом 9 детей можно 8! способами. Объединим двух девочек в пару, это можно сделать двумя способами; рассадить по кругу 7 мальчиков и эту неделимую пару можно 7! способами. Тем самым, посадить детей требуемым образом можно 2 · 7! способами, поэтому искомая вероятность равна

Рассуждая аналогично, получим, что в общем случае для n девочек и m мальчиков, сидящих девочки с девочками, а мальчики с мальчиками, количество способов занять места за круговым столом равно n!m!, а вероятность случайной рассадки требуемым образом равна

Источник