Практическое занятие на тему «Основные комбинаторные конфигурации»
Практическое занятие (2ч.)
Тема: Основные комбинаторные конфигурации .
научить применять комбинаторные конфигурации при решении задач;
сформировать умение находить нужную комбинаторную формулу при решении задачи;
формирование самостоятельности студента на занятии.
Математика / приложение к газете «Первое сентября», №15, 2004 г.
Стойлова Л.П. Математика.-М.: Изд. Центр Академия, 1997.
Прикладная комбинаторная математика.
Вариативная самостоятельная работа.
Повторение основных формул необходимых при решении комбинаторных задач.
Размещения с повторениями.
Задача 1. Сколько различных четырехзначных чи сел можно составить из цифр 2, 6, 7, 8 и 9, если каждая цифра может входить в комбинацию несколько раз?
Решение. Здесь порядок цифр существенен (2678 или 6278 — это разные числа). Поэтому имеем дело с кортежем длины 4 (четырехзначное число), каждый элемент которого можно выбрать пятью способами (цифр дано пять). Поэтому число различных комби наций равно 4 5 = 1024.
Задача 2. На референдуме предложены четыре вопроса, на которые надо ответить «да» или «нет». Сколько есть возможностей заполнения бюллетеня (на все вопросы надо дать ответ)?
Решение. Получаем кортеж длины 4 (столько во просов в бюллетене), каждый элемент может быть вы бран двумя способами («да» или «нет»). Поэтому число различных возможностей равно 2 4 =16.
Задача 3 . Неудовлетворенные решением Париса Гера, Афина и Афродита обратились к трем мудре цам с просьбой назвать прекраснейшую из них. Каж дый из мудрецов высказал свое мнение. Сколько мог ло возникнуть вариантов ответа на поставленный во прос у этой тройки?
Решение. Здесь вновь кортеж длиной 3 (три муд реца), каждый элемент которого может быть выбран шестью способами. Поэтому число различных возмож ностей равно 6 3 = 216.
Задача 4 . У Лены есть восемь красок. Она хочет написать ими слова «Новый Год». Сколькими спосо бами она может это сделать, если собирается каждую букву раскрашивать одним цветом?
Решение . Кортеж длиной 8 (восемь букв), каждый элемент может быть выбран восемью способами (во семь красок). Поэтому число способов равно 8 8 .
Задача 5. На железнодорожной станции имеется я семафоров. Сколько может быть дано различных сигналов при помощи этих семафоров, если каждый семафор имеет три состояния: горит либо зеленый, либо желтый, либо красный свет.
Решение. Имеем кортеж длины n (дано n семафо ров), каждый элемент которого можно выбрать тре мя способами (каждый семафор имеет три состояния). Поэтому различных сигналов можно дать 3 n .
Задачи для домашней работы
Сколько букв русского алфавита можно зако дировать, используя лишь комбинации точек и тире, содержащие только три знака?
Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать?
Задача 1. Из спортивного клуба, насчитывающего 30 членов, надо составить команду из четырех чело век для участия в эстафете на 100 + 200 + 400 + 800 (м). Сколькими способами это можно сделать?
Решение. Имеем кортежи длиной 4. Ни один элемент не может входить дважды (один бегун на один отрезок дистанции). Значит,
А 4 30 = 
Задача 2. Сколькими способами можно обозначить вершины данного треугольника, используя буквы А, В, С, D , E и F ?
Решение. Имеем кортежи длиной 3 (у треугольника три вершины). Ни один элемент не может входить дважды. Значит,
А 3 5= 
Задачи для домашней работы
Сколько всего различных пятизначных чисел, не содержащих нуля?
В классе изучают девять предметов. Скольки ми способами можно составить расписание на поне дельник, если в этот день должно быть шесть разных уроков?
Перестановка без повторений.
Задача 1. Сколькими способами можно перестав лять друг с другом цифры 1, 2, 3 и 4?
Задача 2. За столом пять мест. Сколькими спосо бами можно рассадить пятерых гостей?
Задача 3. У Лены есть восемь разных красок. Она хочет написать ими слова «Новый Год». Сколькими способами она может это сделать, если каждая буква должна быть раскрашена одним цветом и все восемь букв должны быть разными по цвету?
Решение. Присвоим каждой краске номер от 1 до 8. Тогда каждый искомый способ задается перестанов кой восьми чисел 1, 2, . 8. Значит, таких перестановок 8!. Поэтому она может написать «Новый Год» 8! = 40 320 способами.
Перестановка с повторениями.
Задача 1. У мамы два яблока и три груши. Каж дый день в течение пяти дней она дает сыну по одно му фрукту. Сколькими способами это может быть сделано?
Решение. Р(2, 3) 
Задача 2. Сколькими способами можно положить 28 различных открыток в четыре одинаковых кон верта так, чтобы в каждом конверте было по семь открыток?
Решение. Пометим конверты цифрами 1, 2, 3 и 4. Тогда число различных раскладок равно
Р(7, 7, 7,7)=
Сотрем пометки. Теперь конверты можно произволь но переставлять друг с другом, не меняя результата раскладки (теперь они неотличимы друг от друга). Так как число различных перестановок четырех кон вертов равно
Р 4 = 4!, то число различных раскладок уменьшается в
Р 4 = 4! раз и поэтому оно равно
Ответ:
Задачи для домашней работы
Сколько различных слов можно получить, пе реставляя буквы слова «ингредиент»?
Сколькими способами можно посадить за круг лый стол пять мужчин и пять женщин так, чтобы никакие два лица одного пола не сидели рядом?
Автомобильные номера состоят из четырех цифр и трех букв. Найдите число таких номеров, если используются 32 буквы русского алфавита.
Ответы: 1 .226 800. 2 . 5! ∙ 5! = 14 400. 3. 10 3 ∙32 3 .
Сочетание с повторениями.
Задача 1. В кондитерском отделе продаются пи рожные четырех сортов: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить семь пирожных?
Решение. Здесь рассматриваются сочетания с по вторениями из 4 (четыре вида пирожных) по 7 (столько пирожных покупают). Значит,
Ответ: 120 способов.
Задача 2. В почтовом отделении продают открыт ки 10 видов. Сколькими способами можно купить в нем 12 открыток?
Решение. Здесь рассматриваются сочетания с по вторениями из 10 по 12. Имеем
Сочетания без повторений.
Задача 1. Сколькими способами в игре «Спортло то» можно выбрать шесть номеров из 49?
Решение. Здесь рассматриваются сочетания без повторения (одно число может быть по правилам игры выбрано не более одного раза) из 49 по 6.
Задача 2. У Робина — Бобина Барабека 40 соседей. Он решил пригласить двоих из них на обед. Сколько у него способов это сделать?
Решение. Здесь рассматриваются сочетания без повторений.
Задача 3. Дама сдавала в багаж семь предметов, Все они оказались украденными, но два каких-либо (по ее выбору) ей согласились поискать. Сколько у нее есть возможностей выбрать два любимых предме та?
Задача 4. В прошлые века процветала генуэзская лотерея, сохранившаяся в некоторых странах и поныне. Участники этой лотереи покупали билеты, на которых стояло число от 1 до 90. Можно было ку пить и билеты, на которых было сразу 2, 3, 4 и 5 чисел. В день розыгрыша лотереи из мешка, содержащего жетоны с числами от 1 до 90, вынимали пять жетонов. Выигрывали те, у которых все номера на билетах были среди вынутых. Если участник лотереи покупал билет с одним из чисел, то он получал при выигрыше в 15 раз больше стоимости билета; если с двумя числами (амбо), то в 270 раз больше, если с тремя числами (терн) – в 5500 раз больше, если в четырьмя числами (катерн) – 75000 раз больше, а если с пятью числами (квин) – в 1000 000 раз больше, чем стоит билет. Каково отношение «счастливых» билетов при игре, когда участник купил билет с одним числом?
Решение. Общее число исходов находится из формулы сочетаний без повторений:
С 5 90 =
Если участник купил билет с одним номером, то для выигрыша необходимо, чтобы один из вынутых номеров совпал с номером на билете. Остальные 4 номера могут быть благоприятными. Но эти 4 номера выбираются из оставшихся 89 номеров. Поэтому число благоприятных комбинаций к общему числу комбинаций равно
Ответ:
Задачи для домашней работы
Сочетайте, каково отношение «счастливых» билетов при игре, когда участник купил билет с двумя числами.
Сколькими способами можно составить набор из восьми пирожных, если имеется четыре сорта пирожных?
В классе имеется шесть сильных математиков. Сколькими способами из них можно составить команду на районную олимпиаду по математике, если от класса можно послать команду из четырех человек?
Ответы: 1. 
Источник
комбинаторика
Презентация предназначена в помощь ученикам, пропустившим занатия в школе для самостоятельного изучения темы.
Скачать:
| Вложение | Размер |
|---|---|
| kombinatorika.ppt | 2.53 МБ |
Предварительный просмотр:
Подписи к слайдам:
Комбинаторика Перестановки Размещения Сочетания Презентация выполнена Учеником 10 «а» класса Окуневым Никитой.
Произведения n натуральных чисел от 1 до n обозначается n! ( n факториал ) 1 * 2 * 3 * … * ( n – 1)*n =n! Например: 1*2*3=3! 1*2*3*4*5*6*7*8=8 ! Перестановки Условились считать что: 1!=1 0!=1 Перестановка из n элементов – это расположение их в определённом порядке Например: составим перестановку из х1 х2 х3 х1 х2 х3 х2 х1 х3 х3 х1 х2 х1 х3 х3 х2 х3 х1 х3 х2 х1 Таким образом получаем шесть перестановок
Для любого натурального числа n справедлива формула P n = n! Где P – количество перестановок, а n – число элементов
Задания Вычислите: 7! 5! Ответ: 42
Как – то раз в воскресенье семеро друзей зашли в кафе, уселись за один столик и заказали мороженное. Хозяин кафе сказал, что если друзья в каждое следующее воскресенье будут садиться по новому и перепробуют все способы посадки, то с этого момента он будет кормить их мороженным бесплатно. Удастся ли друзьям воспользоваться предложение ? Ответ: Нет, потому что им нужно будет приходить в кафе 5040 недель 7!=5040
Размещения Размещением из n элементов по k называют любой упорядоченный набор из k элементов , составленный из данных n элементов. Например: составим размещения х1 х2 х3 по 2 х1 х2 х1 х3 х2 х3 х2 х3 х3 х1 х3 х2 Таким образом получилось 9 размещений
n! (n — k)! k A n = n (n — 1)(n — 2)*…*(n – k + 1) A n k Где n – число элементов , а k – число размещений Например: выпишите все размещения из четырёх элементов по два – А 2 4 =4(4 — 1)=4*3=12 А 2 4 = 4 !/ (4 — 2)! = 24/2=12
Задания Вычислите А 7 Ответ: 2520 5 7! (7-5)! 3*4*5*6*7=2520
Сколькими различными способами можно распределить между шестью лицами четыре разные путёвки в санаторий Ответ: 360 6! 2 = 360
Сочетания Сочетанием из данных n элементов по k называют любую группу из k этих элементов Например: из трёх элементов х1 х2 х3 можно составить следующие сочетания по два элемента: х1 х2 х1 х3 х2 х3 Других сочетаний из рассматриваемых элементов по два нет
С n k n! k!(n — k)! Где n – число элементов , а k – число c очетаний Например: Выпишите все сочетания из пяти элементов по два С= 5!/2!(5 — 2)!=120/12=10
Задания Вычислите С 7 5 7! 5!(7-5)! 42 2 24 Ответ:24
Источник
Элементы комбинаторики.



Одно из важнейших правил комбинаторики – правило произведения.
Правило произведения. Если объект A1 может быть выбран k1 способами, затем для каждого из таких выборов объекта A1 другой объект A2 может быть выбран k2 способами, затем для каждого из таких выборов и объекта A1, и объекта A2 третий объект A3 может быть выбран k3 способами и т.д., наконец, объект Am может быть выбран km способами, тогда объект «A1 и A2, и A3, и …, и Am» может быть выбран 
Сочетаниями из n различных элементов по m элементов (m≤n)называют комбинации из m элементов, которые составлены из данных n элементов и отличаются хотя бы одним элементом. Число сочетаний из n элементов по m обозначают 



Пример 1. Сколькими способами между тремя сотрудниками можно распределить две различные путевки?
Решение. Претендент на первую путевку – один из трех сотрудников – может быть выбран тремя способами. Если первая путевка досталась первому сотруднику, то вторая может достаться или второму, или третьему сотруднику. Если первая путевка досталась второму сотруднику, то вторая может достаться или первому, или третьему сотруднику. Если первая путевка досталась третьему сотруднику, то вторая может достаться или первому, или второму сотруднику. Таким образом, для каждого способа распределения первой путевки претендент на вторую путевку может быть выбран двумя способами. Две различные путевки (и первая, и вторая) по правилу произведения могут быть распределены шестью способами:
1) первому и второму сотрудникам;
2) первому и третьему сотрудникам;
3) второму и первому сотрудникам;
4) второму и третьему сотрудникам;
5) третьему и первому сотрудникам;
6) третьему и второму сотрудникам.
Ответ: шестью способами.
Пример 2. Сколькими способами между тремя сотрудниками можно распределить две одинаковые путевки?
Решение. Искомое число равно числу способов выбора из трех сотрудников двух претендентов на путевки. Поскольку 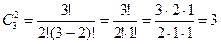
Ответ: тремя способами.
7.1.1. Сколькими способами можно составить флаг, содержащий три горизонтальные полосы различных цветов, если имеется материал пяти цветов? Ответ: 60.
7.1.2. Сколькими способами из группы студентов в двадцать пять человек можно выбрать старосту и физорга? Ответ: 600.
7.1.3. Десять спортсменов разыгрывают одну золотую, одну серебряную и одну бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами? Ответ: 720.
7.1.4. Студентам нужно сдать четыре экзамена за восемь дней. Сколькими способами можно составить расписание сдачи экзаменов? Ответ: 1680.
7.1.5. Сколько словарей нужно издать, чтобы непосредственно выполнить переводы с любого из трех языков: русского, английского, французского — на любой другой из этих трех языков? Ответ: 6.
7.1.6. Сколькими способами можно рассадить на скамейке трех человек? Ответ: 6.
7.1.7. Сколькими способами пять книг разных авторов можно расставить на полке? Ответ: 120.
7.1.8. В конкурсе по пяти номинациям участвуют десять кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены различные призы? одинаковые призы? Ответ: 30240; 252.
7.1.9. В хоккейном турнире участвуют шесть команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире? Ответ: 15.
7.1.10. Сколькими способами читатель может выбрать три книжки из пяти имеющихся различных книг? Ответ: 10.
7.1.11. Сколькими способами можно в строчку написать три плюса и два минуса? Ответ: 10.
7.1.12. В лабораторной клетке содержат пять белых и пять коричневых мышей. Найдите число способов выбора: а) трех мышей, если они могут быть любого цвета; б) трех белых мышей. Ответ: 120; 10.
7.1.13. В ящике двадцать кубиков, среди которых пятнадцать окрашены. Сколькими способами можно взять пять кубиков? пять окрашенных кубиков? Ответ: 15504; 3003.
Источник
















