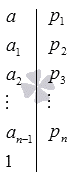Сколько есть способов разложения

Реакции разложения

При выполнении различных заданий ЕГЭ по химии (например, задачи 34 или задания 32 «мысленный эксперимент») могут пригодиться знания о том, какие вещества при нагревании разлагаются и как они разлагаются.

Рассмотрим термическую устойчивость основных классов неорганических веществ. Я не указываю в условиях температуру протекания процессов, так как в ЕГЭ по химии такая информация, как правило, не встречается. Если возможны различные варианты разложения веществ, я привожу наиболее вероятные, на мой взгляд, реакции.

Разложение оксидов

При нагревании разлагаются оксиды тяжелых металлов:

2HgO = 2Hg + O₂

Разложение гидроксидов

Как правило, при нагревании разлагаются нерастворимые гидроксиды. Исключением является гидроксид лития, он растворим, но при нагревании в твердом виде разлагается на оксид и воду:

2LiOH = Li₂O + H₂O

Гидроксиды других щелочных металлов при нагревании не разлагаются.

Гидроксиды серебра (I) и меди (I) неустойчивы:

2AgOH = Ag₂O + H₂O

2CuOH = Cu₂O + H₂O

Гидроксиды большинства металлов при нагревании разлагаются на оксид и воду.

В инертной атмосфере (в отсутствии кислорода воздуха) гидроксиды хрома (III) марганца (II) и железа (II) распадаются на оксид и воду:

Большинство остальных нерастворимых гидроксидов металлов также при нагревании разлагаются:

Разложение кислот

При нагревании разлагаются нерастворимые кислоты.

Например , кремниевая кислота:

Некоторые кислоты неустойчивы и подвергаются разложению в момент образования. Большая часть молекул сернистой кислоты и угольной кислоты распадаются на оксид и воду в момент образования:

В ЕГЭ по химии лучше эти кислоты записывать в виде оксида и воды.

Например , при действии водного раствора углекислого газа на карбонат калия в качестве реагента мы указываем не угольную кислоту, а оксид углерода (IV) и воду, но подразумеваем угольную кислоту при этом:

Азотистая кислота на холоде или при комнатной температуре частично распадается уже в водном растворе, реакция протекает обратимо:

При нагревании выше 100 о С продукты распада несколько отличаются:

Азотная кислота под действием света или при нагревании частично обратимо разлагается:

Разложение солей

Разложение хлоридов

Хлориды щелочных, щелочноземельных металлов, магния, цинка, алюминия и хрома при нагревании не разлагаются.

Хлорид серебра (I) разлагается под действием света:

2AgCl → Ag + Cl₂

Хлорид аммония при нагревании выше 340 о С разлагается:

Разложение нитратов

Нитраты щелочных металлов при нагревании разлагаются до нитрита металла и кислорода.

Например , разложение нитрата калия:

Видеоопыт разложения нитрата калия можно посмотреть здесь.

Нитраты магния, стронция, кальция и бария разлагаются до нитрита и кислорода при нагревании до 500 о С:

При более сильном нагревании (выше 500 о С) нитраты магния, стронция, кальция и бария разлагаются до оксида металла, оксида азота (IV) и кислорода:

Нитраты металлов, расположенных в ряду напряжений после магния и до меди (включительно) + нитрат лития разлагаются при нагревании до оксида металла, диоксида азота и кислорода:

Нитраты серебра и ртути разлагаются при нагревании до металла, диоксида азота и кислорода:

Нитрат аммония разлагается при небольшом нагревании до 270 о С оксида азота (I) и воды:

При более высокой температуре образуются азот и кислород:

Разложение карбонатов и гидрокарбонатов

Карбонаты натрия и калия плавятся при нагревании.

Карбонаты лития, щелочноземельных металлов и магния разлагаются на оксид металла и углекислый газ:

Карбонат аммония разлагается при 30 о С на гидрокарбонат аммония и аммиак:

Гидрокарбонат аммония при дальнейшем нагревании разлагается на аммиак, углекислый газ и воду:

Гидрокарбонаты натрия и калия при нагревании разлагаются на карбонаты, углекислый газ и воду:

Гидрокарбонат кальция при нагревании до 100 о С разлагается на карбонат, углекислый газ и воду:

При нагревании до 1200 о С образуются оксиды:

Разложение сульфатов

Сульфаты щелочных металлов при нагревании не разлагаются.

Сульфаты алюминия, щелочноземельных металлов, меди, железа и магния разлагаются до оксида металла, диоксида серы и кислорода:

Сульфаты серебра и ртути разлагаются до металла, диоксида серы и кислорода:

Разложение фосфатов, гидрофосфатов и дигидрофосфатов

Эти реакции, скорее всего, в ЕГЭ по химии не встретятся! Гидрофосфаты щелочных и щелочноземельных металлов разлагаются до пирофосфатов:

Ортофосфаты при нагревании не разлагаются (кроме фосфата аммония).

Разложение сульфитов

Сульфиты щелочных металлов разлагаются до сульфидов и сульфатов:

Разложение солей аммония

Некоторые соли аммония, не содержащие анионы кислот-сильных окислителей, обратимо разлагаются при нагревании без изменения степени окисления. Это хлорид, бромид, йодид, дигидрофосфат аммония:

Cоли аммония, образованные кислотами-окислителями, при нагревании также разлагаются. При этом протекает окислительно-восстановительная реакция. Это дихромат аммония, нитрат и нитрит аммония:

Видеоопыт разложения нитрита аммония можно посмотреть здесь.

Разложение перманганата калия

Разложение хлората и перхлората калия

Хлорат калия при нагревании разлагается до перхлората и хлорида:

4KClO₃ → 3KClO₄ + KCl

При нагревании в присутствии катализатора (оксид марганца (IV)) образуется хлорид калия и кислород:

2KClO₃ → 2KCl + 3O₂

Перхлорат калия при нагревании разлагается до хлорида и кислорода:

Источник

Разложение чисел на простые множители, способы и примеры разложения

Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.

Что значит разложить число на простые множители?

Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2 · 7 · 7 · 23 имеем, что у нас 4 простых множителя в виде 2 , 7 , 7 , 23 .

Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30 , тогда получим 2 , 3 , 5 . Запись примет вид 30 = 2 · 3 · 5 . Не исключено, что множители могут повторяться. Такое число как 144 имеет 144 = 2 · 2 · 2 · 2 · 3 · 3 .

Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.

При z , относящемуся к целым числам, представляется в виде произведения а и b , где z делится на а и на b . Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1 , то его разложение на множители p 1 , p 2 , … , p n принимает вид a = p 1 , p 2 , … , p n _. Разложение предполагается в единственном варианте.

Каноническое разложение числа на простые множители

При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p 1 , который встречается s 1 раз и так далее p n – s n раз. Таким образом разложение примет вид a=p₁ s ₁· a = p 1 s 1 · p 2 s 2 · … · p n s n . Эта запись имеет название канонического разложения числа на простые множители.

При разложении числа 609840 получим, что 609 840 = 2 · 2 · 2 · 2 · 3 · 3 · 5 · 7 · 11 · 11 ,его канонический вид будет 609 840 = 2 4 · 3 2 · 5 · 7 · 11 2 . При помощи канонического разложения можно найти все делители числа и их количество.

Алгоритм разложения числа на простые множители

Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p 1 , p 2 , … , p n чисел a , a 1 , a 2 , … , a n — 1 , это дает возможность получить a = p 1 · a 1 , где a 1 = a : p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , где a 2 = a 1 : p 2 , … , a = p 1 · p 2 · … · p n · a n , где a n = a n — 1 : p n . При получении a n = 1 , то равенство a = p 1 · p 2 · … · p n получим искомое разложение числа а на простые множители. Заметим, что p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n .

Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z . При взятии простых чисел 2 , 3 , 5 , 11 и так далее, причем на них делим число z . Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z . Видно, что не существуют делителей z , тогда понятно, что z является простым числом.

Рассмотрим на примере числа 87 . При его делении на 2 имеем, что 87 : 2 = 43 с остатком равным 1 . Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87 : 3 = 29 . Отсюда вывод – 3 является наименьшим простым делителем числа 87 .

При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a . При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000 .

Рассмотрим алгоритм разложения на простые множители:

• нахождение наименьшего множителя при делителе p 1 числа a по формуле a 1 = a : p 1 , когда a 1 = 1 , тогда а является простым числом и включено в разложение на множители, когда не равняется 1 , тогда a = p 1 · a 1 и следуем к пункту, находящемуся ниже;
• нахождение простого делителя p 2 числа a 1 при помощи последовательного перебора простых чисел, используя a 2 = a 1 : p 2 _,когда a 2 = 1 , тогда разложение примет вид a = p 1 · p 2 _,когда a 2 = 1 , тогда a = p 1 · p 2 · a 2 _, причем производим переход к следующему шагу;
• перебор простых чисел и нахождение простого делителя p 3 числа a 2 по формуле a 3 = a 2 : p 3 , когда a 3 = 1 , тогда получим, что a = p 1 · p 2 · p 3 _, когда не равняется 1 , тогда a = p 1 · p 2 · p 3 · a 3 и производим переход к следующему шагу;
• производится нахождение простого делителя p n числа a n — 1 при помощи перебора простых чисел с p n — 1 , а также a n = a n — 1 : p n , где a n = 1 , шаг является завершающим, в итоге получаем, что a = p 1 · p 2 · … · p n _.

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.

Полученный алгоритм можно применять при помощи разложения чисел на простые множители.

Примеры разложения на простые множители

Во время разложения на простые множители следует придерживаться основного алгоритма.

Источник

Разложение многочлена способом группировки

О чем эта статья:

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки.
2. Формулы сокращенного умножения.
3. Метод группировки.
4. Выделение полного квадрата.
5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
2. Вынести общий множитель за скобки.
3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

1. Найдем общий множитель: (m — n)
2. Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Источник