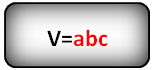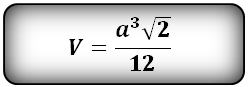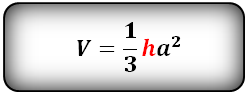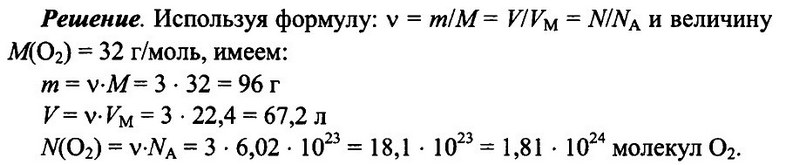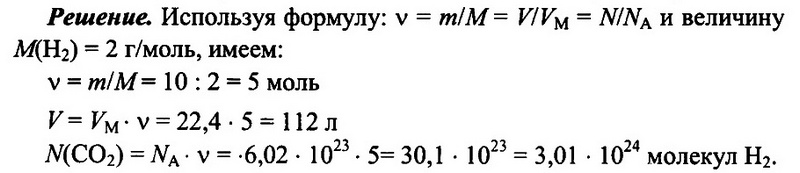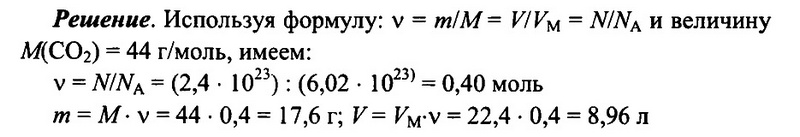Сколько есть способов найти объем

Все формулы объемов геометрических тел

1. Расчет объема куба

a — сторона куба

Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

3. Формула для вычисления объема шара, сферы

R — радиус шара

По формуле, если дан радиус, можно найти объема шара, (V):

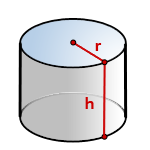
4. Как вычислить объем цилиндра ?

h — высота цилиндра

r — радиус основания

По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):

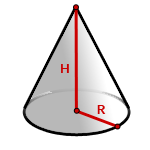
5. Как найти объем конуса ?

R — радиус основания

H — высота конуса

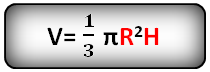
Формула объема конуса, если известны радиус и высота (V):

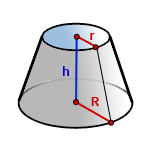
7. Формула объема усеченного конуса

r — радиус верхнего основания

R — радиус нижнего основания

h — высота конуса

Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

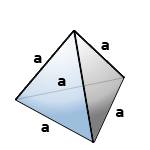
8. Объем правильного тетраэдра

Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.

а — ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

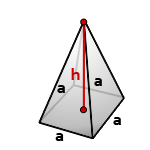
9. Объем правильной четырехугольной пирамиды

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

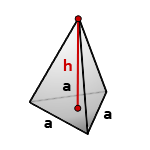
10. Объем правильной треугольной пирамиды

Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):

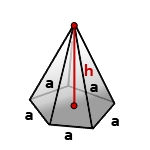
11. Найти объем правильной пирамиды

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

Источник

Сколько есть способов найти объем

Решение задач на количество вещества,
массу и объем

Ключевые слова: решение задач на количество вещества, решение задач по химии на массу и объем, какое количества вещества содержится, какое число молекул содержится, определите объем (н.у.), определите массу, какова масса порции, определите молярную массу, назовите вещество, найдите молярную массу, определите абсолютную массу молекулы, сколько атомов содержится, определите относительную плотность.

ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

Количество вещества характеризует число структурных единиц (атомов, молекул, ионов), которое содержится в определенном образце данного вещества. Единицей измерения количества вещества является моль. Количество вещества (ν) связано с числом структурных единиц (N) в образце вещества, его массой (m) и объемом (V) — для газообразных веществ при н. у. — следующими уравнениями:

в которых

Vm = 22,4 л/моль (мл/ммоль, м 3 /кмоль) при н.у.,
Na = 6,02 • 10 23 (постоянная Авогадро),
а молярная масса (М) численно равна относительной молекулярной массе вещества:

Наличие подобной взаимосвязи позволяет, зная одну из величин (количество вещества, массу, объем, число структурных величин) определить все другие величины.

РЕШЕНИЯ ПРОСТЫХ ЗАДАЧ

Задача № 1. Какое количество вещества содержится в 33 г оксида углерода (IV)?

Ответ: ν(СО₂) = 0,75 моль.

Задача № 2. Какое число молекул содержится в 2,5 моль кислорода?

Ответ: N(O₂) = 1,505 • 10 24 .

Задача № 3. Определите объем (н. у.), который займут 0,25 моль водорода.

Задача № 4. Какую массу будет иметь порция оксида серы (IV), объем которой 13,44 л (н. у.)?

Задача № 5. Имеется 3 моль кислорода О₂ при н.у. Определите массу кислорода, его объем, а также число имеющихся молекул кислорода.

Ответ: m = 96 г; V = 67.2 л; N(O₂) = 1,81 • 10 24 .

Задача № 6. Имеется 10 г водорода Н₂. Определите количество водорода, его объем при н.у., а также число имеющихся молекул водорода.

Ответ: 5 моль; 112 л; 3,01 • 10 24 .

Задача № 7. Имеется 56 л хлора Сl₂ при н.у. Определите количество вещества хлора, его массу и число имеющихся молекул хлора.

Ответ: 2,5 моль; 177,5 г; 1,5 • 10 24 .

Задача № 8. Имеется 2,4 • 10 23 молекул оксида углерода (IV) СO₂. Определите количество вещества углекислого газа, его массу, а также объем (н.у.) углекислого газа.

Ответ: 0,4 моль; 17,6 г; 8,96 л.

Задача № 9. Какова масса порции оксида азота (IV), содержащей 4,816 • 10 23 молекул? Каков ее объем (н. у.)?

Задача № 10. Масса порции простого вещества, содержащей 1,806 • 10 24 молекул, равна 6 г. Определите молярную массу данного вещества и назовите его.

Внимание! В данном конспекте рассматриваются задачи обычной сложности. Чтобы перейти к конспекту решения сложных задач на количественные характеристики и задачи с кратким ответом нажмите на кнопку ниже…

Решение задач на количество вещества, массу и объем. Выберите дальнейшие действия:

Источник

Формула объема.

Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.

Объем фигуры — это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Объемы геометрических фигур.

Параллелепипед.

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

Цилиндр.

Объем цилиндра равен произведению площади основания на высоту.

Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.

Пирамида.

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).

Правильная пирамида — это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

Правильная треугольная пирамида — это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Правильная четырехугольная пирамида — это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Тетраэдр — это пирамида, у которой все грани — равносторонние треугольники.

Усеченная пирамида.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S₁(abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

Куб.

Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 .

Конус — это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Усеченный конус получится, если в конусе провести сечение, параллельное основанию.

V = 1/3 πh (R 2 + Rr + r 2 )

Шар.

Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.

Призма.

Объем призмы равен произведению площади основания призмы, на высоту.

Сектор шара.

Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.

Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.

Сегмент шара — это часть шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом

Источник

Фигура	Формула	Чертеж