Сколькими способами можно закрасить все клетки нарисованные

Сколькими способе можно закрасить все клетки нарисованного справа квадрата при помощи жёлтые зелёные красные красок так чтобы у каждой красные клетки было хотя бы одна общая сторона жёлтый а у жёлтых хотя бы одна общая сторона зелёный использования всех цветов обязательно квадрате вращается

Ответ:

Сначала закрашиваешь две верхние клетки красным, потом левый нижний жёлтым, а правый нижний зелёным. Таким образом, все клетки будут закрашены и будут использованы все цвета!

P.s И у каждого цвета будет общая сторона с другим цветом.

Объяснение:

1.
Const
N = 30;
Var
A:array[1..N] of integer;
i,Max,kMax:integer;
Begin
Randomize;
Write(‘Исходный массив:’);
For i:= 1 to N do
Begin
A[i]:=random(N);
Write(‘ ‘,A[i]);
End;
WriteLn;
<Нахождение максимума>
Max:=A[1];
For i:= 2 to N do
if A[i]>Max then Max:=A[i];
WriteLn(‘Max = ‘,Max);
<Подсчёт максимумов>
kMax:=0;
For i:= 1 to N do
if A[i] = Max then kMax:=kMax+1;
WriteLn(‘kMax = ‘,kMax);
End.

Пример:
Исходный массив: 11 13 9 8 19 9 22 29 0 23 6 26 14 21 24 24 26 26 23 13 12 20 1 21 0 27 25 28 13 0
Max = 29
kMax = 1

2.
Const
N = 30;
Var
A:Array[1..N] of integer;
i,SMax,iSMax:integer;
Begin
Randomize;
Write(‘Исходный массив:’);
For i:= 1 to N do
Begin
A[i]:=random(N);
Write(‘ ‘,A[i])
End;
WriteLn;
iSMax:=1;
SMax:=A[1]+A[2]+A[3];
For i:= 3 to N-2 do
if A[i]+A[i+1]+A[i+2]>SMax then
Begin
iSMax:=i;
SMax:=A[i]+A[i+1]+A[i+2];
End;
WriteLn(‘Номера элементов, сумма которых максимальна: ‘,iSMax,’, ‘,iSMax+1,’, ‘,iSMax+2);
WriteLn(‘Максимальная сумма = A[‘,iSMax,’] + A[‘,iSMax+1,’] + A[‘,iSMax+2,’] = ‘,SMax)
End.

Пример:
Исходный массив: 15 13 25 8 4 4 8 20 26 25 25 7 27 16 28 18 26 24 17 20 7 15 10 12 18 13 22 19 4 25
Номера элементов, сумма которых максимальна: 9, 10, 11
Максимальная сумма = A[9] + A[10] + A[11] = 76

Источник

Подготовка к олимпиаде

Раскраска дома
1. В каждой вершине правильного 100-угольника поставлены фишки: 76 красных и 24 синих. Доказать, что найдутся 4 красные фишки, образующие квадрат.
Решение. Фишки образуют 25 квадратов. Синие фишки являются вершинами не более чем в 24 квадратах, поэтому хотя бы один квадрат будет красным.
2. Клетки прямоугольника 5 × 41 окрашены в два цвета. Доказать, что можно выбрать 3 строки и 3 столбца так, чтобы их пересечения имели один цвет.
Решение. Будем считать, что в прямоугольнике 41 столбец, по пять клеток в каждом. В каждом столбце пометим 3 одноцветные клетки. Это можно сделать 10 способами. Значит, найдется
5 столбцов с одинаково помеченными клетками. Из них хотя бы в трех помечены клетки одного цвета.
3. Клетки таблицы 15 × 15 окрашены в три цвета. Доказать, что найдется 2 строки, в которых клеток одного цвета поровну.
Решение. Допустим противное. Тогда во всех строках клеток каждого цвета разное количество, а всего в таблице клеток одного цвета не менее
0 + 1 + . + 14 = 105; клеток всех трех цветов не менее 315, а в таблице 225 клеток — противоречие.

Найти раскраску
1. Таблицу 4 × 4 раскрасить в 4 цвета так, чтобы на любой горизонтали, вертикали и диагонали были бы все цвета.
Ответ: рис. 1.

2. Сколько клеток таблицы 8 × 8 можно закрасить так, чтобы никакие 3 центра закрашенных клеток не лежали на одной прямой?
Решение. Можно закрасить 16 клеток (рис. 2).

Раскрасить больше 16 клеток нельзя: тогда на какой-то горизонтали появится третья окрашенная клетка.
3. Найти все развертки куба, которыми можно покрыть плоскость без пропусков и перекрытий.
Ответ: плоскость можно покрыть паркетом из фигур, изображенных на рисунке 3.

Сколько способов?
1. Каждую грань кубика разбили на 4 одинаковых квадрата и раскрасили квадраты в несколько цветов так, чтобы квадраты, имеющие общую сторону, были разных цветов. Какое наибольшее количество квадратов одного цвета могло получиться?
Решение. Это количество будет наибольшим, когда боковая поверхность куба покрашена в шахматном порядке. Основание нельзя покрасить в тот цвет, который на боковой поверхности был использован 8 раз (рис. 4).

2. Сколькими способами можно покрасить в 6 цветов грани куба?
Решение. Любую грань можно покрасить в первый цвет (пусть это верхняя грань). Для нижней грани остается 5 вариантов. Любую грань боковой поверхности можно покрасить в третий цвет. Для остальных граней остается 3! = 6 вариантов. Итого: 5×6 = 30.
3. Сколькими способами можно окрасить в 6 цветов 6 равных секторов диска?
Решение. Любой сектор может быть окрашен в любой цвет. Для остальных секторов остается 5! = 120 вариантов.

Раскраска — метод решения

1. Можно ли таблицу 6 × 6 с вырезанными противоположными углами покрыть костями домино размером 1 × 2? Кости не должны перекрываться и выступать за края таблицы.
Решение. Раскрасим таблицу в шахматном порядке (рис. 5).
Получим 18 белых и 16 черных клеток. Кость домино покрывает одну белую и одну черную клетку, следовательно, на доске можно разместить 16 костей, и две белые клетки не будут покрыты доминошками.
2. Учитель попросил ученика вырезать из картонной шахматной доски (8 × 8) 8 квадратов размером 2 × 2 (с условием: не портить оставшиеся клетки). Потом учитель вспомнил, что ему нужно 9 квадратов. Может ли он из остатков доски вырезать девятый квадрат? А десятый?

Решение. Решающее свойство: при вырезании одного квадрата может быть испорчен только один закрашенный. Следовательно, вырезав 8 квадратов, ученик испортил не более 8 закрашенных. Если ученик вырезал 8 закрашенных квадратов, кроме одного углового, то из остатков доски еще один квадрат вырезать можно, а два — не вырезать (рис. 6).

3. Можно ли таблицу 6 × 6 с вырезанными противоположными углами обойти ходом шахматного коня (побывав в каждой клетке один раз)?
Решение. Нет. Клетка, откуда идет конь, и клетка, куда он идет, разного цвета (см. рис. 5).
Эти задачи предлагались школьникам на олимпиадах разных лет. Подобные задачи встречаются в заданиях международной математической олимпиады «Кенгуру».

Источник

сколькими способами можно закрасить ячейки

Ячейки таблицы размером 4 на 4 необходимо закрасить в черный или белый цвет. Напротив каждой строки и каждого столбца записано кильксть черных ячеек, которые должны быть в нем. Нужно определить сколькими разными способами это можно сделать. С клавиатуры (стандартный поток ввода) вводятся две строки целых чисел, разделенных пробелами. Первая строка содержит числа черных ячеек в каждом из четырех строк, а вторая строка — в каждом из четырех столбцов. На экран (стандартный поток вывода) вывести единственное число — количество способов.

Входные данные
2 0 1 1
2 0 1 1

Результат работы
5

Сколькими способами можно построить железную колею длиной N метров
input.txt output.txt Сколькими способами можно построить железную колею длиной N метров, .

Сколькими способами можно зажечь k лампочек?
В комнате n лампочек. Сколькими способами можно зажечь k лампочек? Сколько существует способов.

Сколькими способами можно рассадить гостей?
Иван Иванович пригласил на свой день рождения много гостей. Он написал на карточках фамилии всех.

Сколькими способами можно составить расписание занятий
Напишите программу решения следующей задачи: В седьмом классе изучается 14 предметов. Сколькими.

В комнате n лампочек. Сколькими способами можно зажечь k лампочек?
Помогите плиз. я некоторые задачи решила, но когда наткнулась на эти то, что то не могу понять.

Сколькими способами можно выбрать.?
Сколькими способами можно выбрать 4 набора по 5 карт из колоды, содержащей 52 карты?

Источник

Решение №963 Найдите количество способов закрасить некоторые клетки «лесенки» …

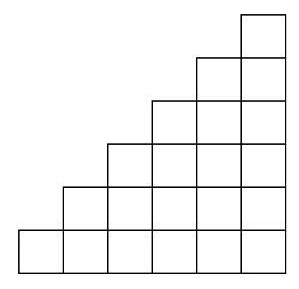
Найдите количество способов закрасить некоторые клетки «лесенки» так, чтобы выполнялись следующие условия:

• Ниже каждой закрашенной клетки либо нет других клеток, либо они все закрашены.

• В одном столбце закрашено 5 клеток, в другом – 4 клетки, в третьем – 3 клетки, …, в последнем – 0 клеток.

Источник задания: ВсОШ sochisirius.ru

Ниже каждой закрашенной клетки либо нет других клеток, либо они все закрашены.

Это условие говорит о том, что нужно начинать закрашивать клетки с нижний и подряд, не пропуская клеток.

5 клеток можем закрасить, только в 2 столбцах на выбор.
4 клетки, учитывая что в одном уже закрашено 5 клеток, можем тоже закрасить в 2 столбцах на выбор.
3 клетки, учитывая, что есть столбец с 5 клетками и 4 клетками, тоже 2 способами. И так далее..
2 клетки – 2 способами.
1 клетку – 2 способами.
0 клеток – 1 способом (останется один столбец)

Тогда всего вариантов:

2·2·2·2·2·1 = 32

Ответ: 32.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.8 / 5. Количество оценок: 6

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Источник

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

Главный Попко

2 комбинаторные задачки. 9 класс. Помогите пожалуйста, заранее благодарна)№1 Сколькими способами можно закрасить 6 клеток таким образом, чтобы 3 клетки были красными, а 3 оставшиеся были закрашены (каждая своим цветом) белым, черным, зеленым?№2 Сколькими способами из 10 игроков волейбольной команды можно выбрать стартовую 6-ку?

Лучший ответ:

Зачетный Опарыш

№2. сочетание из 10 по 6.

№1 Выберем три клетки из шести. Это можно сделать сочетания из шести по три.
И закрасим их красным цветом. Из оставшихся трех выбираем одну и красим её белым цветом. Тогда имеем сочетание из шести по три, умножить на сочетание из трех по одному. Поскольку цветов три. умножим это на три. Клетку можем закрасить как белым, так и зеленым и черным цветом.
Теперь из оставшихся двух клеток выбираем одну и закрашиваем ее одним из двух оставших цветов ( черным или зеленым).
А если выбрали в предыдущий выбор зеленый ( то теперь белый или черный)
И если выбрали в предыдущий выбор черный цвет ( то теперь белый и зеленый)
Итак сочетание из шести по три умножаем на 3 на сочетание из трех по одному на 2 и на сочетание из двух по одному. Это в числителе.

А в знаменателе, наверное перестановка из шести.

Источник