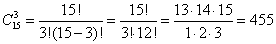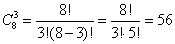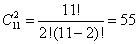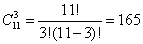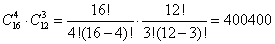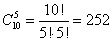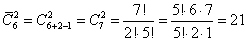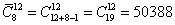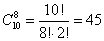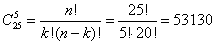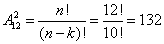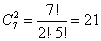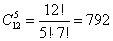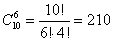КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m (

Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Источник
Первичное закрепление
6. Первичное закрепление
Давайте сначала выясним, чем отличаются размещения от сочетаний? В сочетаниях порядок элементов не важен, а размещениях – важен!
Задача 1. Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Решение: каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3. Следовательно, по формуле получаем
Задача 2. В магазине «Филателия» продается 8 различных марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
Задача 3. На полке стоит 12 книг: англо-русский словарь и 11 художественных произведений на английском языке. Сколькими способами читатель может выбрать 3 книги, если :
а) словарь нужен ему обязательно;
б) словарь ему не нужен?
а)
б)
Задача 4. В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков и трех девочек. Сколькими способами это можно сделать?
Решение:
Задача 5. На тренировках занимаются 10 баскетболистов. Сколько различных стартовых пятерок может образовать тренер?
Решение.
Задача 6. Сколько наборов из семи пирожных можно составить, если в продаже имеется четыре сорта пирожных?
Решение. 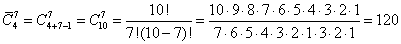
Задача 7. Сколько существует различных треугольников, длины сторон которых принимают значения: 8, 10, 12 и 14 см? Сколько среди них равносторонних, равнобедренных, разносторонних?
Решение: число различных треугольников равно числу сочетаний с повторениями из четырех элементов по три: 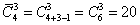
Из них количество разносторонних треугольников равно числу сочетаний без повторений их четырех элементов по три, т.е.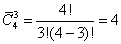
Задача 8. Сколько всего существует результатов опыта, заключающегося в подбрасывании двух одинаковых игральных костей?
Решение.
Задача 9. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? 8 открыток? 8 различных открыток?
Решение. 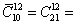
— Что нового вы сегодня узнали на уроке?
— Чем отличаются сочетания от размещений? (сочетания – порядок не важен, размещения – порядок важен!)
Урок 10. Урок-практикум. Подготовка к контрольной работе
· подготовить учащихся к контрольной работе с помощью решения задач и повторения некоторых теоретических вопросов;
Оборудование: карточки с задачами.
1. Сообщение темы и целей
Сегодня на уроке мы будем готовиться к контрольной работе: решать задачи и повторять теорию
2. Домашнее задание
Подготовиться к контрольной работе
1. Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить … способами. (m+n)
2. Кортежи длины k, составленные из элементов п-множества, называют размещениями … из п элементов по k. (с повторениями)
3. Два … из п элементов по т отличаются друг от друга хотя бы одним элементом. (сочетания)
1. «Вороне где-то Бог послал кусочек сыра», колбасы, хлеба и шоколада. «На ель Ворона взгромоздясь, позавтракать совсем уж было собралась, да призадумалась»: если есть кусочки по очереди, то из скольких вариантов придется выбирать?
2. Сколькими способами можно из 25 учащихся выбрать 5 для участия в школьном марафоне?
3. Сколькими способами могут быть распределены золотая и серебряная медали по итогам первенства по футболу, если число команд 12?
4. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
5. Из 12 солдат нужно в разведку послать 5. Сколькими способами это можно сделать?
6. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из этого списка 6 книг?
7. Назовем симпатичными числа, в записи которых используют только нечетные числа. Сколько существует четырехзначных симпатичных чисел?
8. Сколько пятизначных чисел можно составить, используя только цифры 3 и 5?
9. «Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». Сколькими способами они могут распределить четыре имеющихся у них инструмента?
10. «Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». На складе 12 музыкальных инструментов. Мишке поручили принести со склада 8 любых инструментов. Сколько вариантов выбора есть у мишки?
11. Гера, Афина и Афродита попросили Париса не только назвать самую красивую из них, но и указать, кто «на втором и третьем местах». Сколько есть вариантов ответа?
12. Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
13. В магазине «Филателия» продается 8 различных наборов марок, посвященных «Дню Победы». Сколькими способами можно сформировать из них 3 набора?
14. Сколько существует способов составить расписание уроков на один день из 6 предметов?
15. Алфавит племени тумба-юмба состоит из букв А, У, С. Словом является любая последовательность из 4 букв. Сколько слов в языке этого племени?
16. Сколькими способами можно выложить в ряд красный, зеленый, черный, синий кубики?
17. Из колоды в 36 карт вынимают 5 карт. Найдите число всех возможных вариантов выбора.
18. В классе 27 учеников, из которых нужно выбрать троих: первый ученик должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую. Сколькими способами это можно сделать?
Ответы и решения к задачам
2.
3.
4.
5.
6.
Источник