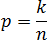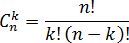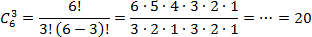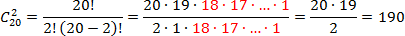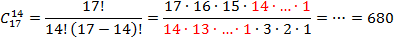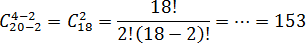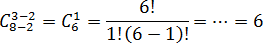Правила комбинаторики в задаче B6
29 декабря 2011
Решая задачи по теории вероятностей, мы постоянно используем одну и ту же формулу, которая одновременно является классическим определением вероятности:
где k — число благоприятных исходов, n — общее число исходов (см. «Тест по теории вероятностей»).
И эта формула прекрасно работает до тех пор, пока задачи были легкими, а числа, стоящие в числителе и знаменателе — очевидными.
Однако последние пробные экзамены показали, что в настоящем ЕГЭ по математике могут встречаться значительно более сложные конструкции. Отыскание значений становится проблематичным. В таком случае на помощь приходит комбинаторика. Ее законы работают там, где искомые значения не выводятся непосредственно из текста задачи.
В сегодняшнем уроке не будет строгих формулировок и длинных теорем — они слишком сложны и, к тому же, совершенно бесполезны для решения настоящих задач B6. Вместо этого мы рассмотрим простые правила и разберем конкретные задачи, которые действительно встречаются на ЕГЭ. Итак, поехали!
Число сочетаний и факториалы
Пусть имеется n объектов (карандашей, конфет, бутылок водки — чего угодно), из которых требуется выбрать различных объектов. Тогда количество вариантов такого выбора называется элементов Это число обозначается и считается по специальной формуле.
Выражение n ! читается как «эн-факториал» и обозначает произведение всех натуральных чисел включительно:
Кроме того, в математике по определению считают, подобный бред редко, но все же встречается в задачах по теории вероятностей.
Что дает нам эта формула? На самом деле, без нее не решается практически ни одна серьезная задача.
К сожалению, в школе совершенно не умеют работать с факториалами. Кроме того, в формуле числа сочетаний очень легко запутаться: где стоит и что обозначает Поэтому для начала просто запомните: меньшее число всегда стоит сверху — точно так же, как и в формуле определения вероятности (вероятность никогда не бывает больше единицы).
Для лучшего понимания разберем несколько простейших комбинаторных задач:
Задача. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?
Тут все просто: есть n = 6 сортов, из которых надо выбрать сорта. Число сочетаний можно найти по формуле:
Задача. В группе из 20 студентов надо выбрать 2 представителей для выступления на конференции. Сколькими способами можно это сделать?
Опять же, всего у нас есть n = 20 студентов, а выбрать надо студента. Находим число сочетаний:
Обратите внимание: красным цветом отмечены множители, входящие в разные факториалы. Эти множители можно безболезненно сократить и тем самым значительно уменьшить общий объем вычислений.
Задача. На склад завезли 17 серверов с различными дефектами, которые стоят в 2 раза дешевле нормальных серверов. Директор купил в школу 14 таких серверов, а сэкономленные деньги своровал и купил дочке шубу из меха соболя за 200 000 рублей. Сколькими способами директор может выбрать бракованные серверы?
В задаче довольно много лишних данных, которые могут сбить с толку. Наиболее важные факты: всего есть серверов, а директору надо серверов. Считаем число сочетаний:
Красным цветом снова обозначены множители, которые сокращаются. Итого, получилось 680 комбинаций. В общем, директору есть из чего выбрать.
Как видите, число сочетаний из n по k считается достаточно просто. Проблема в том, что многие школьники никогда не работали с факториалами. Для них это новый и незнакомый математический объект, и для его освоения требуется некоторая тренировка.
Хорошая новость состоит в том, что во многих задачах формулы оказывается вполне достаточно для нахождения ответа. Но есть и плохая новость: в тех редких случаях, когда нужны дополнительные правила, решение задачи резко усложняется. Эти правила мы сейчас и рассмотрим.
Закон умножения
в комбинаторике: число сочетаний (способов, комбинаций) в независимых наборах умножается.
Другими словами, пусть имеется A способов выполнить одно действие выполнить другое действие. Путь также эти действия независимы, т.е. никак не связаны между собой. Тогда можно найти число способов выполнить первое и второе действие по формуле:
Задача. У Пети есть 4 монеты по 1 рублю и 2 монеты по 10 рублей. Петя, не глядя, достал из кармана 1 монету номиналом 1 рубль и еще 1 монету номиналом 10 рублей, чтобы купить сигарету за 11 рублей у бабули в подземном переходе. Сколькими способами он может выбрать эти монеты?
Итак, сначала Петя достает монету имеющихся монет номиналом 1 рубль. Число способов сделать это равно
Затем Петя снова лезет в карман и достает монету имеющихся монет номиналом 10 рублей. Здесь число сочетаний равно
Поскольку эти действия независимы, общее число вариантов равно
Задача. В корзине лежат 8 белых шаров и 12 черных. Сколькими способами можно достать из этой корзины 2 белых шара и 2 черных?
Всего в корзине белых шаров, из которых надо выбрать шара. Это можно сделать различными способами.
Кроме того, в корзине имеется черных шаров, из которых надо выбрать опять же шара. Число способов сделать это равно
Поскольку выбор белого шара и выбор черного — события независимые, общее число комбинаций считается по закону умножения: Как видим, вариантов может быть довольно много.
Закон умножения показывает, сколькими способами можно выполнить сложное действие, которое состоит из двух и более простых — при условии, что все они независимы.
Именно этой формулы многим не хватило для решения задачи B6 на пробном ЕГЭ по математике. Разумеется, существуют и другие методы решения, в которых комбинаторика не используется — и мы обязательно рассмотрим их ближе к настоящему экзамену. Однако ни один из них не сравнится по надежности и лаконичности с теми приемами, которые мы сейчас изучаем.
Закон сложения
Если закон умножения оперирует «изолированными» событиями, которые не зависят друг от друга, то в законе сложения все наоборот. Здесь рассматриваются взаимоисключающие события, которые никогда не случаются одновременно.
Например, «Петя вынул из кармана 1 монету» и «Петя не вынул из кармана ни одной монеты» — это взаимоисключающие события, поскольку вынуть одну монету и при этом не вынуть ни одной невозможно.
Аналогично, события «Выбранный наугад шар — белый» и «Выбранный наугад шар — черный» также являются взаимоисключающими.
в комбинаторике: если два взаимоисключающих действия можно выполнить способами соответственно, то эти события можно объединить. При этом возникнет новое событие, которое можно выполнить способами.
Другими словами, при объединении взаимоисключающих действий (событий, вариантов) число их комбинаций складывается.
Можно сказать, что закон сложения — это логическое «ИЛИ» в комбинаторике, когда нас устраивает любой из взаимоисключающих вариантов. И наоборот, закон умножения — это логическое «И», при котором нас интересует одновременное выполнение и первого, и второго действия.
Задача. В корзине лежат 9 черных шаров и 7 красных. Мальчик достает 2 шара одинакового цвета. Сколькими способами он может это сделать?
Если шары одинакового цвета, то вариантов немного: оба они либо черные, либо красные. Очевидно, что эти варианты — взаимоисключающие.
В первом случае мальчику предстоит выбирать черных шара имеющихся. Число способов сделать это равно
Аналогично, во втором случае выбираем красных шара возможных. Число способов равно
Осталось найти общее количество способов. Поскольку варианты с черными и красными шарами — взаимоисключающие, по закону сложения имеем:
Задача. В ларьке продаются 15 роз и 18 тюльпанов. Ученик хочет купить 3 цветка для своей одноклассницы, причем все цветы должны быть одинаковыми. Сколькими способами он может составить такой букет?
По условию, все цветы должны быть одинаковыми. Значит, будем покупать либо 3 розы, либо 3 тюльпана. В любом случае,
В случае с розами придется выбирать вариантов, поэтому число сочетаний равно Для тюльпанов же а число сочетаний —
Поскольку розы и тюльпаны — это взаимоисключающие варианты, работаем по закону сложения. Получаем общее число вариантов Это и есть ответ.
Дополнительные условия и ограничения
Очень часто в тексте задачи присутствуют дополнительные условия, накладывающие существенные ограничения на интересующие нас сочетания. Сравните два предложения:
- Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа?
- Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа, если среди них обязательно должен быть красный цвет?
Чувствуете разницу? В первом случае мы вправе брать любые цвета, какие нам нравятся — дополнительных ограничений нет. Во втором случае все сложнее, поскольку мы обязаны выбрать ручку красного цвета (предполагается, что она есть в исходном наборе).
Очевидно, что любые ограничения резко сокращают итоговое количество вариантов. Ну и как в этом случае найти число сочетаний? Просто запомните следующее правило:
Пусть имеется набор элементов, среди которых надо выбрать При введении дополнительных ограничений числа уменьшаются на одинаковую величину.
Другими словами, если из 5 ручек надо выбрать 3, при этом одна из них должна быть красной, то выбирать придется элементов элемента. Таким образом, вместо надо считать
Теперь посмотрим, как это правило работает на конкретных примерах:
Задача. В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участия в конференции. Сколькими способами можно выбрать этих четверых, если отличники обязательно должны попасть на конференцию?
Итак, есть группа студентов. Но выбрать надо из них. Если бы не было дополнительных ограничений, то количество вариантов равнялось числу сочетаний
Однако нам поставили дополнительное условие: 2 отличника должны быть среди этих четырех. Таким образом, согласно приведенному выше правилу, мы уменьшаем числа на 2. Имеем:
Задача. У Пети в кармане есть 8 монет, из которых 6 монет по рублю и 2 монеты по 10 рублей. Петя перекладывает какие-то три монеты в другой карман. Сколькими способами Петя может это сделать, если известно, что обе монеты по 10 рублей оказались в другом кармане?
Итак, есть монет. Петя перекладывает монеты, из которых 2 — десятирублевые. Получается, что из 3 монет, которые будут переложены, 2 уже зафиксированы, поэтому числа надо уменьшить на 2. Имеем:
В обоих примерах я намеренно пропустил детали работы с факториалами — попробуйте выполнить все расчеты самостоятельно. Разумеется, для этих задач существуют и другие способы решения. Например, с помощью закона умножения. В любом случае, ответ будет один и тот же.
В заключение отмечу, что в первой задаче мы получили 153 варианта — это намного меньше, чем исходные вариантов. Аналогично, 3 монеты из 8 можно переложить способами, что значительно больше 6 способов, которые мы получили в последней задаче.
Эти примеры наглядно демонстрируют, что введение любых ограничений значительно сокращает нашу «свободу выбора».
Источник
Схемы выбора конечного числа элементов из заданного множества.
Дата добавления: 2014-03-24 ; просмотров: 9268 ; Нарушение авторских прав
Правило умножения и правило сложения.
Комбинаторика.
История возникновения теории вероятностей.
Предмет теории вероятностей.
6. Элементы комбинаторики: сочетание, размещение, перестановка.
Каждодневный опыт убеждает нас в том, что в обыденной жизни, практических ситуациях, а также в научных исследованиях постоянно приходится сталкиваться с положениями, когда привычные нам закономерности строгого детерминизма, уже не имеют места. При решении многих задач нам приходится учитывать и случайные факторы, придающие исходу элемент неопределенности. Например, при стрельбе из орудия по цели наблюдается так называемое рассеивание снарядов. Уклонение очки попадания снаряда от центра цели заранее указать нет возможности – оно случайно. Невозможно предсказать, какая сторона выпадет при бросании монеты. Одной констатации факта наличия случайности для уверенного использования явлений природы или управления технологическими процессами совершенно недостаточно, необходимо научиться количественно оценивать случайные явления, прогнозировать их течение. Этим занимаются две математические науки – теория вероятностей и математическая статистика.
Теория вероятностей – математическая наука, изучающая закономерности, присущие массовым случайным явлениям.
Предметом теории вероятностей являются математические модели случайных явлений. То есть теория вероятностей рассматривает не сами реальные явления, а их упрощенные схемы – математические модели. Под случайным явлением понимают явление, предсказать исход которого невозможно (при неоднократном воспроизведении одного и того же опыта оно протекает каждый раз несколько по-иному).
Возникновение теории вероятностей относится к середине 17 в. и связано с попыткой создания теории азартных игр. Первую книгу по теории вероятностей «О расчетах в азартной игре» опубликовал голландский математик Х.Гюйгенс. Становление теории вероятностей как науки связано с именами Якоба Бернулли, К. Гаусса, П Лапласа, С. Пуассона. Ученые были убеждены в том, что на базе массовых случайных явлений могут возникать четкие закономерности.
С половины 19 столения развитие теории вероятностей связано в значительной мере с именами русских ученых – В.Я Бунявского ( был написан им первый в Росси курс теории вероятностей), П.Л.Чебышева, А.А.Маркова, А.М.Ляпунова. ими было введено в качестве объекта систематического изучения и широко использовано понятие случайной величины.
В настоящее время нет практически ни одной области науки, в которой в той или иной степени не применялись бы вероятностные методы.
Во многих задачах классической теории вероятностей используется комбинаторика – раздел математики, в котором изучаются различные соединения (комбинации) элементов конечных множеств.
Многие комбинаторные задачи могут быть решены с помощью двух важных правил:
1. Правило умножения: если из некоторого конечного множества первый объект (элемент ) можно выбрать способами, а второй объект (элемент ) — способами, то оба объекта ( и ) в указанном порядке можно выбрать способами.
Это правило распространяется на случай трех и более объектов.
Пример. Сколькими способами могут быть распределены три призовых места среди 16 соревнующихся?
Решение. Имеется 16 различных способов распределения 1-го места. После того как первое место занято, осталось 15 соревнующихся, претендующих на 2-ое место. После занятия второго места, осталось 14 спортсменов, претендующих на 3-е место. Так как нам надо распределить 1-ое и 2-ое и 3-е места среди соревнующихся, то воспользуемся правилом умножения: (способов).
Ответ. Существует 3360 способов распределения трех призовых мест среди 16 соревнующихся.
Пример. Если подбросить одновременно три игральные кости, то сколько имеется различных возможных комбинаций выбранных очков?
Решение. Первая кость – 6 возможных комбинаций, вторая кость – 6 возможных комбинаций, третья кость – 6 возможных комбинаций. Так как одновременно подбрасываются 1-ая кость и 2-я и 3-я, то воспользуемся правилом умножения: (способов).
Ответ. При подбрасывании одновременно трех игральных костей имеется 216 способов различных возможных комбинаций выпавших очков.
2. Правило сложения: если некоторый объект можно выбрать способами, а объект — способами, причем первые и вторые способы не пересекаются, то любой из указанных объектов ( или ) можно выбрать способами.
Данное правило распространяется на любое конечное число объектов.
Пример. Сколькими способами можно выбрать один цветок из корзины, в которой имеется 12 гвоздик, 15 роз и 7 хризантем?
Решение. Одну гвоздику мы можем выбрать 12 способами, одну розу – 15 способами, одну хризантему – 7 способами. Так как выбрать надо только один цветок из корзины, то это будет или 1 гвоздика или 1 роза или 1 хризантема. Воспользуемся правилом сложения: 12+15+7=34 (способа).
Ответ. Один цветок из корзины можно выбрать 34 способами.
Пример. В студенческой группе 12 девушек и 16 юношей. Сколькими способами можно выбрать для вручения призов двух студентов одного пола?
Решение. Сначала найдем сколькими способами для вручения призов можно выбрать двух девушек их 12. Воспользуемся правилом умножения: (способа). Теперь найдем сколькими способами можно выбрать двух юношей: (способов). Так как по условию задачи призы вручают или две девушки или два юноши, то воспользуемся правилом сложения: 132+240=372 способа.
Ответ. Для вручения призов двух студентов одного пола можно выбрать 372 способами.
Решение вероятностных задач часто облегчается, если использовать комбинаторные формулы. Каждая из них определяет число всевозможных исходов в некотором опыте, состоящем в выборе наудачу элементов из различных элементов рассматриваемого множества.
Существует две схемы выбора элементов ( ) из исходного множества:
· без возвращения – выбранные элементы не возвращаются в исходное множество;
· с возвращением – выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.
Элементы комбинаторики (схема выбора без возвращения).
Пусть имеется множество из различных элементов, т.е. элементы имеют или разные названия или разные номера. Пусть , .
Определение. Сочетанием из элементов по элементов называется любое подмножество, которое содержит элементов, взятых из данных элементов.
Из определения следует, что сочетания – это выборки (комбинации), каждая из которых состоит из элементов, взятых из данных элементов, и которые различаются друг от друга только элементами, входящими в них; порядок, в котором они расположены не имеет значения.
Число различных сочетаний из элементов по можно найти по формуле
Значения могут быть найдены не расчетом по формуле количества сочетаний, а с помощью так называемого треугольника Паскаля (Блез Паскаль (1623 – 1662) – французский математик).
Источник