Сколькими способами можно выбрать четырехзначное число все числа которого различны

Задачи по комбинаторике. Часть 1

В этой статье использован материал из лекций Шарича Владимира Златковича и Максимова Дмитрия Васильевича на КПК foxford.

Очень рекомендую абитуриентам курсы foxford для подготовки к ЕГЭ и олимпиадам.

1. Сколько четырехзначных чисел содержит ровно одну семерку?

Четырехзначное число имеет вид . Если четырехзначное число содержит ровно одну семерку, то она может стоять

1) на первом месте, и тогда на остальных трех местах могут стоять любые цифры от 0 до 9, кроме цифры 7, и по правилу произведения мы получаем четырехзначных чисел, у которых семерка стоит на первом месте.

2) на любом месте, кроме первого, и тогда по правилу произведения мы получаем . У нас три возможности расположения цифры 7, на первом месте может стоять 8 цифр (все цифры, кроме нуля и 7), на тех местах, где не стоит цифра 7 — 9 цифр.

Сложим полученные варианты, и получим четырехзначных чисел, содержащих ровно одну семерку.

2. Сколько пятизначных чисел содержит ровно две семерки?

Так же как в предыдущей задаче у нас две возможности:

1) Одна из семерок стоит на первом месте, а вторая на любом из оставшихся четырех мест. На трех местах, не занятых цифрой 7 может стоять любая из 9 цифр (все, кроме цифры 7). В этом случае мы получаем чисел.

2) Ни одна из семерок не стоит на первом месте. В этом случае мы имеем возможностей расставить 2 семерки на оставшихся 4-х местах. У нас осталось 3 места, не занятых цифрой 7, одно из которых первое, и таким образом мы получаем чисел.

Сложим полученные варианты, и получим пятизначных чисел, содержащих ровно две семерки.

3. Сколько существует пятизначных чисел, цифры которых различны и расположены в порядке возрастания?

Так как первой цифрой не может быть 0, рассмотрим последовательность цифр 1-9, расположенных в порядке возрастания.

1, 2, 3, 4, 5, 6, 7, 8, 9

Если мы выберем из этой последовательности 5 произвольных цифр, например так:

1, 2 , 3, 4 , 5, 6, 7 , 8 , 9

то получим пятизначное число, цифры которого различны и расположены в порядке возрастания.

Осталось посчитать, сколькими способами мы можем выбрать из 9 цифр 5:

Итак существует 126 пятизначных чисел, цифры которых различны и расположены в порядке возрастания.

Треугольник Паскаля и число сочетаний.

4. Задача о хромом короле. Пусть есть доска размером . Король находится в левом верхнем углу доски и может перемещаться по доске, двигаясь только вправо и вниз. Сколькими способами король может добраться до левого нижнего угла доски?

Посчитаем, для каждой клетки, сколькими способами король может до нее добраться.

Так как король может двигаться только вправо и вниз, до любой клетки первого столбца и первой строки он может добраться единственным способом:

Рассмотрим произвольную клетку доски. Если в клетку, стоящую над ней можно добраться способами, а в клетку, стоящую слева от нее способами, то в саму клетку можно добраться способами (это следует из того, что король может двигаться только вправо и вниз, то есть не может дважды зайти на одну клетку):

Заполним начальные клетки, пользуясь этим правилом:

Мы видим, что при заполнении клеток у нас получается треугольник Паскаля, только повернутый на бок.

Число в каждой клетке показывает, сколькими способами король может попасть в эту клетку из левой верхней.

Например, чтобы попасть в клетку (4;3) — четвертая строка, третий столбец, король должен сделать 4-1=3 шага вправо, и 3-1=2 шага вниз. То есть всего 3+2=5 шагов. Нам нужно найти число возможных последовательностей этих шагов:

То есть найти, скольким способами мы можем расположить 2 вертикальные (или 3 горизонтальные) стрелки на 5-ти местах. Число способов равно:

— то есть ровно то число, которое стоит в этой клетке.

Для того, чтобы попасть в последнюю клетку, король должен сделать всего шага, из которых по вертикали. Таким образом, он может попасть в последнюю клетку

Можно получить рекуррентное соотношение для числа сочетаний:

Смысл этого соотношения следующий. Путь у нас есть множество, состоящее из n элементов. И нам нужно выбрать из этого множества l элементов. Все способы, которыми мы можем это сделать делятся на две группы, которые не пересекаются. Мы можем:

а) зафиксировать один элемент, и из оставшихся n-1-го элемента выбрать l-1 элемент. Это можно сделать способами.

б) выбрать из оставшихся n-1-го элемента все l элементов. Это можно сделать способами.

Также можно получить соотношение:

Действительно, левая часть этого равенства показывает число способов выбрать какое-то подмножество из множества, содержащего n элементов. (Подмножество, содержащее 0 элементов, 1 элемент и так далее.) Если мы пронумеруем n элементов, то получим цепочку из n нулей и единиц, в которой 0 означает, что данные элемент не выбран, а 1 — что выбран. Всего таких комбинаций, состоящих из нулей и единиц .

Кроме того, число подмножеств с четным числом элементов равно числу подмножеств с нечетным числом элементов:

Докажем это соотношение. Для этого докажем, что между подмножествами с четным числом элементов и подмножествами с нечетным числом элементов существует взаимно однозначное соответствие.

Зафиксируем один элемент множества:

Теперь возьмем произвольное подмножество, и если оно не содержит этот элемент, то поставим ему в соответствие подмножество, состоящее из тех же элементов, что и выбранное, плюс этот элемент. А если выбранное подмножество уже содержит это элемент, то поставим ему в соответствие подмножество, состоящее из тех же элементов, что и выбранное, минус этот элемент. Очевидно, что из этих пар подмножеств одно содержит четное число элементов, а другое — нечетное.

5. Рассмотрим выражение

1. Сколько слагаемых имеет этот многочлен?

а) до приведения подобных членов

б) после приведения подобных членов.

2. Найти коэффициент при произведении

При возведении суммы слагаемых в степень , мы должны эту сумму умножить на себя раз. Мы получаем сумму одночленов, степень каждого из которых равна m. Число всевозможных произведений, состоящих из переменных из множества с учетом порядка и возможностью повторения равно числу размещений с повторениями из k по m:

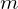
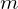
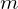
Когда мы приводим подобные члены, мы считаем одинаковыми произведения, содержащие равное число множителей каждого вида. В этом случае, чтобы найти число слагаемых многочлена после приведения подобных членов, мы должны найти число сочетаний с повторениями из k по m:

Найдем коэффициент при произведении .

Выражение представляет собой произведение m элементов из множества , причем элемент взят раз, элемент взят раз, и так далее, и, наконец, элемент взят раз. Коэффициент при произведении равен числу возможных произведений:

Рассмотрим частный случай: — Бином Ньютона. И получим формулу для биномиальных коэффициентов.

Произвольный член многочлена, полученного возведением двучлена в степень имеет вид , где А — биномиальный коэффициент, . Как мы уже получили,

Тогда если мы положим х=1 и y=1, то получим, что

6. Задача про кузнечика.

Есть n клеточек, расположенных последовательно. Кузнечик должен попасть из крайней левой клеточки в крайнюю правую, прыгая вправо на произвольное число клеток.

а) Сколькими способами он может это сделать?

Изобразим условие задачи:

Кузнечик может попасть в крайнюю правую клетку, побывав, или не побывав в любой внутренней клетке. Присвоим клетке значение 1, если кузнечик в ней побывал, и 0, если нет, например, так:

Тогда у нас есть n-2 клеточек, каждая из которых может принимать значение 0 или 1. Задача сводится к нахождению числа последовательностей, состоящих из n-2 нулей и единиц. Таких последовательностей .

б) сколькими способами кузнечик может добраться в n-ю клетку, сделав k шагов?

Чтобы попасть в n-ю клетку, сделав k шагов, кузнечик должен попасть ровно в k—1 клетку между первой и последней. Так как последний шаг он делает всегда в последнюю клетку. То есть стоит вопрос, сколькими способами можно выбрать k—1 клетку из n-2 клеток?

Ответ: .

в) сколькими способами кузнечик может добраться в n-ю клетку, двигаясь на одну или на две клетки вправо?

Распишем, сколькими способами можно попасть в каждую клетку.

В первую и вторую клетки можно попасть единственным способом: в первую — никуда из нее не уходя, и во вторую из первой:

В третью можно попасть из первой или второй, то есть двумя способами:

В четвертую — из второй или третьей, то есть 1+2=3 способами:

В пятую — из третьей или четвертой, то есть 2+3=5 способами: Можно заметить закономерность: чтобы найти число способов, которыми кузнечик может попасть в клетку с номером k нужно сложить число способов, которыми кузнечик может попасть в две предыдущие клетки:

Мы получили интересную последовательность чисел — числа Фибоначчи — это линейная рекуррентная последовательность натуральных чисел, где первое и второе равно единице, а каждое последующее — сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.

Источник