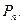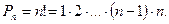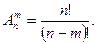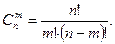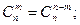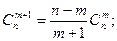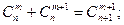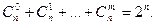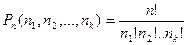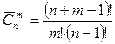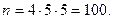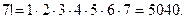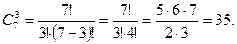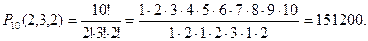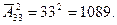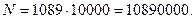Математика
определения и теоремы, учебная литература, решение задач и примеров
Задачи на вероятность (Часть 1)
Задачи на вероятность. Элементы комбинаторики. Часть 1.
Для решения большинства задач на вероятность (по теории вероятностей) необходимы базовые знание комбинаторики (понятия сочетаний, перестановок, размещений). Ниже представлен ряд задач по комбинаторике, которые являются некой подготовкой к решению задач по теории вероятностей.
Задача 1. (Ниворожкина, Морозова. Основы статистики с элементами теории вероятностей)
Правление коммерческого банка выбирает из 10 кандидатов 3 человек на различные должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?
В условии задачи речь идет о расчете числа комбинаций из 10 элементов по 3. Так как группы по 3 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т.е. порядком, то для ответа необходимо рассчитать число размещений из 10 элементов по 3:
N = A 3 10 = 10·9·8=720.
Ответ. Можно составить 720 групп по 3 человека из 10.
Задача 2. (Ниворожкина, Морозова. Основы статистики с элементами теории вероятностей)
Правление коммерческого банка выбирает из 10 кандидатов 3 человек на одинаковые должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?
Состав различных групп должен отличаться по крайней мере хотя бы одним кандидатом и порядок выбора кандидата не имеет значения, следовательно, этот вид соединений представляет собой сочетания. По условию задачи n = 10, m = 3.
Получаем C 3 10 = 10!/3!7! = 120.
Ответ. Можно составить 120 групп из 3 человек по 10.
Задача 3. (Ниворожкина, Морозова. Основы статистики с элементами теории вероятностей)
Сколькими способами можно выбрать 6 пирожных в кондитерской, где есть 4 разных сорта пирожных?
Это случай сочетания с повторениями.
Ответ. Существует 84 различных способа выбора пирожных.
Задача 4. (Ниворожкина, Морозова. Основы статистики с элементами теории вероятностей)
Менеджер ежедневно просматривает 6 изданий экономического содержания. Если порядок просмотра изданий случаен, то сколько существует способов его осуществления?
Способы просмотра изданий различаются только порядком, так как число, а значит, и состав изданий при каждом способе неизменны. Следовательно, при решении этой задачи необходимо рассчитать число перестановок.
По условию задачи n = 6. Следовательно,
Рn = 6! =1·2·3·4·5·6 = 720.
Ответ. Можно просмотреть издания 720 способами.
а) Сколько существует способов составления в случайном порядке списка из 7 кандидатов для выбора на руководящую должность?
б) Какова вероятность того, что кандидаты будут расставлены в списке по возрасту (от меньшего к большему)?
а) Так как порядок случаен, то количество способов равно числу перестановок из 7 человек:
P = 7! = 7 ⋅6⋅5⋅4⋅3⋅2⋅1 = 5040 (способов).
б) в предположении, что у всех кандидатов возрасты различные, то есть не найдется двух и более человек с одинаковым возрастом, количество способов расставить всех кандидатов по возрасту равно 1. Поэтому вероятность равна:
P = 1/5040 = 0,0002.
Ответ: а) 5040; б) 1/5040.
Модельер, разрабатывающий новую коллекцию одежды к весеннему сезону, создает модели в зеленой, черной и красной цветовой гамме. Вероятность того, что зеленый цвет будет в моде весной, модельер оценивает в 0,3, что черный — в 0,2, а вероятность того, что будет моден красный цвет — в 0,15. Предполагая, что цвета выбираются независимо друг от друга, оцените вероятность того, что цветовое решение коллекции будет удачным хотя бы по одному из выбранных цветов?
p1 = 0,3 — вероятность того, что зеленый цвет будет в моде,
p2 = 0,2 — вероятность того, что черный цвет будет в моде,
p3 = 0,15 — вероятность того, что красный цвет будет в моде.
Событие А — цветовое решение удачно хотя бы по одному из выбранных цветов.
Тогда вероятность P(A) будет равна:
P(A) = 1 — q1q2q3 = 1 — (1-p1)(1-p2)(1-p3) = 1-0,7 ⋅0,8⋅0,85 = 0,524.
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Этот сайт использует Akismet для борьбы со спамом. Узнайте как обрабатываются ваши данные комментариев.
Источник
Комбинаторика
Основные понятия и формулы
Какое-либо упорядоченное множество, которое состоит из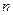 
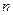
элементов, называется перестановкой из элементов, и обозначается 
Формула перестановки 
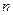
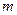
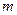
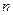
Размещением из элементов по 
, называется некоторое упорядоченное подмножество из элементов множества из элементов.
Формула размещений 
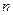
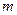
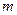
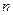
Сочетанием из по называется некое подмножество из элементов некоторого множества из .
Формула сочетаний 
Свойства сочетаний:
1. 
2. 
3. 
4. 
Перестановки с повторением, если среди n элементов есть одинаковые, и если среди них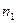 
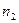
— первого типа, 
— другого типа и т. д., то получаем формулу для перестановок с повторением.
Формула перестановки с повторением 
Размещение с повторением – это упорядоченное подмножество, дге элементы не обязательно должны быть разными.
Формула размещение с повторением: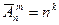 
.
Сочетания с повторением – это подмножество, элементы которого не обязательно должны быть разными.
Формула сочетания с повторением: 
Пример 1. Сколько трехзначных чисел можно записать цифрами 0,1,2,3,4?
Первая цифра в трехзначном числе может быть выбрана 4 способами (0 не выбирается), другая цифра 5 способами, третья тоже 5 способами. По правилу произведения все три цифры можно выбрать 
Пример 2. Сколькими способами 7 человек могут встать в очередь в кассу?
Число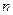 
равно числу перестановок из 7 элементов. 
Пример 3. Сколькими способами можно из 7 человек выбрать комиссию из 3 человек?
Поскольку порядок среди выбранных в комиссию человек не важен, то число способов равно сочетанию из 7 по 3. 
Пример 4.Сколько разных слов можно образовать перестановками букв в слове «математика»?
В слове «математика» — 10 букв, из них буква «м» повторяется 2 раза, «а» — 3 раза, «т» — 2 раза. Тогда используя формулу перестановок с повторением получим ответ:
Пример 5.Автомобильный номер состоит из двух букв и 4 цифр. Какое число номеров можно составить, если буквы выбирают из 33 букв украинского алфавита?
Найдем отдельно комбинации для букв и отдельно для чисел.
Для букв используем размещения с повторением: 
Для цифр: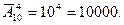 
Тогда 
Пример 6.Сколькими способами можно выбрать 6 одинаковых или разных пироженных в кондитерской, где есть 11 разных сортов пироженных?
Источник
Игра «Звездный час» по теме: «Комбинаторика»
Цель изучения темы «Комбинаторика»: формирование основных понятий комбинаторики и методов решения комбинаторных задач.
-овладеть понятием множества и операциями над множествами;
-познакомить с Биномом Ньютона;
-рассмотреть применение комбинаторики к теории вероятности.
Цель проведения игры: выявление степени усвоения учащимися изученного материала по теме «Комбинаторика».
— плакат «Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердь Пойа, венгерский математик
— на доске звезды с цифрами, которые показывают уровень сложности задачи (на обратной стороне текст задачи; тексты задач в нескольких вариантах, так как одну и ту же звезду могут выбрать несколько учащихся)
Внимание! Внимание!
Скорей берись за дело!
Даешь соревнование
Смекалистых, умелых.
Уже готово все к сражению
Команды лишь сигнала ждут.
Одну минуточку терпения –
Мы вам представим грозный суд.
Приветствие жюри командами.
О жюри, родное, строгое такое,
Мы хотим пропеть вам
Небольшой романс.
Если станет скучно.
Если станет грустно,
Ты зови, зови к себе всех нас.
Будь же справедливым,
Самым неподкупным
И очко — другое незаметно припиши.
Ведь тебя не зря мы нежно называем
Птичкой на ветвях своей души.
Трудный конкурс впереди, строгое жюри,
Но соперники твои уж не так страшны.
Если будешь помнить ты истину одну –
Смелый и решительный не идет ко дну.
Болельщики, предупреждаем,
Что будет встреча горяча.
И потому мы вам желаем
Болеть без вызова врача.
Сойдемся в дружеском турнире,
Раздайтесь, стены, вдоль и ввысь.
Итак: «Вперед!» — звучит в эфире.
Эй, как там, все ли собрались?»
Учащиеся выбирают звезду, решают задачу, затем берут следующую.
В конце игры жюри подводит итоги, выявляя самых смекалистых. Трое учащихся получают грамоты за призовые места, остальные – сертификат участника. (Можно поощрить учащихся отметками)
1 (2 балла). Сколькими способами можно выбрать 6 разных пирожных в кондитерской, где есть 11 разных сортов пирожных?
2 (2 балла). Сколькими способами могут разместиться 5 покупателей в очереди в кассу?
3 (3 балла). Из цифр 0,1,2 составлены всевозможные трехзначные числа без повторения цифр. Сколько получилось чисел?
4 (4 балла). Записать формулу (а + в) 4 .
Ответ. а 4 + 4а 3 в + 6а 2 в 2 + 4ав 3 + в 4 .
5 (5 баллов). За одним столом надо рассадить 5 мальчиков и 5 девочек так, чтобы не было двух рядом сидящих мальчиков и двух рядом сидящих девочек. Сколькими способами это можно сделать?
Ответ. 28800 (2*Р5*Р5 =2 * (120) 2 =2 * 14400 =28800)
6 (4 балла). На собрании должны выступать 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов при условии, что А должен выступать непосредственно перед Б?
7 (4 балла). Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?
8 (5 баллов). Из 20 сотрудников лаборатории 5 человек должны выехать в командировку. Сколько может быть различных составов отъезжающей группы, если заведующий лабораторией и два ведущих инженера одновременно уезжать не должны?
Ответ.15368 составов (С20 5 – С20 2 =15368)
9 (3 балла). Сколькими способами могут быть присуждены 1-я, 2-я и 3-я премии трем лицам, если число соревнующихся равно 10?
10 (5баллов). Решить уравнение: Ах 2 – Сх 1 = 0.
11 (4 балла). Из цифр 0, 1, 2, 3, 4 составлены всевозможные пятизначные числа так, в каждом числе нет одинаковых цифр. Сколько получилось чисел?
Источник
