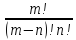Сколькими способами можно установить дежурство по одному человеку

Практическая работа: «Комбинаторика»

Работа для проверки знаний по теме «Комбинаторика».

Просмотр содержимого документа
«Практическая работа: «Комбинаторика»»

Практическая работа: «Комбинаторика»

Практическая работа: «Комбинаторика»

Сколькими способами можно рассадить пятерых детей на пяти стульях в столовой детского сада?

Сколькими способами можно установить дежурство по одному человеку в день среди 6 (5, 7) учащихся класса в течение 6 (5, 7) дней?

Сколько различных семизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 0, 1, 2, 3, 4, 5, 6 так чтобы: 1) последней была цифра 0, 2) первой была цифра 4, 3) первой цифра 3, а последней цифра 5?

1. Сколькими способами можно рассадить пятерых детей на пяти стульях в столовой детского сада?

2. Сколькими способами можно установить дежурство по одному человеку в день среди 4 (8, 9) учащихся класса в течение 4 (8, 9) дней?

3. Сколько различных восьмизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7 так чтобы: 1) последней была цифра 0, 2) первой была цифра 4, 3) первой цифра 3, а последней цифра 5?

Сколько существует способов для обозначения с помощью букв A, B, C, D, E, F, G вершин данного: 1) треугольника, 2) пятиугольника?

В классе 25 учеников. Сколькими способами из их числа можно сделать назначение: 1) физорга и культорга, 2) физорга, культорга и казначея?

В шахматном турнире участвуют: 1) 6 юношей и 2 девушки, 2) 5 юношей и 3 девушки. Сколькими способами могут распределиться места среди участников, если все наберут разное количество очков?

Сколько существует способов для обозначения с помощью букв A, B, C, D, E, F, G вершин данного: 1) четырехугольника, 2) шестиугольника?

В классе 27 учеников. Сколькими способами из их числа можно сделать назначение: 1) физорга и культорга, 2) физорга, культорга и казначея?

3. В шахматном турнире участвуют: 1) 7 юношей и 2 девушки, 2)5 юношей и 4 девушки. Сколькими способами могут распределиться места среди участников, если все наберут разное количество очков?

3. Сочетания С n _m =

1. Сколькими способами для участия в соревнованиях из 9 человек можно выбрать: 1) 4 студентов, 2) 5 студентов?

2. На плоскости отмечено: 1) 16 точек, 2) 13 точек, причем никакие 3 из низ не лежат на одной прямой. Сколько различных отрезков можно построить, соединяя эти точки попарно?

3. На окружности отмечено: 1) 7 точек, 2) 8 точек. Сколько различных треугольников с вершинами, выбранными из этих точек, можно построить?

3. Сочетания С n _m =

1. Сколькими способами для участия в соревнованиях из 11 человек можно выбрать: 1) 6 студентов, 2) 7 студентов?

2. На плоскости отмечено: 1) 15 точек, 2) 14 точек, причем никакие 3 из низ не лежат на одной прямой. Сколько различных отрезков можно построить, соединяя эти точки попарно?

3. На окружности отмечено: 1) 5 точек, 2) 10 точек. Сколько различных треугольников с вершинами, выбранными из этих точек, можно построить?

Источник

Сколькими разными способами можно назначить двух ребят на дежурство по столовой если в классе 24 человека?

Математика | 5 — 9 классы

Сколькими разными способами можно назначить двух ребят на дежурство по столовой если в классе 24 человека.

Напишите пожалуйста как можно записать объяснения решения в тетрадь.

И получаешь сколько пар у тебя будет на каждое дежурство.

В классе 12 мальчиков и 10 девочек?

В классе 12 мальчиков и 10 девочек.

Сколькими способами можна назначить одного дежурного в этом классе?

Нужно объяснение, решение и ответ.

Помогите пожалуйста решить задачу для 6 класса :сколькими разными способами можно назначить двух ребят на дежурство по столовой, если в классе 25 учащихся?

Помогите пожалуйста решить задачу для 6 класса :

сколькими разными способами можно назначить двух ребят на дежурство по столовой, если в классе 25 учащихся?

С решением пожалуйста

обязательно выберу лучший ответ.

В классе 13 девочек и 10 мальчиков?

В классе 13 девочек и 10 мальчиков.

Сколькими различными способами можно назначить двух дежурных (мальчик + девочка)?

Сколькими разными способами можно назначить двух ребят на дежурство по столовой, если в классе 25 учащихся?

Сколькими разными способами можно назначить двух ребят на дежурство по столовой, если в классе 25 учащихся?

Я знаю что ответ 300.

Но как найти 300 и откуда не пнимаю помогите срочно надо).

В классе 12 девочек и 16 мальчиков?

В классе 12 девочек и 16 мальчиков.

Сколькими способами можно выбрать двух ребят одного пола для дежурства по классу?

В 4″Б» учится 25 человек?

В 4″Б» учится 25 человек.

Сколькими способами можно назначить двух дежурных по классу.

Реши задачу : в двух пачках 240 тетрадей, причём в одной из них в три раза больше чем в другой?

Реши задачу : в двух пачках 240 тетрадей, причём в одной из них в три раза больше чем в другой.

Сколько тетрадей в каждой пачке И решение как записать.

В июне 7 ребят из нашего класса поедут в лагерь, 15 — на дачи, четверо останутся дома?

В июне 7 ребят из нашего класса поедут в лагерь, 15 — на дачи, четверо останутся дома.

Сколько учеников в нашем классе?

Помогите записать решение задачи разными способами.

Для дежурства в классе в течение недели выделены 6уч?

Для дежурства в классе в течение недели выделены 6уч.

Сколькими способами можно установить очередность дежурств, если каждый уч.

В июне 7 ребят из нашего класса поедут в лагерь, 15 — на дачи, четверо останутся дома?

В июне 7 ребят из нашего класса поедут в лагерь, 15 — на дачи, четверо останутся дома.

Сколько учеников в нашем классе?

Помогите записать решение задачи разными способами.

Вы открыли страницу вопроса Сколькими разными способами можно назначить двух ребят на дежурство по столовой если в классе 24 человека?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

= — 0, 96b + 3 — 2, 9b + 8 — 16 + 6b = ( — 0, 96b — 2, 9b + 6b) + (3 + 8 — 16) = 2, 14b — 5 приb = — 9 / 13 2, 14 * ( — 9 / 13) — 5 = 214 / 100 * ( — 9 / 13) — 5 = — 1 313 / 650 — 5 = — 6 313 / 650 Пояснение : 214 / 100 * ( — 9 / 13) = — 1926 / 1300 ..

S = π * r² площадь круга S = 3, 14 * 5² = 3, 14 * 25 = 78, 5см² площадь круга 10 * 10 = 100см² площадь квадрата 100 — 78, 5 = 21, 5см² площадь закрашенной части квадрата.

S = 1 × a×h — 2 Нужно просто сосчитать клетки . S = 1×4×10 = 20 см в квадрате — 2.

Икс — 17 = 36 Икс = 36 + 17 Икс = 53.

X — 17 = 36 x = 36 + 17 x = 53 Ответ : 53.

R = 3 (радиус) l = 4 (образующая) Площадь боковой поверхности конуса находится по формуле : S = pi * R * l = 12 * pi.

Решений систем уравнений с помощью матриц. 1)Методом Гаусса 2)Метод Крамера 3)Методом обратной матрицы.

Сложение и умножение : 56 + 78 ; 8 * 7 ; 76 + 6.

18 / 90 = 2 / 10 = 1 / 5 Или 18 / 90 = 9 / 45 = 1 / 5.

Источник

Практическое занятие на тему «Основные комбинаторные конфигурации»

Практическое занятие (2ч.)

Тема: Основные комбинаторные конфигурации .

научить применять комбинаторные конфигурации при решении задач;

сформировать умение находить нужную комбинаторную формулу при решении задачи;

формирование самостоятельности студента на занятии.

Математика / приложение к газете «Первое сентября», №15, 2004 г.

Стойлова Л.П. Математика.-М.: Изд. Центр Академия, 1997.

Прикладная комбинаторная математика.

Вариативная самостоятельная работа.

Повторение основных формул необходимых при решении комбинаторных задач.

Размещения с повторениями.

Задача 1. Сколько различных четырехзначных чи­ сел можно составить из цифр 2, 6, 7, 8 и 9, если каждая цифра может входить в комбинацию несколько раз?

Решение. Здесь порядок цифр существенен (2678 или 6278 — это разные числа). Поэтому имеем дело с кортежем длины 4 (четырехзначное число), каждый элемент которого можно выбрать пятью способами (цифр дано пять). Поэтому число различных комби­ наций равно 4 5 = 1024.

Задача 2. На референдуме предложены четыре вопроса, на которые надо ответить «да» или «нет». Сколько есть возможностей заполнения бюллетеня (на все вопросы надо дать ответ)?

Решение. Получаем кортеж длины 4 (столько во­ просов в бюллетене), каждый элемент может быть вы­ бран двумя способами («да» или «нет»). Поэтому число различных возможностей равно 2 4 =16.

Задача 3 . Неудовлетворенные решением Париса Гера, Афина и Афродита обратились к трем мудре­ цам с просьбой назвать прекраснейшую из них. Каж­ дый из мудрецов высказал свое мнение. Сколько мог­ ло возникнуть вариантов ответа на поставленный во­ прос у этой тройки?

Решение. Здесь вновь кортеж длиной 3 (три муд­ реца), каждый элемент которого может быть выбран шестью способами. Поэтому число различных возмож­ ностей равно 6 3 = 216.

Задача 4 . У Лены есть восемь красок. Она хочет написать ими слова «Новый Год». Сколькими спосо­ бами она может это сделать, если собирается каждую букву раскрашивать одним цветом?

Решение . Кортеж длиной 8 (восемь букв), каждый элемент может быть выбран восемью способами (во­ семь красок). Поэтому число способов равно 8 8 .

Задача 5. На железнодорожной станции имеется я семафоров. Сколько может быть дано различных сигналов при помощи этих семафоров, если каждый семафор имеет три состояния: горит либо зеленый, либо желтый, либо красный свет.

Решение. Имеем кортеж длины n (дано n семафо­ ров), каждый элемент которого можно выбрать тре­ мя способами (каждый семафор имеет три состояния). Поэтому различных сигналов можно дать 3 n .

Задачи для домашней работы

Сколько букв русского алфавита можно зако дировать, используя лишь комбинации точек и тире, содержащие только три знака?

Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать?

Задача 1. Из спортивного клуба, насчитывающего 30 членов, надо составить команду из четырех чело­ век для участия в эстафете на 100 + 200 + 400 + 800 (м). Сколькими способами это можно сделать?

Решение. Имеем кортежи длиной 4. Ни один эле­мент не может входить дважды (один бегун на один отрезок дистанции). Значит,

А 4 ₃₀ = =27·28·29·30 = 657 720.

Задача 2. Сколькими способами можно обозначить вершины данного треугольника, используя буквы А, В, С, D , E и F ?

Решение. Имеем кортежи длиной 3 (у треугольни­ка три вершины). Ни один элемент не может входить дважды. Значит,

А 3 ₅₌

Задачи для домашней работы

Сколько всего различных пятизначных чисел, не содержащих нуля?

В классе изучают девять предметов. Скольки ми способами можно составить расписание на поне­ дельник, если в этот день должно быть шесть разных уроков?

Перестановка без повторений.

Задача 1. Сколькими способами можно перестав­ лять друг с другом цифры 1, 2, 3 и 4?

Задача 2. За столом пять мест. Сколькими спосо­ бами можно рассадить пятерых гостей?

Задача 3. У Лены есть восемь разных красок. Она хочет написать ими слова «Новый Год». Сколькими способами она может это сделать, если каждая буква должна быть раскрашена одним цветом и все восемь букв должны быть разными по цвету?

Решение. Присвоим каждой краске номер от 1 до 8. Тогда каждый искомый способ задается перестанов­ кой восьми чисел 1, 2, . 8. Значит, таких переста­новок 8!. Поэтому она может написать «Новый Год» 8! = 40 320 способами.

Перестановка с повторениями.

Задача 1. У мамы два яблока и три груши. Каж­ дый день в течение пяти дней она дает сыну по одно­ му фрукту. Сколькими способами это может быть сделано?

Решение. Р(2, 3) = 10.

Задача 2. Сколькими способами можно положить 28 различных открыток в четыре одинаковых кон­ верта так, чтобы в каждом конверте было по семь открыток?

Решение. Пометим конверты цифрами 1, 2, 3 и 4. Тогда число различных раскладок равно

Р(7, 7, 7,7)=.

Сотрем пометки. Теперь конверты можно произволь­ но переставлять друг с другом, не меняя результата раскладки (теперь они неотличимы друг от друга). Так как число различных перестановок четырех кон­ вертов равно

Р ₄ = 4!, то число различных раскладок уменьшается в

Р ₄ = 4! раз и поэтому оно равно

Ответ:

Задачи для домашней работы

Сколько различных слов можно получить, пе реставляя буквы слова «ингредиент»?

Сколькими способами можно посадить за круг­ лый стол пять мужчин и пять женщин так, чтобы никакие два лица одного пола не сидели рядом?

Автомобильные номера состоят из четырех цифр и трех букв. Найдите число таких номеров, если ис­пользуются 32 буквы русского алфавита.

Ответы: 1 .226 800. 2 . 5! ∙ 5! = 14 400. 3. 10 3 ∙32 3 .

Сочетание с повторениями.

Задача 1. В кондитерском отделе продаются пи­ рожные четырех сортов: наполеоны, эклеры, песоч­ные и слоеные. Сколькими способами можно купить семь пирожных?

Решение. Здесь рассматриваются сочетания с по­ вторениями из 4 (четыре вида пирожных) по 7 (столько пирожных покупают). Значит,

Ответ: 120 способов.

Задача 2. В почтовом отделении продают открыт­ ки 10 видов. Сколькими способами можно купить в нем 12 открыток?

Решение. Здесь рассматриваются сочетания с по­ вторениями из 10 по 12. Имеем

Сочетания без повторений.

Задача 1. Сколькими способами в игре «Спортло­ то» можно выбрать шесть номеров из 49?

Решение. Здесь рассматриваются сочетания без повторения (одно число может быть по правилам игры выбрано не более одного раза) из 49 по 6.

Задача 2. У Робина — Бобина Барабека 40 соседей. Он решил пригласить двоих из них на обед. Сколько у него способов это сделать?

Решение. Здесь рассматриваются сочетания без повторений.

Задача 3. Дама сдавала в багаж семь предметов, Все они оказались украденными, но два каких-либо (по ее выбору) ей согласились поискать. Сколько у нее есть возможностей выбрать два любимых предме­ та?

Задача 4. В прошлые века процветала генуэзская лотерея, сохранившаяся в некоторых странах и по­ныне. Участники этой лотереи покупали билеты, на которых стояло число от 1 до 90. Можно было ку­ пить и билеты, на которых было сразу 2, 3, 4 и 5 чисел. В день розыгрыша лотереи из мешка, содер­жащего жетоны с числами от 1 до 90, вынимали пять жетонов. Выигрывали те, у которых все номера на билетах были среди вынутых. Если участник лотереи покупал билет с одним из чисел, то он получал при выигрыше в 15 раз больше стоимости билета; если с двумя числами (амбо), то в 270 раз больше, если с тремя числами (терн) – в 5500 раз больше, если в четырьмя числами (катерн) – 75000 раз больше, а если с пятью числами (квин) – в 1000 000 раз больше, чем стоит билет. Каково отношение «счастливых» билетов при игре, когда участник купил билет с одним числом?

Решение. Общее число исходов находится из формулы сочетаний без повторений:

С 5 ₉₀ =

Если участник купил билет с одним номером, то для выигрыша необходимо, чтобы один из вынутых номеров совпал с номером на билете. Остальные 4 номера могут быть благоприятными. Но эти 4 номера выбираются из оставшихся 89 номеров. Поэтому число благоприятных комбинаций к общему числу комбинаций равно

Ответ:

Задачи для домашней работы

Сочетайте, каково отношение «счастливых» билетов при игре, когда участник купил билет с двумя числами.

Сколькими способами можно составить набор из восьми пирожных, если имеется четыре сорта пирожных?

В классе имеется шесть сильных математиков. Сколькими способами из них можно составить команду на районную олимпиаду по математике, если от класса можно послать команду из четырех человек?

Ответы: 1. . 2. 165. 3. 15.

Источник