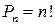13. Перестановки с повторениями
При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет 
. Мы имеем здесь дело с перестановками с повторениями.
Общую задачу сформулируем следующим образом.
Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, 
. Сколько можно составить различных перестановок из этих элементов?
Число перестановок c повторениями обозначают 
. Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом 
способами так, что она остаётся неизменной.
Число различных перестановок с повторениями, которые можно составить из данных элементов, равно
, (11.1) где 
.
Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:
.
Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем
.
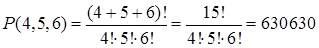
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?
Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:
.
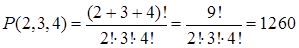
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем
.
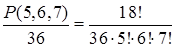
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?
Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим
.
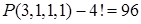
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить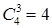 
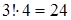
способами. Всего получаем 
способа.
11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?
Ответ: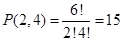 
.
11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?
Ответ: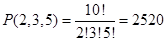 
.
11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?
Ответ: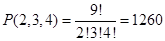 
.
11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?
Ответ: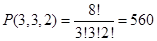 
.
11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?
Ответ: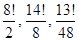 
.
11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?
Ответ: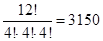 
.
11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
Ответ: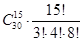 
.
11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?
Ответ: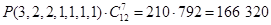 
.
11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать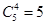 
способами. Всего 
способов.
Источник
Формулы комбинаторики
Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций, получаемых из элементов данного множества.
Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами суммы и произведения.
Правило суммы: Если объект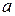 
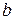
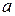
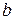
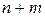
может быть выбран из совокупности объектов 
способами, и после каждого такого выбора объект 
может быть выбран 
способами, то выбрать либо , либо можно 
способами.
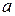
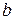
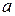
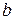
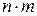
Правило произведения: Если объект может быть выбран из совокупности объектов способами, и после каждого такого выбора объект может быть выбран способами, то пару объектов , в указанном порядке можно выбрать 
способами.
Пример 5. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
Решение. По правилу произведения двух девушек можно выбрать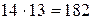 
способами, а двух юношей – 
способами. Следует выбрать двух студентов одного пола: двух девушек или двух юношей. Согласно правилу сложения число таких способов выбора будет: 182+30=212.
1. Перестановки.
Перестановками называют комбинации, составленные из различных элементов и отличающиеся друг от друга только порядком расположения элементов.
Число всех перестановок из элементов вычисляется по формуле
Перестановки с повторениями: если один элемент повторяется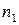 
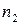
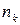
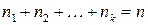
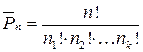
раз, второй элемент повторяется 
раз, к-тый элемент повторяется 
раз, а всего элементов 
, то число комбинаций будет равно:
.
Пример. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение. Так как каждый вариант жеребьевки отличается только порядком выступления участников, то для подсчета числа различных вариантов следует воспользоваться формулой перестановок:
, то есть 5040 перестановок.
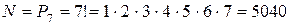
Пример. Сколько различных пятизначных чисел можно составить из цифр 3, 3, 5, 5, 8?
Решение.Каждое пятизначное число отличается только порядком следования цифр, причем цифра 3 встречается 2 раза, цифра 5 – 2 раза, а цифра 8 – 1 раз, то есть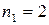 
, 
, 
, 
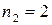
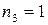
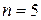
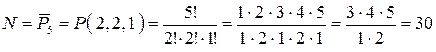
. Для подсчета числа различных пятизначных чисел следует воспользоваться формулой перестановок с повторениями:
, то есть
30 различных пятизначных цифр.
2. Размещения.
Размещениями называются комбинации, составленные из n различных элементов по различным элементам, которые отличаются либо составом элементов, либо порядком их расположения.
Число различных размещений из n элементов по элементам определяется формулой:
.
Размещения с повторениями: если каждый элемент может быть использован раз, то число размещений с повторениями будет равно:
.
Пример. На кодовом замке 10 кнопок. Код состоит из трех различных цифр. Сколько различных кодов можно набрать?
Решение.Так как при наборе трехзначного кода можно набирать 3 цифры из имеющихся 10 в любом порядке, то есть коды могут отличаться либо составом цифр, либо порядком их расположения, то для подсчета числа различных кодов воспользуемся формулой размещений:
, то есть
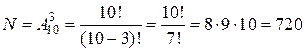
720 различных кодов.
Пример. Пять человек вошли в лифт на первом этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
Решение.Каждый из пяти пассажиров может выйти на любом из восьми этажей со 2-го по 9-й включительно. Так как все пассажиры могут выйти на разных этажах, а могут на каком-то этаже выйти несколько пассажиров (например, на втором этаже вышел один пассажир, на четвертом – один, и трое вышли на восьмом этаже), то для подсчета числа способов выхода 5 пассажиров из лифта следует воспользоваться формулой размещения с повторениями:
.
Такой же результат можно получить, используя правило умножения: для первого пассажира имеется 8 вариантов выхода на этаже, для второго тоже 8, и для третьего – 8, и для четвертого – 8, и для пятого – 8. Всего получается: 
вариантов выхода 5-ти пассажиров.
3. Сочетания.
Сочетаниями называются комбинации, составленные из n различных элементов по m элементам, отличающиеся друг от друга только составом элементов.
В сочетаниях, в отличие от размещений, не учитывается порядок элементов. Число сочетаний из n элементов по m элементов вычисляется по формуле
.
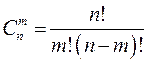
Сочетания с повторениями: если каждый элемент из n элементов может быть использован m раз, то число сочетаний с повторениями будет равно:
.
Пример. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? Сколькими способами можно выбрать 1 красную гвоздику и 2 розовых?
Решение.Так как порядок выбора цветов не имеет значение, то выбрать 3 цветка из вазы, в которой стоят 14 гвоздик, можно 
способами.
.
Красную гвоздику из 10 имеющихся можно выбрать 10 способами или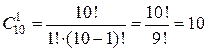 
. Выбрать две розовые гвоздики из имеющихся четырех можно 
способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить (по правилу умножения) 
способами.
Пример. В магазине имеется 7 видов тортов. Сколькими способами можно составить набор, содержащий 3 торта? А если имеются 3 вида тортов, а нужен набор из 7 тортов?
Решение.Поскольку порядок расположения тортов в наборе не играет роли, то искомое число наборов равно числу сочетаний с повторениями из 7 элементов по 3 в каждом:
;
Если имеется 3 вида тортов, а нужен набор из 7 тортов, то число возможных наборов равно:
.
Урновые схемы
Есть урна, (то есть ящик), содержащая n занумерованных объектов, которые мы будем называть шариками. Мы выбираем из этой урны k шариков. Нас интересует, сколькими способами можно выбрать k шариков из n, или сколько различных результатов (то есть наборов, состоящих из k шариков) получится.
На этот вопрос нельзя дать однозначный ответ, пока мы не определимся
– с тем, как организован выбор (скажем, можно ли шарики возвращать в урну), и
– с тем, что понимается под различными результатами выбора.
Рассмотрим следующие возможные схемы выбора:
1. Выбор с возвращением: каждый выбранный шарик возвращается в урну, то есть каждый из k шариков выбирается из полной урны. В полученном наборе, состоящем из k номеров шариков, могут встречаться одни и те же номера (выборка с повторениями).
2. Выбор без возвращения: выбранные шарики в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера (выборка без повторений).
И в том, и в другом случае результатом выбора является набор из k номеров шариков. Удобно считать, что шарики всегда выбираются последовательно, по одному (с возвращением или без).
Условимся, какие результаты мы будем считать различными.
Есть две возможности:
1. Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трех шариков из урны, содержащей 5 шариков, наборы (1,2,5), (2,5,1) (4,4,5) различны, если производится выбор с учетом порядка.
2. Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Так, в примере выше первые два набора (1,2,5), (2,5,1) есть один и тот же результат выбора, а набор (4,4,5) — другой результат выбора.
Подсчитаем теперь, сколько возможно различных результатов при каждой из четырех схем (выбор с возвращением и без, и в каждом из этих случаев учитываем ли мы порядок или нет).
Источник
