Сколькими способами можно разместить пять различных

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

I. Сообщение темы и цели урока

II. Общая характеристика контрольной работы

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).

III. Контрольная работа в 4 вариантах

К-7. Вариант 1

Сколькими способами можно разместить пять различных книг на полке?
Сколько трехзначных чисел с разными цифрами можно составить из цифр 0, 1, 3, 6, 7, 9?
Из десяти членов команды надо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Вычислите 3Р₃ + 2А 2 ₁₀ – С 2 ₇.
Выпускники экономического института работают в трех различных компаниях: 17 человек – в банке, 23 – в фирме и 19 –в налоговой инспекции. Найдите вероятность того, что случайно встреченный выпускник работает в фирме.
Мишень представляет собой три круга (один внутри другого), радиусы которых равны 3, 7 и 8 см. Стрелок выстрелил не целясь и попал в мишень. Найдите вероятность того, что он попал в средний круг, но не попал в маленький круг.

К-7. Вариант 2

Сколькими способами можно разместить шесть различных книг на полке?
Сколько трехзначных чисел с разными цифрами можно составить из цифр 0, 3, 4, 5, 8?
Из восьми членов команды надо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Вычислите Р₄ – 2А 2 ₉ + 3С 2 ₈.
Выпускники экономического института работают в трех различных компаниях: 19 человек – в банке, 31 – в фирме и 15 –в налоговой инспекции. Найдите вероятность того, что случайно встреченный выпускник работает в банке.
Мишень представляет собой три круга (один внутри другого), радиусы которых равны 4, 5 и 9 см. Стрелок выстрелил не целясь и попал в мишень. Найдите вероятность того, что он попал в средний круг, но не попал в маленький круг.

К-7. Вариант 3

Сколько существует трехзначных чисел, в записи которых есть хотя бы одна цифра 0?
Определите число диагоналей десятиугольника.
Решите уравнение
У Кати есть 9 разных книг по математике, у Коли – 8 книг по физике. Сколькими способами они могут обменяться шестью книгами?
На пяти карточках выписаны буквы слова «гамак». Карточки перемешивают и выкладывают в ряд случайным образом. Найдите вероятность того, что получится то же самое слово.
Коля и Витя договорились встретиться в парке с 14.00 до 15.00. Пришедший первым ждет другого в течение 20 мин, после чего уходит. Какова вероятность, что они встретятся?

К-7. Вариант 4

Сколько существует четырехзначных чисел, в записи которых есть хотя бы одна цифра 0?
Определите число диагоналей двенадцатиугольника.
Решите уравнение
У Кати есть 10 разных книг по математике, у Коли – 7 книг по физике. Сколькими способами они могут обменяться пятью книгами?
На пяти карточках выписаны буквы слова «хохот». Карточки перемешивают и выкладывают в ряд случайным образом. Найдите вероятность того, что получится то же самое слово.
Коля и Витя договорились встретиться в парке с 15.00 до 16.00. Пришедший первым ждет другого в течение 30 мин, после чего уходит. Какова вероятность, что они встретятся?

IV. Подведение итогов контрольной работы

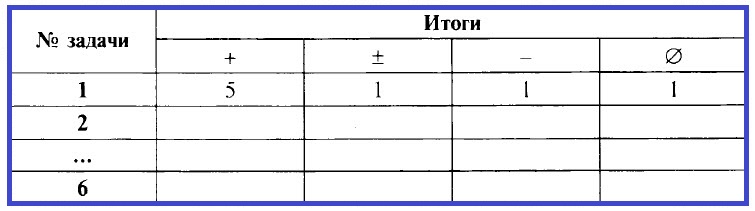
Распределение работ по вариантам и результаты решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).

Обозначения:
+ (число решивших задачу правильно или почти правильно);
± (число решивших задачу со значительными погрешностями);
– (число не решивших задачу);
∅ (число не решавших задачу).

Типичные ошибки, возникшие при решении задач.
Наиболее трудные задачи и их разбор (учителем или школьниками, решившими их).
Разбор всей контрольной работы (вывесить на стенде ответы к заданиям и разобрать наиболее трудные варианты).

V. Решение заданий ( ответы )

VI. Подведение итогов урока

Вы смотрели: Алгебра 9 Макарычев Контрольная № 7 с ответами. Поурочное планирование по алгебре для 9 класса по УМК Макарычев (Просвещение). Глава IV. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ. Урок 81. Контрольная работа по теме «Элементы комбинаторики и теории вероятностей» + ОТВЕТЫ.

Источник

Сколькими способами можно разместить пять различных

Введение в теорию множеств и комбинаторику

Практическая работа № 12. Перестановки

Вопросы к работе

Что такое « перестановки из n элементов»?
Сколько перестановок существует для n элементов?
Какие перестановки называются перестановками с повторениями?
По какой формуле вычисляется число перестановок с повторениями?

Образцы решения заданий

Пример 1.Вычислить

. Итак,

Пример 2. Сколькими способами можно рассадить на скамейке пять человек?

Решение: Способов столько, сколько различных перестановок можно составить из 5 элементов, т. е. . Итак, пять человек на скамейке можно рассадить 120 способами.

Пример 3. Сколько всех семизначных чисел, у каждого из которых цифра 6 встречается 3 раза, а цифра 5 четыре раза?

чисел.

Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами это можно сделать? (Ответ: 2520).
Сколькими способами можно упаковать девять различных книг в трех бандеролях соответственно по 2, 3, 4 книги в каждой бандероли? (Ответ: ).
Сколькими способами можно распределить семь молодых специалистов по трем цехам, которым, соответственно, нужны 1, 2, 4 специалиста? (Ответ: ).
Сколькими способами можно составить список из 25 студентов? (Ответ: ).
Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется одно письмо? (Ответ: ).
Десять лиц, которые отдельно обедают и ужинают в одной и той же столовой, просят содержателя подождать с получением денег до тех пор, пока они не пересядут за столом всеми возможными способами, если каждый день за обедом они будут сидеть по-другому. Сколько лет пришлось бы ждать содержателю столовой, если бы он согласился на это предложение? (Ответ: около 4971 года).
Сколькими способами 15 книг можно расположить на полке? (Ответ: 15!).
Сколькими способами можно переставить буквы в слове «математика»? (Ответ: ).
В доме отдыха давали на десерт либо яблоко, либо апельсин, либо мандарин. В течение 24 дней было выдано 9 яблок, 7 мандаринов и 8 апельсинов. Сколько различных вариантов выдачи может быть? (Ответ:
Сколькими способами можно переставить буквы слова «перешеек» так, чтобы 4 буквы «е» шли подряд? (Ответ: ).

Задания для самоконтроля

Найти все натуральные n , удовлетворяющие неравенству:

Источник

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Источник