Сколькими способами можно разместить n предметов по m ящикам

Комбинаторные конфигурации

Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.

Комбинаторные задачи

Для формулировки и решения комбинаторных задач используются различные модели комбинаторных конфигураций. Рассмотрим следующие две наиболее популярные.

1. Дано n предметов. Их нужно разместить по m ящикам так, чтобы выполнялись заданные ограничения. Сколькими способами это можно сделать?

2. Рассмотрим множество функций

Не ограничивая общности, можно считать, что

Сколько существует функций F, удовлетворяющих заданным ограничениям?

Большей частью соответствие конфигураций, описанных на «языке ящиков» и «языке функций», очевидно, поэтому доказательство правильности способа подсчета (вывод формулы) можно провести на любом языке. Если сведение одной модели к другой не очевидно, то оно включается в доказательство.

Размещения

Число всех функций (при отсутствии ограничений), или число всех возможных способов разместить n предметов по m ящикам, называется числом размещений и обозначается U(m,n).

Каждый из n предметов можно разместить m способами.

При игре в кости бросаются две кости и выпавшие на верхних гранях очки складываются. Какова вероятность выбросить 12 очков? Каждый возможный исход соответствует функции F:<1,2>→ <1,2,3,4,5,6>(аргумент – номер кости, результат – очки на верхней грани).

Таким образом, всего возможно U(6,2)=6 2 =36 различных исходов. Из них только один (6+6) дает двенадцать очков. Вероятность 1/36.

Размещения без повторений

Число инъективных функций, или число всех возможных способов разместить n предметов по m ящикам, не более чем по одному в ящик, называется числом размещений без повторений и обозначается A(m,n) или [m]_n, или (m)_n.

Теорема: A(m,n)=

Ящик для первого предмета можно выбрать m способами, для второго — (m-1) способами, и так далее. Таким образом,

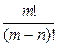A(m,n)=m*(m-1)*. *(m-n+1)=

По определению считают, что A(m,n)=0 при n>m и A(m,0)=1.

В некоторых видах спортивных соревнований исходом является определение участников, занявших первое, второе и третье места. Сколько возможно различных исходов, если в соревновании участвуют n участников? Каждый возможный исход соответствует функции F: <1,2,3>→ <1..n>(аргумент – номер призового места, результат – номер участника). Таким образом, всего возможно A(n,3)=n*(n-1)*(n-2) различных исходов.

Перестановки

Число взаимнооднозначных функций, или число перестановок n предметов, обозначается P(n).

P(n) = A(n,n) = n*(n-1)*. *(n-n+1) = n*(n-1)*. *1 = n!

Сколькими способами 6 человек могут сесть на 6 стульев?

Пронумеруем стулья числами 1,2,3,4,5,6 и обозначим человека, севшего на k-стул, через . Тогда – перестановка из имен этих 6-и людей, причем каждой такой перестановке соответствует один и только один способ размещения на стульях. Значит, число способов равно P₆=6!=720.

Пример: Секретные замки

Для запирания сейфов и автоматических камер хранения багажа применяют секретные замки, которые открываются лишь тогда, когда набрано «тайное слово» (или тайный набор цифр). Это слово набирают с помощью одного или нескольких дисков, на которых изображены буквы (или цифры). Пусть число букв на каждом диске равно 12, а число дисков равно 5. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова и подбирающим его наудачу?

Из условия задачи видно, что порядок выбираемых букв существен (одно дело набрать на первом диске букву «а», а на втором букву «б», а другое — набрать эти же буквы в обратном порядке). Поэтому мы имеем здесь дело с кортежами. При этом никаких ограничений на эти кортежи не наложено.

Так как по условию каждая буква может быть выбрана 12 способами, а длина кортежей равна 5, то получаем, что число комбинаций равно 12 5 = 248 832. Значит, неудачных попыток может быть 248 831. Считая по 10 секунд на одну попытку, получаем, что для открытия сейфа понадобится более 340 часов непрерывной работы. Впрочем, обычно сейфы делают так, чтобы после первой же неудачной попытки раздавался сигнал тревоги.

Сочетания

Число строго монотонных функций, или число размещений n неразличимых предметов по m ящикам, не более чем по одному в ящик, то есть число способов выбрать из m ящиков n ящиков с предметами, называется числом сочетаний и обозначается C(m,n) или C n _m или ( n _m).

Теорема: C(m,n)=

В начале игры в домино каждому играющему выдается 7 костей из имеющихся 28 различных костей. Сколько существует различных комбинаций костей, которые игрок может получить в начале игры? Очевидно, что искомое число равно числу 7-элементных подмножеств 28-элементного множества. Имеем:

С(28,7)=

Сочетания с повторениями

Число монотонных функций, или число размещений n неразличимых предметов по m ящикам, называется числом сочетаний с повторениями и обозначается V(m,n).

Сколькими способами можно рассадить вновь прибывших гостей среди гостей, уже сидящих за круглым столом? Очевидно, что между сидящими за круглым столом гостями имеется промежутков, в которые можно рассаживать вновь прибывших.

Источник

Сколькими способами n предметов можно произвольно разложить по k ящикам, если:

Сколькими способами предметов можно произвольно разложить по ящикам, если:

1) Все предметы и все ящики неразличимы
2) Все предметы различимы, а ящики неразличимы
3) Все предметы и все ящики различимы
4) Все предметы неразличимы, а ящики различимы

1) Корректно ли посчитать способы разместить предметы по различимым ящикам и разделить на перестановок ящиков? Вот так .
Я так понимаю этот пункт можно переформулировать как разложение натурального числа на слагаемые, но тогда не ясно как разложения, отличающиеся лишь порядком слагаемых посчитать и исключить из .

2) Первый предмет кидаем в один из k ящиков, k способами соответственно. Второй либо в способом в один из пустых ящиков, либо способами в ящик, где уже есть конверт. т.е. всего способов. И т.д. способ для каждого следующего предмета. Итого .

3) Для каждого предмета произвольно выбирается ящик, получаем способов.

4) Порядок предметов в ящике не важен, важно количество .

Сколькими способами можно разложить шары по ящикам?
Сколькими способами можно разложить 8 одинаковых шаров по 3 одинаковым ящикам?

Сколькими способами можно разложить все шары по ящикам?
Имеется 6 различных ящиков и 10 неразличимых шаров. Сколькими способами можно разложить все шары.

Сколькими способами можно разложить a одинаковых шаров по b различным ящикам?
Сколькими способами можно разложить a одинаковых шаров по b различным ящикам, так, чтобы в каждом.

Сколькими способами можно разложить 24 различных предмета по четырем разным ящикам
Сколькими способами можно разложить 24 различных предмета по четырем разным ящикам так, чтобы в.

Сколькими способами можно разложить 28 различных предметов в четыре одинаковых ящика?
Добрый день Нужна ваша помощь Сколькими способами можно разложить 28 различных предметов в.

Сколькими способами можно разложить 3 белых и 4 черных шара по 6 разным ящикам, причём ни один ящик не должен быть пуст
Сколькими способами можно разложить 3 белых и 4 черных шара по 6 различным ящикам, причём ни один.

Сколькими способами можно разместить N шаров по N ящикам
Сколькими способами можно разместить N шаров по N ящикам, включая те случаи когда несколько ящиков.

Сколькими способами можно разместить шары по ящикам без ограничений
Добрый день. Есть две задачи: 1) Есть N разных шаров и M одинаковых ящиков. Сколькими способами.

Сколькими способами можно составить раписание предметов?
Проверьте пожалуйста. В некотором классе изучают 10 различных предметов. В пятницу завуч должен.

Источник

Глава 10. Комбинаторика. Комбинаторные конфигурации

Во многих практических случаях возникает необходимость подсчитать количе­ство возможных комбинаций объектов, удовлетворяющих определенным усло­виям. Такие задачи называются Комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.

Число всех функций (при отсутствии ограничений), или число всех возможных способов разместить П Предметов по Т Ящикам называется, Числом размещений И обозначается U(M,N).

Каждый из N предметов можно разместить M способами.

При игре в кости бросаются две кости и выпавшие на верхних гранях очки скла­дываются. Какова вероятность выбросить 12 очков? Каждый возможный исход соответствует функции F: <1,2>® <1,2,3,4,5,6>(аргумент — номер кости, ре­зультат — очки на верхней грани). Таким образом, всего возможно U(6,2) = 62 = 36 различных исходов. Из них только один (6 + 6) дает двенадцать очков. Вероятность 1/36.

Размещения без повторений

Число инъективных функций, или число всех возможных способов разместить П Предметов по M ящикам, не более чем по одному в ящик, называется Числом размещений без повторений И обозначается А(M, п) или [M]n, или (M)n.

ТЕОРЕМА

Ящик для первого предмета можно выбрать M способами, для второго — M — 1 способами, и т. д. Таким образом,

По определению считают, что А(Т, N) = 0 при П > Т И А(Т, 0) = 1.

В некоторых видах спортивных соревнований исходом является определение участников, занявших первое, второе и третье места. Сколько возможно раз­личных исходов, если в соревновании участвуют П Участников? Каждый воз­можный исход соответствует функции F: <1,2,3>® <1..N> (аргумент — номер призового места, результат — номер участника). Таким образом, всего возможно А(П,3) = П(П — 1)(N — 2) различных исходов.

Число взаимнооднозначных функций, или Число перестановок п Предметов, обо­значается Р(П).

Последовательность E = (E1. Em) непустых подмножеств множества Е (E Ì 2E, Ei Ì Е, Ei ¹ Æ) называется Цепочкой В Е, Если

Цепочка E называется Полной Цепочкой в Е, Если |E| = |Е|. Сколько существует полных цепочек? Очевидно, что в полной цепочке каждое следующее подмноже­ство Ei+1 получено из предыдущего подмножества Ei Добавлением ровно одного элемента из Е И, таким образом, |E1| = 1, |E2| = 2, . |Ет| = |Е| = т. Следова­тельно, полная цепочка определяется порядком, в котором элементы Е Добавля­ются для образования очередного элемента полной цепочки. Отсюда количество полных цепочек — это количество перестановок элементов множества Е, Рав­ное M!.

Число строго монотонных функций, или число размещений П Неразличимых предметов по Т Ящикам, не более чем по одному в ящик, то есть число способов выбрать из m ящиков N ящиков с предметами, называется Числом сочетаний И обозначается С(Т, п) или или .

ТЕОРЕМА

1. Число размещений без повторений нужно разделить на число перестановок, поскольку предметы неразличимы.

2. Число сочетаний является числом строго монотонных функций, потому что строго монотонная функция F: 1..п ® L..M определяется набором своих значений, причем 1£ F(1) M.

В начале игры в домино каждому играющему выдается 7 костей из имеющихся 28 различных костей. Сколько существует различных комбинаций костей, которые игрок может получить в начале игры? Очевидно, что искомое число равно числу 7-элементных подмножеств 28-элементного множества. Имеем:

Сочетания с повторениями

Число монотонных функций, или число размещений N неразличимых предме­тов по M ящикам, называется Числом сочетаний с повторениями И обозначается V(M, N).

Сколькими способами можно рассадить N Вновь прибывших гостей среди M Го­стей, уже сидящих за круглым столом? Очевидно, что между то сидящими за круглым столом гостями имеется M Промежутков, в которые можно рассаживать вновь прибывших. Таким образом, это можно сделать

Источник

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

.

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Источник