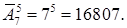12. Размещения с повторениями
Пусть выбор k элементов из некоторого множества, состоящего из n элементов, производится с возвращением и с упорядочением их в последовательную цепочку. Различными исходами такого выбора будут всевозможные наборы (вообще говоря, с повторениями) отличающиеся либо составом элементов, либо порядком их следования. Получаемые в результате комбинации называются размещениями с повторениями из n элементов по k элементов.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента: ab, ac, ba, bc, ca, cb, aa, bb, cc.
Таким образом, размещение с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое размещение с повторениями из n элементов по k элементов может состоять не только из различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Число размещений с повторениями 

Пример 10.1. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:
Пример 10.2. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?
Решение. Данная задача есть задача на отыскание числа размещений с повторениями

Пример 10.3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Решение. Число всех букв, каждая из которых записывается одним символом, равно 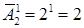
Число всех букв, каждая из которых записывается двумя символами, равно 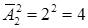
Число всех букв, каждая из которых записывается тремя символами, равно 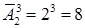
Число всех букв, каждая из которых записывается четырьмя символами, равно 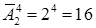
Число всех букв, каждая из которых записывается пятью символами, равно 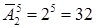
Число всех указанных букв будет равно 62.
10.1. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?
Ответ: 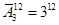
10.2. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?
Ответ: 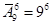
10.3. Сколькими способами можно разместить 8 пассажиров по трем вагонам?
Ответ: 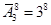
10.4. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?
Ответ: 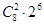
10.5. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа 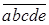
Ответ: 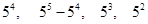
10.6. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?
Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2k k-значных числа, то общее количество искомых чисел равно 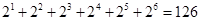
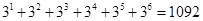
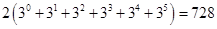
10.7. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?
Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т. е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: 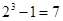
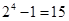
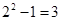
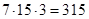
Источник
Задачи комбинаторики.

Чтобы научиться быстро бегать, нужно много бегать. Чтобы научиться хорошо решать сложные задачи, нужно решать много простых задач. И то, и другое надо делать с умом. Последовательно тренировать определенные группы мышц, и постепенно вникать в смысл математических выражений.
Давайте рассмотрим несколько очень простых задач, сравнивая их между собой. Сравнение поможет нам понять и запомнить, как выбрать нужную формулу для подсчёта числа вариантов в той или иной ситуации. А чтобы никто не усомнился в том, что задачи действительно простые, я взяла за основу Сборник тестовых заданий к учебнику Н.Я. Виленкина и др. «Математика. 5 класс». Конечно, для пятиклассников это задания высокого уровня сложности «С», но они справляются. Дело в том, что эти задачи можно решить как простым перебором вариантов, тем быстрее, чем выше уровень обобщения, так и по формулам комбинаторики. Старшеклассникам рекомендую повторить формулы и правила комбинаторики, если вы попали на эту страницу из поисковика, миновав теорию.
Итак,
— внимательно читаем условия 2-ух задач из одной строки таблицы;
— решаем обе задачи любыми доступными способами (желательно не одним);
— открываем ответы нажатием на зеленые кнопки и сравниваем их со своими ответами;
— открываем решения и комментарии к ним нажатием на желтые кнопки.
Помните, что ваше решение не обязательно должно совпадать с моим, достаточно, чтобы оно было логичным и позволяло получить верный ответ.
Задачи и решения.
| Задача 1a | Задача 1b |
|---|---|
| При окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек перешло из рук в руки, если во встрече участвовали 6 специалистов? | При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 6 друзей? |
| Задача 2a | Задача 2b |
| В хоровом кружке занимаются 9 человек. Необходимо выбрать двух солистов. Сколькими способами это можно сделать? | В спортивной команде 9 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать? |
| Два солиста равноправны. (Может быть, и петь планируют дуэтом.) Нас не волнует порядок следования в группе из 2-ух человек, выбранных из 9-ти. Значит определяем число сочетаний из 9 по 2. Казалось бы, мы снова выбираем 2-ух человек из 9-ти, но теперь между ними качественная разница. Они будут выполнять разные обязанности в команде. Мы выбираем капитана И заместителя независимо друг от друга. Поэтому применим правило умножения вариантов (И-правило). Из 9-ти человек капитана можно выбрать 9-тью способами. Его заместителя из оставшихся 8-ми человек — 8-мью способами. Общее число вариантов: 9·8 = 72. (Заметьте, что если сначала выбрать заместителя из 9 человек, а потом капитана из оставшихся 8-ми, результат будет тот же.) Можно рассуждать иначе. Есть два места для капитана и его заместителя, нужно разместить на них 2-ух человек, выбрав их из 9-ти. Такие группировки (выборки) называются размещениями. Число размещений определяем по формуле | |
| Задача 3a | Задача 3b |
| Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях? | В понедельник в пятом классе 5 уроков: музыка, математика, русский язык, литература и история. Сколько различных способов составления расписания на понедельник существует? |
| Легко понять, что в этой задаче речь идет о перестановках. 6 гостей занимают все 6 стульев и могут только меняться местами. Число перестановок из 6 определяем по формуле Может быть, не так очевидно, но это тоже перестановки. С точки зрения математики, вообще та же самая задача. Представьте себе, что расписание составляете вы. Чертите таблицу с пятью строками для пяти уроков («готовите стулья») и вписываете в каждую строку название одного из 5-ти предметов («рассаживаете гостей»). Число перестановок из 5 определяем по формуле | |
| Задача 4a | Задача 4b |
| Пятеро друзей сыграли между собой по одной партии в шахматы. Сколько всего партий было сыграно? | Сколькими способами 10 футбольных команд могут разыграть между собой золотые, бронзовые и серебряные медали? |
| В шахматной партии 2 равноправных участника (точно также, как в задаче о рукопожатиях). Значит из 5-ти человек формируем группы по 2 без учета порядка следования — сочетания. Определяем число сочетаний из 5 по 2. На пьедестале почёта находятся 3 команды из 10, и для них очень существенно, кто какое место занял, т.е. порядок следования. Составление групп с учетом порядка следования — размещения. Число размещений определяем по формуле | |
| Задача 5a | Задача 5b |
| В меню столовой предложено на выбор 2 первых блюда, 6 вторых и 4 третьих блюда. Сколько различных вариантов обеда, состоящего из первого, второго и третьего блюда, можно составить? | Имеется 6 видов овощей. Решено готовить салаты из трёх видов овощей. Сколько различных вариантов салатов можно приготовить? |
| Задача 6a | Задача 6b |
| В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими разными способами можно выбрать покупку из одного блокнота и одной ручки? | В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими способами можно выбрать покупку из двух разных блокнотов и одной ручки? |
| Выбираем одну ручку И один блокнот. Одну ручку из 4-ёх 4-мя способами, один блокнот из 7-ми — 7-ю способами. Применяем правило умножения Выбираем одну ручку И два блокнота. Снова можем применить правило умножения вариантов. Одну ручку из 4-ёх можем выбрать 4-мя способами, два блокнота из 7-ми — ? способами. | |
| Задача 7a | Задача 7b |
| На прививку в медпункт отправились 7 друзей. Сколькими разными способами они могут встать в очередь у медицинского кабинета? | Секретный замок состоит из 4 барабанов, на каждом из которых можно выбрать цифры от 0 до 9. Сколько различных вариантов выбора шифра существует? |
| Число способов встать в очередь равно числу перестановок 7-ми друзей в пределах этой очереди. Задача такая же, как о гостях и стульях, но обратите внимание, насколько быстро растет число вариантов при увеличении числа переставляемых предметов. На каждом барабане можно выбрать 1-ну цифру из 10-ти 10-тью способами и независимо от других, поэтому применяем правило умножения: Можно также считать, что нужно разместить 10 цифр на 4-ёх местах с повторениями. В комбинаторике существует раздел «Выборки с повторениями» (см. подробнее). В данном случае нам нужна формула для размещений. Число размещений с повторениями определяется как n k , где n — количество элементов для выбора (здесь n = 10 цифр), k — объём выборки или количество возможных повторов одного элемента (здесь k = 4, одна и та же цифра может быть установлена на всех четырех барабанах). Таким образом, искомое число вариантов | |
| Задача 8a | Задача 8b |
| Сколько различных трёхзначных чисел можно составить при помощи цифр 4, 7, 9? (Цифры в записи числа не повторяются). | Сколько различных трёхзначных чисел можно составить с помощью цифр 1, 3, 7? (Цифры могут повторяться). |
| Трёхзначное число состоит из 3-ёх цифр, которые нам даны. Поскольку цифры не могут повторяться, то получать различные числа можно только путем их перестановки. Число перестановок из 3-ёх определяем по формуле Если цифры могут повторяться, то по разрядам их можно размещать независимо от друг от друга. Значит можем применить правило умножения вариантов (И-правило). Одну цифру из трёх для разряда сотен можно выбрять 3-мя способами, И одну цифру из тех же трёх для разряда десятков — 3-мя способами, И одну из трёх для разряда единиц — 3-мя способами. Общее число вариантов | |
| Задача 9a | Задача 9b |
| Сколько различных трёхзначных чисел можно составить с помощью цифр 7 и 3? | Сколько различных двузначных чисел можно составить при помощи цифр 4, 7, 9? (Цифры в записи числа не повторяются). |
| Задача 10a | Задача 10b |
| Сколько нечетных трёхзначных чисел можно составить из цифр 3, 4, 8, 6? (Цифры в записи числа не могут повторяться). | Сколько различных трёхзначных чисел можно составить из цифр 7, 6, 5, 0, если цифры в записи числа не могут повторяться? |
| Искомое число должно оканчиваться цифрой 3, так как 4, 6 и 8 делятся на 2 без остатка. Поэтому позиция единиц у нас уже занята, и остается разместить 3 цифры на 2-ух позициях — десятков и сотен. Число размещений из 3 по 2 определяем по формуле Сначала определим, сколько всего можно составить групп из 4-ёх заданных цифр по 3 с учётом порядка следования и без повторений. | |
| Задача 11a | Задача 11b |
| Сколько четных трёхзначных чисел можно составить из цифр 3, 4, 5, 6? (Цифры в записи числа не могут повторяться). | Сколько четных трёхзначных чисел можно составить из цифр 3, 4, 5, 6? (Цифры в записи числа могут повторяться). |
| Четными будут числа, оканчивающиеся на 4 ИЛИ на 6. Поэтому подсчитаем количество вариантов, заканчивающихся на одну из этих цифр, а затем воспользуемся правилом сложения (ИЛИ-правилом), чтобы определить общее число вариантов. Так же, как в предыдущем случае рассмотрим отдельно числа, заканчивающиеся 4-кой и 6-кой, а затем воспользуемся правилом сложения вариантов. | |
| Задача 12a | |
| Сколько различных дробей можно составить с использованием цифр 2, 3, 4? (В числителе и знаменателе не может быть одна и та же цифра.) | |
| Заметим, что не только в числителе и знаменателе не может быть одна и та же цифра, но цифры вообще не могут повторяться, иначе задача не имела бы смысла. В число дробей входили бы, например, 2/3, 2/33, 2/333, 2/3333 и т.п. Таких вариантов бесконечное число. Если вы получили ответ 12, а не 18, обязательно разберитесь почему. Это иначе понятое условие задачи? Забыты неправильные дроби? Ошибка в комбинаторике? Комментарии.O формуле для числа сочетаний. O формуле для числа размещений. Выборки с повторениями. | |
| Перейти на главную страницу сайта. | |
 |