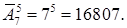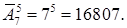Сколькими способами можно разложить 20 одинаковых канцелярских скрепок по 3 разным коробкам
Пусть имеется три элемента ( n = 3): a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента ( k = 2): ab, ac, ba, bc, ca, cb, aa, bb, cc (порядок важен!)
Общее число размещениями с повторениями определяется формулой:
Пример 1. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?
Решение. Данная задача есть задача на отыскание числа размещений с повторениями
.
Пример 2. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:
Пример 3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Решение. Число всех букв, каждая из которых записывается одним символом, равно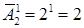 
.
Число всех букв, каждая из которых записывается двумя символами, равно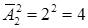 
.
Число всех букв, каждая из которых записывается тремя символами, равно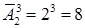 
.
Число всех букв, каждая из которых записывается четырьмя символами, равно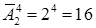 
.
Число всех букв, каждая из которых записывается пятью символами, равно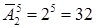 
.
Число всех указанных букв будет равно 62.
Задачи.
1. Сколькими способами можно разложить 12 различных деталей по 3 ящикам?
2. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?
Ответ: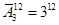 
.
3. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?
Ответ: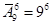 
.
4. Сколькими способами можно разместить 8 пассажиров по трем вагонам?
Ответ: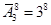 
.
5. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?
Ответ: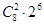 
.
6. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа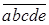 
(повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a=1; 2) a¹2; 3) a=3, b=2; 4) a=3, b=4, c=5?
Ответ: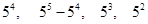 
.
7. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?
Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2k k-значных числа, то общее количество искомых чисел равно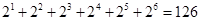 
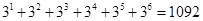
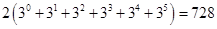
. б) Для трёх цифр аналогично получаем 
. в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим 
чисел.
8. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?
Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т. е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: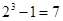 
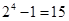
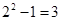
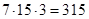
способов выбора кур. Точно так же есть 
способов выбора уток и 
способов выбора гусей. Всего 
способов.
Источник
12. Размещения с повторениями
Пусть выбор k элементов из некоторого множества, состоящего из n элементов, производится с возвращением и с упорядочением их в последовательную цепочку. Различными исходами такого выбора будут всевозможные наборы (вообще говоря, с повторениями) отличающиеся либо составом элементов, либо порядком их следования. Получаемые в результате комбинации называются размещениями с повторениями из n элементов по k элементов.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента: ab, ac, ba, bc, ca, cb, aa, bb, cc.
Таким образом, размещение с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое размещение с повторениями из n элементов по k элементов может состоять не только из различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Число размещений с повторениями 
можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т. д. По принципу умножения находим
. (10.1)
Пример 10.1. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:
Пример 10.2. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?
Решение. Данная задача есть задача на отыскание числа размещений с повторениями
.
Пример 10.3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Решение. Число всех букв, каждая из которых записывается одним символом, равно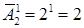 
.
Число всех букв, каждая из которых записывается двумя символами, равно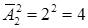 
.
Число всех букв, каждая из которых записывается тремя символами, равно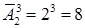 
.
Число всех букв, каждая из которых записывается четырьмя символами, равно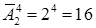 
.
Число всех букв, каждая из которых записывается пятью символами, равно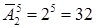 
.
Число всех указанных букв будет равно 62.
10.1. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?
Ответ: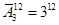 
.
10.2. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?
Ответ: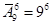 
.
10.3. Сколькими способами можно разместить 8 пассажиров по трем вагонам?
Ответ: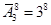 
.
10.4. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?
Ответ: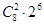 
.
10.5. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа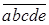 
(повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a=1; 2) a¹2; 3) a=3, b=2; 4) a=3, b=4, c=5?
Ответ: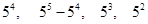 
.
10.6. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?
Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2k k-значных числа, то общее количество искомых чисел равно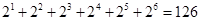 
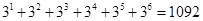
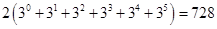
. б) Для трёх цифр аналогично получаем 
. в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим 
чисел.
10.7. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?
Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т. е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: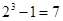 
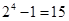
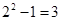
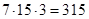
способов выбора кур. Точно так же есть 
способов выбора уток и 
способов выбора гусей. Всего 
способов.
Источник
Сколькими способами можно разложить 20 одинаковых предметов по 5 различимым ящикам так, чтобы а) оказалось не более двух пустых ящиков; б) в каждом ящ
Сколькими способами можно разложить a одинаковых шаров по b различным ящикам?
Сколькими способами можно разложить a одинаковых шаров по b различным ящикам, так, чтобы в каждом.
Сколькими способами можно разложить шары по ящикам?
Сколькими способами можно разложить 8 одинаковых шаров по 3 одинаковым ящикам?
Сколькими способами можно разложить все шары по ящикам?
Имеется 6 различных ящиков и 10 неразличимых шаров. Сколькими способами можно разложить все шары.
Сколькими способами можно разложить 30 шаров в 8 различных ящиков?
Сколькими способами можно разложить 30 шаров в 8 различных ящиков, чтобы: 1)В каждом ящике было не.
Данная задача решается следующим образом.
Берем вектор с 24-мя координатами, который будет заполнен 20-ю нулями и 4-мя единицами.
Нули соответствуют нашим одинаковым предметам, а место расположения единиц будет соответствовать «перегородкам» между ящиками.
Тоесть: набор (000100100000100000000001) что в первом ящике лежит три предмета (первые три нуля до первой единицы), во втором два предмета (два нуля до второй единицы), затем 5 предметов, затем 10 предметов, в последнем ни одного, потому что после последней едицы нет нулей.
Теперь легко посчитать, что всего способов разбить преметы (все возможные) равно С из 24 по 4, т.е. 24!/(20!4!)=24*23*22*21/(1*2*3*4)=21*22*23=10626.
Второй пункт решается так: чтобы в каждом ящике было как минимум два предмета, это значит что в каждом «блоке» нулей в векторе должно быть хотя бы два нуля. «Вычеркнем» их, таким образом уменьшив размерность вектора до 14 координат. Теперь заполним этот вектор 4-мя единицами и 10-ю нулями. Всего способов С из 14 по 4, т.е. 14*13*12*11/(1*2*3*4)=11*13*7=1001. Этот «маневр» дает нам необходимы ответ на второй пункт. Действительно, в каждом таком 14-ти мерном векторе «блоки» нулей соответствуют количесву предметов. Например (10010110000000) значит что лежит 0,2, 1, 0, 7 предметов в 5-ти ящиках, это одозначно соответствует набору (0+2, 2+2, 1+2, 0+2, 7+2).
Над первым пунктом я еще немного подумаю, но его надо решать помоему методом включения-исключения.
Добавлено через 9 минут
***Первый пункт решается так: есть 5 вариантов, когда пустых по 4 ящика (тоесть в одном из 5 все 20 предметов). пустые три ящика, тогда С из 5 по 2 выбираем те два ящика, которые не пустые, тоесть 10 способов, затем умножим на количество варинтов распределения предметов между ними, а именно 19 (в одном из них n предметов, вдругом 20-n, nє<1,2,3,4. 19>.тоесть всего 10*19=190 вариантов. Таким образом условие не более двух пустых ящиков равносильно пустых не три и не четыре, тоесть искомый ответ данного пункта 10626-190=10436
Добавлено через 53 секунды
как оказалось это не метод-включения-выключения, а мы просто рассмотрели событие, которое дополняет данное до единицы))))
Источник
