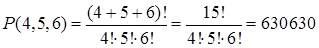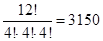Сколькими способами можно разделить 12 различных учебников между 4 студентами

Сколькими способами можно распределить 12 разных книг между четырьмя учащимися если можно, подробное объяснение?

Алгебра | 10 — 11 классы

Сколькими способами можно распределить 12 разных книг между четырьмя учащимися если можно, подробное объяснение.

На мой взгляд, тут важен и порядок элемента и сам выбор элемента, т.

Е. это сводится к размещению.

Но вычисляя по этой формуле, ответ не тот.

Тут будем использовать комбинаторику размещения.

Книги разные, поэтому разница будет если их мы меняем между учащимися.

A(m — вверху, n — снизу) = n!

\ 8! (сокращаем) = 9 х 10 х 11 х 12 = 11880.

1. В классе 30 учащихся?

1. В классе 30 учащихся.

Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории, литературе, русскому и английскому языкам?

2. В библиотеке Кате предложили на выбор из новых поступлений 10 книг и 4 журнала.

Сколькими способами она может выбрать из них 3 книги и 2 журнала?

3. Сколькими способами 8 учащихся могут встать в очередь в школьном буфете?

Число размещений 5 элементов по 3 равно?

Число размещений 5 элементов по 3 равно.

Число размещений из n элементов по четыре в 14 раз больше числа размещений из n — 2 элементов по три?

Число размещений из n элементов по четыре в 14 раз больше числа размещений из n — 2 элементов по три.

Даны элементы a, b, c, d?

Даны элементы a, b, c, d.

Из этих элементов составить группы перестановок.

Вычислите их количество.

Помогите пожалуйста ?

Сколькими способами можно расположить 17 книг на двух полках, если на одной полке можно разместить 7 книг , а на второй 10 , и порядок расположения книг на полках важен.

Из восьми учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде , Сколькими способами это можно сделать выбор?

Из восьми учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде , Сколькими способами это можно сделать выбор?

Ребят можно по подробней (максимально).

Из 8 книг и 5 журналов необходимо выбрать 3 книги и 2 журнала ?

Из 8 книг и 5 журналов необходимо выбрать 3 книги и 2 журнала .

Сколькими способами это можно сделать этот выбор?

Сколькими способами 6 человек смогут разместиться на 6 местах зрительного зала?

Сколькими способами 6 человек смогут разместиться на 6 местах зрительного зала?

Тема : «Элементы комбинаторики».

Просьба отвечать пользователей, хорошо разбирающихся в алгебре.

Пожалуйста, напишите подробное решение или объяснение, чтобы понять.

Сколькими способами можно распредилить 12 различных книг можно чертырьмя учащимися?

Сколькими способами можно распредилить 12 различных книг можно чертырьмя учащимися?

На полке стоит 12 разных книг?

На полке стоит 12 разных книг.

Сколькими способами из них можно выбрать 9 книг?

На этой странице сайта, в категории Алгебра размещен ответ на вопрос Сколькими способами можно распределить 12 разных книг между четырьмя учащимися если можно, подробное объяснение?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Источник

Как найти число перестановок с повторениями

Число перестановок c повторениями обозначают

Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы $n$. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом $k_1!$ способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют $k_2!$ перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом $ k_1!*k_2!*. *k_m! $ способами так, что она остаётся неизменной.

Число различных перестановок с повторениями, которые можно составить из данных элементов, равно

Пример 1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?

Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем

Калькулятор длч вычисления числа перестановок с повторениями

Пример 2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?

Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:

.

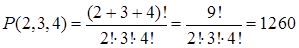
Пример 3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?

Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем

.

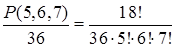
Пример 4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?

Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим

.

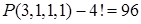
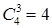
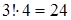
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить способами. Всего получаем способа.

1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?

Ответ: .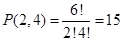

2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?

Ответ: .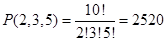

3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?

Ответ: .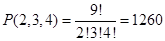

4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?

Ответ: .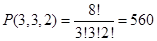

5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?

Ответ: .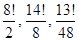

6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?

Ответ: .

7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?

Ответ: .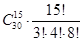

8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?

Ответ: .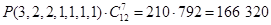

9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?

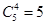
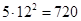
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать способами. Всего способов.

Источник

Сколькими способами можно разделить 12 различных учебников между 4 студентами

Вопрос по математике:

Сколькими способами можно разделить 12 учебников между четырьмя студентами

Ответы и объяснения 1

Общее число способов вычисляется по формуле:

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник

Разделить 12 предметов на 4 человека

Пусть есть 12 предметов, к примеру книг.
нужно разделить их на 4 человека. При этом человеку может ничего не достаться и может достаться все, т.е возможен вариант
0-0-0-12

сколькими способами можно так разделить?
и решение пож

сам только перебирать додумался, но что-то слишком много выходит.
вроде ни к размещению, ни к сочетанию не относиться, не знаю

Как разделить набор предметов поровну
2 друга собрались в поход,собрали и взвесили все вещи. Как им разделить набор предметов.

Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок
Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок? Я нашла формулу для.

Известна масса каждого из 12 предметов, определить общую массу всего набора предметов
известна масса каждого из 12 предметов определить общую массу всего набора предметов ?

Известна масса каждого из 12 предметов. Определить общую массу всего набора предметов
Известна масса каждого из 12 предметов. Определить общую массу всего набора предметов.

Решение

это классическая задача расположения 12 шариков по 4 ящикам при том, что и то, и другое различимо (судя по условию — люди точно разные. Ну раз книги — значит, тоже).

Получается. у нас 4 человека.
Каждый объект (книга) у нас может случайно «выбрать» любого человека. Перенумеруйте мысленно людей и присвойте книгам номера, кому они достались.
Получатся варианты типа:
111111111111 (все книги достались первому человеку)
.
123243344421
.
444444444444 (все книги достались последнему человеку)

Поэтому как посчитать общее число вариантов:
4 варианта, кому может достаться 1-я книга, 4 — кому вторая и т.д.. Получается общее число вариантов — число размещений с повторением: А₄ 12 =4 12

Добавлено через 15 часов 29 минут

только число размещений с повторением обычно обозначается А с крышечкой:

Источник

Задачи по комбинаторике для 11 класса

На книжной полке стоит 20 книг по геометрии, 12 — по теории вероятностей, 7 — по дифференциальным уравнениям и 25 по истории. Сколькими способами можно выбрать книгу по математике?

Сколько трехзначных чисел можно составить из цифр 2, 4, 6, если цифры в числе не повторяются?

В магазине имеются 6 сортов шоколадных конфет и 4 сорта карамели. Сколько различных покупок конфет одного сорта можно сделать в этом магазине?

Имеется 8 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет спортлото или автомотолотереи?

Сколько можно получить различных четырехзначных чисел, вставляя пропущенные цифры в число «*3*4»?

У одного студента имеется 7 книг по математике, а другого — 10. Сколькими способами они могут осуществить обмен?

Сколько различных трехбуквенных слов можно составить из букв слова ромб?

У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имет равно 300, а ребенку дают не более трех разных имен?

Имеется 8 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну на правую руку так, чтобы эти перчатки были различных размеров?

Лесник должен посадить 5 видов деревьев по двум лесополосам. Сколькими способами лесник может посадить деревья?

Даны натуральные числа от 1 до 30. Сколькими способами можно выбрать три числа так, чтобы их сумма была четной?

Сколькими способами можно разделить 12 различных учебников между 4 студентами.

Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, испанского на любой другой из этих пяти языков?

Сколькими способами 8 человек могут встать в очередь друг за другом?

Из полного набора шахмат вынули 4 фигуры или пешки. Во скольких случаях среди них окажется: а) два коня, б) не менее двух коней?

5 юношей и 3 девушки играют в городки. Сколькими способами они могут разбиться на 2 команды по 4 человека, если в каждой команде должно быть хотя бы по одному юноше?

Сколько ожерелий из 6 бусинок каждое можно составить из 6 бусинок разного цвета?

Учащемуся необходимо сдать 4 экзамена на протяжении 8 дней. Сколькими способами это можно сделать?

Сколькими способами в отделе из 8 человек можно выбрать 3 для поощрения?

Из группы в 25 человек должны быть выделены староста и 4 члена студкома. Сколькими способами это можно сделать?

Флаги многих государств представляют собой полотнища, состоящие из трех горизонтальных полос различного цвета. Сколько таких трехцветных флагов можно составить, имея в распоряжении материал 6 цветов?

Сколькими способами можно разложить 15 одинаковых мячей в 4 разные коробки?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 801 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 283 человека из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1287904

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

Минпросвещения работает над единым подходом к профилактике девиантного поведения детей

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник