Сколькими способами можно разбить числа

комбинаторика — Разбить число

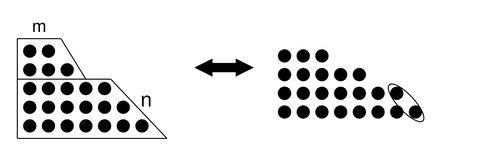
Имеются 11 точек, расположенных в ряд. Сколькими способами можно расставить между ними 3 черточки? Решение: Поставим между точками цифры .0.1.2.3.4.5.6.7.8.9. Поставив три черточки, мы отмечаем трехзначное число, цифры которого идут в возрастающем порядке, количество таких чисел равно(1098) / (123)=120. Ответ к задаче: 120 разбиений. Аналогичная задача Сколькими способами можно разбить число 11 на (k+1) слагаемых (где k=0,1,2. 9)? Указание: Ответ нужно записать так же,как и в предыдущей задаче.

задан 14 Мар ’14 18:39

1 ответ

В задаче про три чёрточки я бы рассуждал проще: есть 10 мест, и мы выбираем из них 3 для расположения чёрточек. Это сразу даёт ответ $%C_<10>^3$%, то есть $%10\cdot9\cdot8/3!$%, просто по определению. Задача о числах с возрастающими цифрами сама по себе более сложна, хотя к этому сводится. Надо ещё заметить, что тут лучше говорить не о трёхзначных числах, а о трёхразрядных. Скажем, 047 — это двузначное число, записанное как трёхразрядное.

Теперь по поводу задачи с разбиением числа 11 на слагаемые. Из того, что было сказано, я понял, что порядок слагаемых учитывается, то есть 6+5 и 5+6 считаются разными способами. В этом случае задача решается просто, и она аналогична задаче с чёрточками в следующем смысле. Пусть имеется 11 палочек (вместо точек), и между ними ставятся знаки + вместо чёрточек. Тогда, если мы ставим три «плюсика», число 11 разбивается при этом на 4 слагаемых. Например, записи |||+|+||||||+| соответствует выражение 3+1+6+1. Из сказанного следует, что разбить число $%11$% на $%k+1$% слагаемое можно $%C_<10>^k$% способами. После этого остаётся просуммировать сочетания подобно тому, как это было в одной из предыдущих задач. Здесь также надо опираться на то, что сумма всех сочетаний (по $%k$% от $%0$% до $%10$%) равна $%2^<10>$%. Поскольку случай $%k=10$% не входит, из указанного количества вычитается единица.

Источник

Нахождение количества разбиений числа на слагаемые

Содержание

Алгоритм за O(N 3 ) [ править ]

Пусть [math]P(n, m, k)[/math] — количество разбиений числа [math]n[/math] на [math]m[/math] слагаемых, каждое из которых не превосходит [math]k[/math] . Имеет место следующее рекуррентное соотношение:

[math]P(n, m, k) = \left \<\beginP(n, m, k — 1) + P(n — k, m — 1, k), & 0 \lt m \leqslant n, 0 \lt k \leqslant n \\ P(n, m, n), & k \gt n \\ 1, & n = 0, m = 0 \\ 0, & \text \end \right. [/math]

Рассмотрим множество разбиений числа [math]n[/math] на [math]m[/math] слагаемых, каждое из которых не больше [math]k[/math] . Разделим его на две непересекающиеся группы — в первой будут все разбиения, которые не содержат в качестве старшего слагаемого [math]k[/math] . Таких разбиений [math]P(n, m, k — 1)[/math] . Во второй — все разбиения со старшим слагаемым [math]k[/math] . Их столько же, сколько разбиений числа [math]n — k[/math] на [math]m — 1[/math] слагаемое, каждое из которых не больше [math]k[/math] , то есть [math]P(n — k, m — 1, k)[/math] .

Количество всех разбиений числа равно [math]\sum\limits_^nP(n, i, n)[/math] . Реализация данного алгоритма методом динамического программирования с меморизацией будет иметь асимптотику [math]O(n^<3>)[/math] .

Алгоритм за O(N 2 ) [ править ]

[math]P(n,k) = \left \< \begin P(n,k — 1) + P(n — k, k), & 0 \lt k \leqslant n \\ P(n, n), & k \gt n \\ 1, & n = 0, k = 0 \\ 0, & n \neq 0 , k = 0 \end \right.[/math]

Заметим, что нам не нужно считать количество слагаемых [math]m[/math] в разбиении. Достаточно посчитать [math]P(n, k)[/math] — количество разбиений числа [math]n[/math] на произвольное количество слагаемых, каждое из которых не больше [math]k[/math] . Рассмотрим множество таких разбиений. Разделим его на две непересекающиеся группы. В первую войдут те разбиения, в которых отсутствует слагаемое [math]k[/math] . Очевидно, таких разбиений [math]P(n, k — 1)[/math] . Во второй группе — те разбиения, в которые слагаемое [math]k[/math] вошло. Их количество совпадает с количеством разбиений числа [math]n — k[/math] на слагаемые, каждое из которых не превосходит [math]k[/math] , и равно [math]P(n — k, k)[/math] .

Количество всех разбиений числа [math]n[/math] равно [math]P(n,n)[/math] . Асимптотика [math]O(n^<2>)[/math] .

Алгоритм за O(N 3/2 ) [ править ]

Рассмотрим алгоритм нахождения количества разбиений числа [math]n[/math] на слагаемые, который работает за [math] O(n \sqrt) [/math] .

Итак, обозначим количество таких разбиений за [math] p(n) [/math] .

Рассмотрим следующее бесконечное произведение:

[math] (1 + x + x^2 + \dots)(1 + x^2 + x^4 + \dots) \dots (1 + x^k + x^ <2k>+ \dots) \dots [/math]

После раскрытия скобок каждый член произведения получается в результате умножения мономов (одночленов), взятых по одному из каждой скобки. Если в первой скобке взять [math]x^[/math] , во второй — [math]x^<2m_2>[/math] и т.д., то их произведение будет равно [math]x^.[/math] Значит, после раскрытия скобок получится сумма мономов вида [math]x^[/math] .

Можно увидеть, что [math] x^n [/math] встретится в полученной бесконечной сумме столько раз, сколькими способами можно представить [math]n[/math] как сумму [math]m_1 + 2m_2 + 3m_3 + . [/math] Каждому такому представлению отвечает разбиение числа [math]n[/math] на [math]m_1[/math] единиц, [math]m_2[/math] двоек и т.д. Таким образом, очевидно, получаются все разбиения, так как из первой скобки мы можем взять любое [math]x^[/math] , где [math]m_i \in [0 \dots \infty),[/math] то есть произвольное количество единиц в нашем разбиении. Аналогично, мы можем взять произвольное количество двоек и т.д. Но при раскрытии скобок мы находим произведения всех возможных комбинации множителей из разных скобок. Поэтому коэффициент при [math]x^n[/math] равен числу разбиений [math]p(n)[/math] .

Посмотрим теперь на выражения в скобках. Каждое из них — бесконечная геометрическая прогрессия. Полагая [math]0 \leqslant x \lt 1[/math] , по формуле ее суммирования:

[math]1 + x + x^2 + x^3 + \dots = \frac<1><1 - x>[/math] , [math]1 + x^2 + x^4 + x^6 + \dots = \frac<1><1-x^2>[/math] [math]\dots[/math] [math]1 + x^k + x^ <2k>+ x^ <3k>+ \dots = \frac<1><1-x^k>[/math] [math]\dots[/math]

Запишем теперь производящую функцию последовательности [math]p(n)[/math] :

[math]p(0) + p(1) x + p(2) x^2 + p(3) x^3 + \dots = \frac<1><(1-x)(1-x^2)(1-x^3)\dots>[/math] [math](1)[/math]

Рассмотрим произведение [math](1-x)(1-x^2)(1-x^3). [/math] , т.е. знаменатель правой части формулы [math](1)[/math] . Раскрывая в нём скобки, получим следующий результат:

[math](1 — x)(1 — x^2)(1 — x^3) . = 1 — x — x^2 + x^5 + x^7 — x^ <12>— x^ <15>+ x^ <22>+ x^ <26>— x^ <35>— x^ <40>+ . [/math]

Показатели степеней в правой части — пятиугольные числа [2] , т.е. числа вида [math](3q^2 \pm q)/2[/math] , а знаки при соответствующих мономах равны [math](-1)^q[/math] . Исходя из этого наблюдения, Эйлер предположил, что должна быть верна следующая теорема, впоследствии названная его именем.

Теорема (Пентагональная теорема Эйлера):

Доказательство:

[math]\triangleright[/math]

Раскроем в этом произведении первые [math]22[/math] скобки. Мы получим выражение где в квадратной скобке точками обозначены слагаемые, содержащие [math]x[/math] в более высокой степени, чем [math]22[/math] . Не будем выписывать эти члены, так как после умножения квадратной скобки на [math]1-x^<23>[/math] , [math]1-x^<24>[/math] и т.д. они изменятся. Выписанные же члены больше меняться не будут. Поэтому, если раскрыть все скобки, то получится бесконечный ряд, первые члены которого имеют вид Анализируя этот ряд, Эйлер пришел к выводу, что, если превратить бесконечное произведение в ряд, то в этом ряду отличны от нуля лишь слагаемые, вида [math](-1)^q x^<\frac<3q^2+q><2>>[/math] , где [math]q[/math] — натуральное число. При раскрытии скобок в исходном произведении слагаемое [math]\pm x^N[/math] встретится столько раз, сколькими способами можно разбить число [math]N[/math] на различные слагаемые. При этом, если число слагаемых четно, то появляется [math]x^N[/math] , а если это число нечетно, то появляется [math]-x^N[/math] . Например, разбиению [math]12=5+4+2+1[/math] соответствует слагаемое [math](-x^5)(-x^4)(-x^2)(-x^1)=x^<12>,[/math] а разбиению [math]12=5+4+3[/math] — слагаемое [math](-x^5)(-x^4)(-x^3)=-x^<12>[/math] . Таким образом, коэффициент при [math]x^N[/math] в разложении [math]A[/math] в ряд равен разности между количеством разбиений [math]N[/math] на четное число различных слагаемых и количеством разбиений [math]N[/math] на нечетное число различных слагаемых. Тогда теорему можно переформулировать следующим образом: Иными словами, если [math]q[/math] четно, то на одно больше разбиений на четное число слагаемых, а если [math]q[/math] нечетно, то на одно больше разбиений на нечетное число слагаемых. Докажем эту теорему с помощью диаграмм Юнга [3] . Покажем несколько способов превращения диаграммы с четным числом строк диаграмму из стольких же точек с нечетным числом строк и обратно. Так как мы рассматриваем лишь разбиения на различные слагаемые, то диаграммы таких разбиений состоят из нескольких трапеций, поставленных друг на друга. Обозначим число точек в верхней строке диаграммы через [math]m[/math] , а число строк нижней трапеции через [math]n[/math] (на рис. 1 слева изображена диаграмма, для которой [math]m=2[/math] , [math]n=3[/math] ). Преобразование 1. Предположим, что диаграмма содержит не менее двух трапеций, причем [math]m \leqslant n[/math] . В этом случае отбросим первую строку из [math]m[/math] точек, но удлиним последние [math]m[/math] строк нижней трапеции на одну точку (рис. 1). После этого общее число точек не изменится, все строки окажутся различной длины, но четность числа строк изменится. Точно такое же преобразование можно сделать, если диаграмма состоит из одной трапеции, но [math]n \geqslant m+1[/math] . Стираем верхнюю строку и к нижним [math]n-1[/math] строчкам приписываем [math]m[/math] точек. Преобразование 2.Пусть теперь диаграмма опять содержит не менее двух трапеций, но [math]m \gt n[/math] . Тогда от каждой строки последней трапеции возьмем по одной точке и составим из них первую строку (из [math] n [/math] точек) новой диаграммы. Это можно сделать, так как [math]m \gt n[/math] , и поэтому составленная строка короче первой строки исходной диаграммы. Кроме того, так как мы взяли все строки будут иметь различную длину. Наконец, новая диаграмма содержит столько же точек, что и исходная, но четность числа строк изменилась — новая диаграмма содержит еще одну строку. Преобразование 2 допускают и диаграммы, состоящие из одной трапеции, если [math]n \leqslant m — 2[/math] (появляющаяся первая строка состоит из [math]n[/math] точек, она должна быть короче бывшей первой строки, уменьшившейся до [math]m-1[/math] точки). Легко видеть, что описанные преобразования взаимно обратны — если сначала сделать одно из них, а потом второе, то снова получим исходную диаграмму. Кроме того, для каждой диаграммы может быть допустимо лишь одно из этих преобразований. Таким образом, диаграммы разбиений числа [math]N[/math] , допускающие одно из этих преобразований, распадаются на пары диаграмм с четным и нечетным числом строк, поэтому их одинаковое число. Осталось выяснить, какие же диаграммы не допускают ни одного из описанных преобразований. Ясно, что эти диаграммы состоят из одной трапеции, причем для них либо [math]m=n[/math] , либо [math]m=n+1[/math] . В первом случае диаграмма содержит точек, а во втором — на [math]n[/math] точек больше, т.е. [math]\frac<3n^2+n><2>[/math] . Приведенные рассуждения показывают, что если [math]N[/math] не является числом вида [math]\frac<3n^2 \pm n><2>[/math] , то оно имеет поровну разбиений на четное и нечетное число различных слагаемых. Очевидно также, что равенства [math]N=\frac<3n^2+n><2>[/math] и [math]N=\frac<3l^2-l><2>[/math] одновременно выполняться не могут, поэтому если [math]N=\frac<3n^2\pm n><2>[/math] , то без пары останется ровно одна диаграмма, не допускающая преобразования и имеющая [math]n[/math] строк (слагаемых [math]N[/math] ). Если [math]n[/math] — четное число, то разбиений на четное число слагаемых окажется на [math]1[/math] больше, чем на нечетное число слагаемых. Если же [math]n[/math] — нечетное число, то на [math]1[/math] больше будет разбиений на нечетное число слагаемых. Теорема доказана. Теорема (Переформулировка пентагональной теоремы): [math]\triangleleft[/math] Умножим обе части равенства [math](1)[/math] на [math]\prod\limits_^\infty \left(1-x^k \right) [/math] и воспользуемся пентагональной теоремой: [math] ( p(0) + p(1) x + p(2) x^2 + \dots)(1 — x — x^2 + x^5 + x^7 — x^ <12>— x^ <15>+ \dots) = 1 [/math] [math](2)[/math] Начнем раскрывать скобки, для наглядности мономы с одинаковыми степенями [math]x[/math] пишем друг под другом: [math] p(0) + p(1)x + p(2) x^2 + p(3) x^3 + p(4) x^4 + p(5) x^5 + p(6) x^6 + \dots [/math] [math] — p(0)x — p(1) x^2 — p(2) x^3 — p(3) x^4 — p(4) x^5 — p(5) x^6 — \dots [/math] [math] — p(0) x^2 — p(1) x^3 — p(2) x^4 — p(3) x^5 — p(4) x^6 — \dots [/math] [math]+ p(0) x^5 + p(1) x^6 + \dots [/math] Так как [math]p(0) = 1[/math] , то оно сокращается с единицей справа. Так что, чтобы выражение [math](2)[/math] было удовлетворено при любом [math]x[/math] , все коэффициенты должны быть равны [math]0[/math] . Поэтому: [math] p(1) = p(0) [/math] [math] p(2) = p(1) + p(0) [/math] [math] p(3) = p(2) + p(1) [/math] [math] p(4) = p(3) + p(2) [/math] [math] p(5) = p(4) + p(3) — p(0) [/math] [math]. [/math] Получаем формулу Эйлера, позволяющую последовательно находить числа [math]p(n)[/math] : [math] p(n) = p(n-1) + p(n-2)+ . + (-1)^ (p\left(n — \frac<3q^2 - q><2>\right) + p\left(n — \frac<3q^2 + q><2>\right)) [/math] . Асимптотика [math] O(n \sqrt) [/math] получается следующим образом. Так как [math] n — \frac<3q^2 + q> <2>\geqslant 0 [/math] , то получаем [math] q [/math] порядка [math] \sqrt [/math] , а так как находим [math]n[/math] -е число, то получаем [math] O(n \sqrt) [/math] . Источник Читайте также:  Способы соединения пластмассовых труб виды соединений Оцените статью Вам также может понравиться Ясень семена способ распространения Ясень обыкновенный Fraxinus excelsior – так в ботанической Ярлыки способы создания ярлыков ос windows Создаем ярлыки на рабочем столе Windows Создаем ярлыки Японское удобрение фуджима способ применения Удобрения Фуджима Знаете потрясающее удобрение, палочка Японский чай способ заварки Технология заваривания японского чая Известно, что Правообладателям Политика конфиденциальности Контакты