Лабораторная работа № 2.
Тема: Элементы комбинаторики. Дополнительные методы и приемы.
Цель: изучение средств пакета MS Excel для реализации возможности вычислений по основным формулам комбинаторики (сочетания, размещения, перестановки).
1. Полиномиальные коэффициенты.
Пусть дано множество 
. Построим из него кортеж состава 
в котором элемент 
встречается 
, элемент 
— 
раз и т.д. элемент 
используется 
раз. Порядок элементов в составном кортеже существенен, но перестановка местами разных копий одного и того же элемента 
на кортеж не влияет, т.е. копии одного и того же элемента считаются неотличимыми. Общее количество использованных элементов равно 
. Такие кортежи называются перестановками с повторениями. Их количество вычисляется по формуле 
.
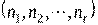
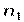
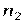
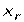
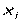
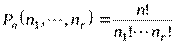
Пример. Сколькими способами можно расставить белые фигуры: 2 ладьи, 2 слона, 2 коня, ферзь и король на первой линии шахматной доски?
Решение. Рассматриваемые кортежи имеют длину 8 и состоят из элементов пяти видов. Состав кортежей имеет вид (2, 2, 2, 1, 1). Следовательно, число способов, которыми можно расставить 8 фигур на первой линии шахматной доски, равно
.
Данную задачу удобно понять в рамках стандартной урновой схемы: Имеется 8 различных шаров (позиций горизонтали) и 5 урн(классов фигур). Сколько способов распределить 8 различных шаров по 5 урнам так, что в первую урну(ладьи) попадает 2 шара, вторую(слоны) – также 2 и т.д. формируя распределение шаров по урнам вида (2,2,2,1,1). Наиболее точно данная комбинаторная задача специфицируется путем использования понятия функции. Искомое число это количество отображений следующего вида: 
Пример. Число различных слов, которое получим, переставляя буквы слова «математика», равно 
, так как мы распределяем 10 различных позиций слова между классами букв :‘м’, ’а, ’т’ и т.д.
2. Сочетания с повторениями.
Если порядок различных элементов в составном кортеже не важен, а имеет место только состав кортежа 
, то получаем неупорядоченные кортежи с повторениями или сочетания с повторениями. Таких сочетаний имеется 
Пример. В цветочном магазине продаются цветы шести сортов. Сколько можно составить различных букетов из десяти цветов в каждом? (Букеты, отличающиеся лишь расположением цветов, считаются одинаковыми.)
Решение. Рассматриваемое множество состоит из шести различных элементов, а кортежи имеют длину 10. Поскольку порядок расположения цветов в букете не играет роли, то число букетов равно числу сочетаний с повторениями из шести элементов по десяти в каждом. Следовательно, можно составить 
= 3003 различных букетов.
Пример. Сколько решений имеет уравнение
где каждое 
— неотрицательное целое число?
Решение. Решить уравнение 
равносильно задаче сформировать букет из 25 цветков используя цветки 5 типов 1-5 в некоторых неотрицательных количествах 
. Поэтому иско-мое количество решений данного уравнения — это количество раз-личных сочетаний из 5 элементов по 25 с повторениями. Итак, существуют
различных решений уравнения .
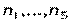
Источник
Расстановка фигур на доске
О чем эта статья:
Шахматная доска состоит из 64 клеток: 32 из них белые и 32 черные. В начале партии в распоряжении у каждого игрока его армия — король, ферзь, два слона, два коня, две ладьи и восемь пешек. Играющий белыми расставляет свои фигуры на первый и второй ряд доски, играющий черными — на седьмой и восьмой.
На диаграмме ниже — правильное расположение шахматных фигур на доске в начале игры.
Как расставить шахматы на доске
В углу армии (на клетках а1 и h1 у белых, a8 и h8 у черных) стоят сторожевые башни — ладьи. В русском языке слово «ладья» связано со словом «лодка» и обозначает боевой корабль. А вот в восточных странах ладью называли «рух» по названию хищной птицы (кстати, в английском языке ладья до сих пор называется rook). Изображение ладьи на диаграммах похоже на башню с крепостной стеной ♖.
Сбоку от ладей находится шахматный зоопарк, в котором живут кони и слоны. Кони в начале игры стоят на соседней клетке с ладьями (b1 и g1 у белых, b8 и g8 у черных). Шахматного коня ни с кем не спутать — его изображение действительно очень похоже на коня: ♘ . В английском языке конь обозначается словом knight, что переводится как «рыцарь». И правда, раньше эту фигуру часто изображали в виде рыцаря, сидящего верхом на коне.
Рядом с конями, ближе к центру первого и восьмого ряда (с1 и f1 у белых, c8 и f8 у черных), живут шахматные слоны. Шахматы были придуманы в Индии, поэтому неудивительно, что одна из фигур получила такое название — слоны в Индии являются священными животными, которые спокойно ходят по улицам индийских городов. В первых шахматах, подобно коню, эта фигура имела вид всадника, сидящего верхом на слоне. Когда игра пришла в Европу, от слона остался один всадник — у современного шахматного слона нет ни хобота, ни ушей, но название «слон» по традиции осталось. На Руси слона часто называют «офицер», и действительно, у изображения слона на диаграммах обычно рисуют крестик, похожий на орден: ♗ . Но на самом деле этот крестик связан с английским языком: в англоязычных странах слона называют bishop, что переводится как «священник». У слонов в начальной расстановке шахмат на доске особо важное место — они стоят рядом с королем и ферзем (королевой).
Ну и наконец, в самом центре шахматной армии стоят главные фигуры — король и ферзь. Король — самая главная фигура в шахматах, изображается в виде короны монарха ♔ . Ферзь — самая сильная фигура, главный советник короля. До сих пор у нас ферзя часто называют королевой — изображается он в виде элегантной женской короны ♕ . А в английском языке эта фигура так и называется queen — «королева». Начинающие шахматисты иногда путают, где на шахматной доске стоит король, а где — ферзь. Но запомнить не трудно: король уступает королеве клетку своего цвета. То есть белый ферзь в начале партии стоит на белой клетке (d1), а черный ферзь — на черной клетке (d8). А королям остаются поля е1 и е8.
Итак, все шахматные фигуры расставлены в нужном порядке на первой и восьмой горизонтали. А перед каждой фигурой в начале партии стоит маленький солдатик — пешка. У каждого игрока в начале партии есть целых восемь пешек, но каждая из них, если дойдет до конца доски, сможет превратиться в любую фигуру. Конечно, обычно пешку превращают в самую сильную фигуру.
Сила и ценность шахматных фигур
Единицей шахматной силы считается пешка.
За пешкой следуют конь и слон — их сила оценивается в три пешки. Между собой конь и слон считаются примерно равноценными: у них очень разный ход, но каждый имеет свои преимущества. Слон сильнее в открытых позициях, так как может контролировать сразу все клетки на диагонали. Слон умеет ставить такие приемы, как связка, вскрытый шах, рентген, а также часто помогает ферзю в матовой атаке. Конь же очень полезен в закрытых позициях, отлично маневрирует и перепрыгивает через препятствия, умеет ставить вилку и спертый мат.
Следующая по силе фигура — ладья. Ладья стоит пять пешек. Это значит, что ладья сильнее коня и слона, но конь и слон вместе будут стоить немного дороже, чем одна ладья. Ладья, как и слон, — дальнобойная фигура, которая может контролировать все клетки на линии, но ее преимущество в том, что ладья может взять под контроль любую клетку пустой шахматной доски за один ход, а слон может нападать только на поля одного цвета. Ладья при помощи короля может заматовать одинокого короля соперника (а один конь или один слон не смогут). А две ладьи могут поставить мат вражескому королю даже без помощи своего короля (это называется линейный мат).
И, наконец, самая сильная шахматная фигура — ферзь. Сила ферзя — 9 пешек. Ферзь умеет ходить как слон и ладья сразу, умеет делать все тактические приемы (кроме вилки), контролирует за один ход максимальное число полей на доске и может нападать на много фигур сразу. Чаще всего именно ферзь ставит мат королю соперника. По ценности один ферзь немного сильнее ладьи и слона или коня, но чуть слабее двух ладей.
А как же король? Король — бесценный! Знать ценность фигур нужно для того, чтобы понимать, размены каких фигур будут выгодны (например, выгодно съесть у соперника ладью, потеряв взамен коня, потому что ладья на 2 пешки дороже коня). А короля съесть или разменять нельзя — королю можно только поставить мат. В начале и середине партии король не силен — другие фигуры его обороняют, а он обычно стоит в надежно укрепленном месте. А вот когда на доске остается мало фигур, король становится очень важным — помогает поставить мат или проводить свои пешки в ферзя. Тогда его сила может быть равна или даже выше силы коня или слона.
Повторим ценность фигур на примере таблички:
Итак, теперь мы знаем, как правильно расставлять фигуры, а также особенности и силу каждой фигуры. А набить руку в игре с тренером, запомнить правила расстановки и отточить тактические приемы помогут индивидуальные онлайн-занятия по шахматам в школе Skysmart. Дарим до 3 уроков при первой оплате!
Источник
∀ x, y, z
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Глава 9. Независимость н доминирование шахматных фигур / Математика на шахматной доске // Гик Е. Я. |
Глава 9. Независимость н доминирование шахматных фигур / Математика на шахматной доскеГик Е. Я.Глава 9. Независимость и доминирование шахматных фигурМножество очень интересных и красивых задач на шахматной доске возникает при решении двух следующих комбинаторных проблем. 1. Какое максимальное число одноименных фигур (ферзей, ладей, слонов, коней или королей) можно расставить на шахматной доске так, чтобы никакие две из них не угрожали друг другу? 2. Какое минимальное число одноименных фигур (ферзей, ладей, слонов, коней или королей) можно расставить на шахматной доске так, чтобы они держали под обстрелом все свободные поля доски? Первое из этих чисел мы будем называть числом независимости для соответствующих фигур, а второе — числом доминирования. Для единства терминологии фигуры, которые не угрожают друг другу, будем называть независимыми, а фигуры, обстреливающие все свободные поля доски (доминирующие на доске), — доминирующими. Здесь мы имеем явную аналогию с рядом важных задач из теории графов. Чтобы убедиться в этом, приведем следующие определения. Множество вершин графа называется независимым, если никакие две из них не соединены между собой ребром. Среди независимых множеств существует хотя бы одно «максимально независимое», содержащее максимальное число вершин. Это число называется числом независимости для данного графа (или числом его внешней устойчивости). Множество вершин графа называется доминирующим, если каждая вершина вне этого множества соединена ребром хотя бы с одной вершиной, принадлежащей ему. Среди доминирующих множеств существует хотя бы одно «минимально доминирующее», содержащее минимальное число вершин. Это число называется числом доминирования для данного графа (или числом его внутренней устойчивости)36. Каждой шахматной фигуре можно поставить в соответствие граф, вершины которого расположены на всех 64 полях доски, а ребра соответствуют ходам этой фигуры. Иначе говоря, если фигура в состоянии сделать ход между двумя данными полями, то расположенные в них вершины соединены ребром (аналогично был введен граф при рассмотрении задачи о коне Аттилы). Теперь легко убедиться в том, что наша первая проблема заключается в определении числа независимости для графа данной фигуры, а вторая проблема — в определении числа доминирования. Установленная связь между чисто математическими объектами — графами и задачами о шахматных фигурах, как мы видели, довольно естественна, чем и объясняется большая популярность шахматных терминов и задач в литературе по теории графов. Многие задачи о графах, весьма сложные в общем случае, удается решить для графов шахматных фигур. Именно так обстоит дело и с задачами о независимости и доминировании на шахматной доске. Ниже мы найдем числа независимости и доминирования для графов всех шахматных фигур и, следовательно, разрешим для них обе наши проблемы. Попутно нами будут рассмотрены вопросы о подсчете числа «оптимальных» расстановок фигур, а также разлтные обобщения для досок n×n. Для удобства через А будем обозначать число независимости, а через D — число доминирования, индекс у этих букв указывает размер доски; так, Dn (Л) — число доминирования для ладей на доске n×n. Результаты наших исследований мы будем заносить в табл. 2, знаки вопроса означают, что соответствующие числа неизвестны (по крайней мере, автору). После каждой строки с числами N и D в таблще идет строка с числом «оптимальных» расстановок на доске — т. е. расстановок, в которых участвуют, соответственно, N или D указанных фигур. Остановимся теперь на каждой из шахматных фигур в отдельности. 1. Ферзь. Число независимости для ферзей на любой доске n×n найдено в предыдущей главе, имеем N2(Ф) = 1, N3(Ф) = 2, Nn(Ф) = n (n ≠ 2, 3). Формула для числа соответствующих расстановок в общем случае не известна. На обычной доске, как мы знаем, кожно расставить восемь независимых ферзей (рис. 43), причем существуют 92 различные расстановки. Число доминирования для ферзей на обычной доске, как, впрочем, и на досках 9×9, 10×10 и 11×11 (рис. 35, 39), равно пяти. Существует 4860 способов для расстановки пяти «ферзей-часовых» на доске 8×8. Как уже говори л ось, в общем случае формулу для Dn (Ф) никому найти не удалось (тем более неизвестно и число решений). 2. Ладья. Для ладьи все результаты получены в главе 6. Как мы знаем, Nn (Л) = Dn(Л) = n, а число расстановок соответственно равно n! и 2n n — n! На обычной доске имеется 8! расстановок восьми независимых ладей и 2×8 8 — 8! расстановок восьми доминирующих ладей. Источник |
