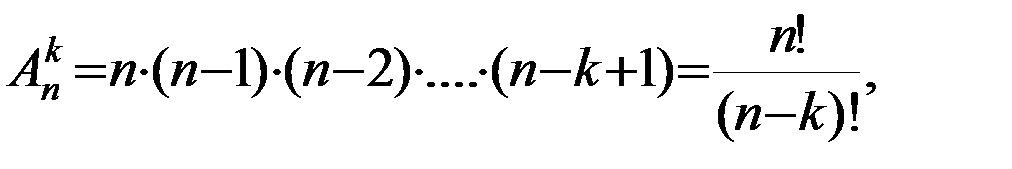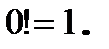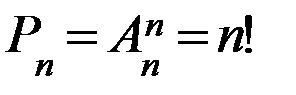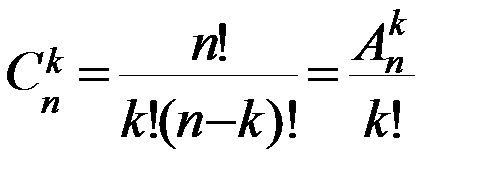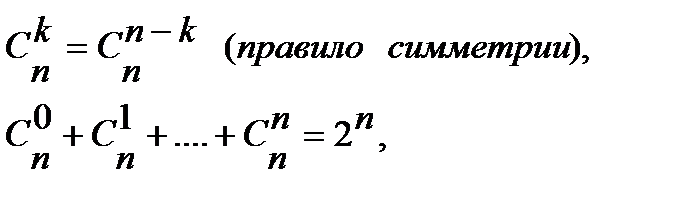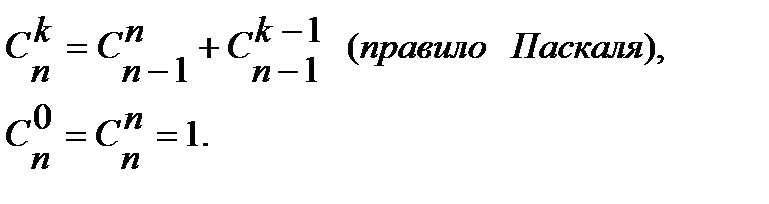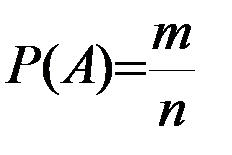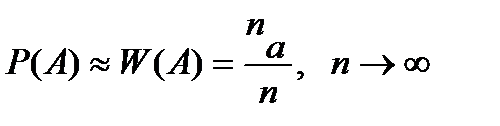Алгебраические действия над событиями.
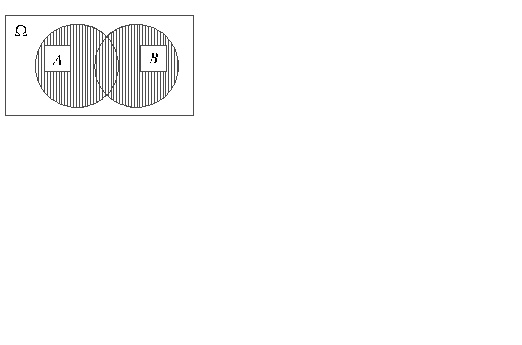
Суммой событий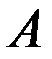 
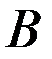
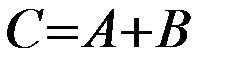
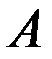
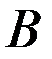
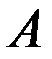
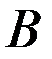
и 
называется событие 
, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий и (то есть или , или , или оба вместе, знак + читается или).
Приведем пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B — в том, что в мишень попадает 2-й. Событие С 
означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.
Аналогично суммой конечного числа событий А1, А2, . А k — называется событие А = А1 + А2 + . + А k, состоящее в наступлении хотя бы одного из событий А i (i = 1, 2, . k).
Из определения следует, что А + В = В + А.
Справедливо также и сочетательное свойство. Однако А+ А = А (но не 2А, как в алгебре).
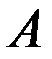
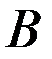
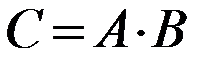
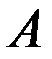
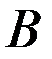
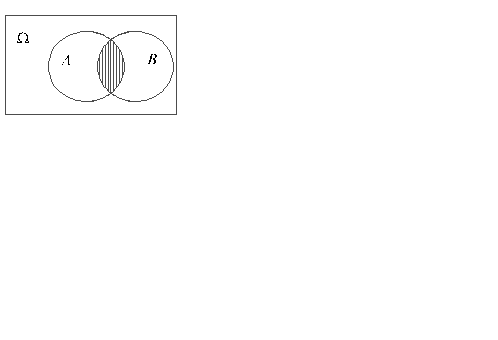
Произведением событий и называется событие 
, которое происходит тогда и только тогда, когда происходят оба события и (знак умножения читается как союз и).
На рисунке 3 пересечение событий А и Bизображено в виде заштрихованной области. В условиях приведенного выше примера событие A•B заключается в том, что в мишень попали оба стрелка.
Из определения следует, что АВ = ВА. Справедливы также сочетательный и дистрибутивный законы. Однако
Элементы комбинаторики.
Пусть дано множество, состоящее из n различных элементов.
Размещением из n элементов по k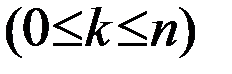 
называется любое упорядоченное подмножество данного множества, содержащее k элементов.
Два размещения различны, если они отличаются друг от друга либо составом элементов, либо порядком их расположения.
Число размещений из n элементов по k обозначают символом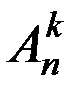 
и вычисляют по формуле:
где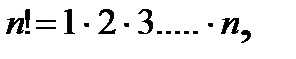 
причем 
Пример 1. Составить различные размещения по два элемента из элементов множества А= и подсчитать их число.
Решение. Из трех элементов можно образовать следующие размещения по два элемента: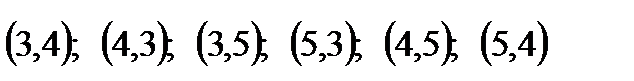 
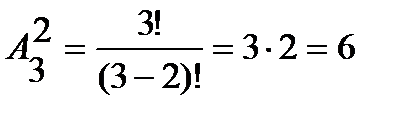
. Таким образом, всего их шесть. Однако число размещений можно посчитать и по формуле (1.1):
.
Пример 2. Сколькими способами 3 награды (за 1-е, 2-е и 3-е места) могут быть распределены между 10 участниками соревнований?
Решение. Будем считать, что каждый участник соревнований может получить не более одной награды. Выбрать 3-х участников из 10 можно следующим образом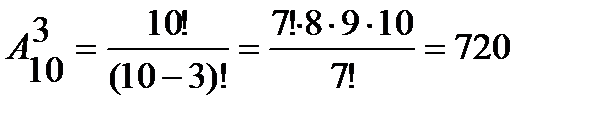 
, так как «призовые тройки» отличаются друг от друга либо составом участников, либо порядком их следования.
Перестановкой из n элементов называется размещение из n элементов по n элементов. Число перестановок обозначается символом Pn и вычисляется по формуле: 
Таким образом, указать ту или иную перестановку из n элементов значит выбрать определенный порядок этих элементов. Поэтому любые две перестановки отличаются друг от друга только порядком следования элементов.
Пример 3. Сколькими способами можно расставить на книжной полке десятитомник Д. Лондона, располагая их: 1) в произвольном порядке; 2) так, чтобы 1, 5 и 9 тома стояли рядом.
Решение. 1) Число способов расстановки 10 книг равно числу перестановок из 10 элементов, то есть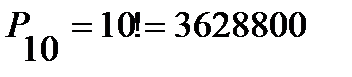 
;
2) Мысленно связав 1, 5 и 9 тома в одну связку, получим 8 «книг», то есть 7 книг и одну связку книг. Их можно расставить на полке 
. Каждому из этих способов расстановки соответствуют 
способов расстановки книг, находящихся в связке. Таким образом, число возможных расстановок 10 книг, чтобы три определенные книги стояли рядом (1, 5 и 9) равно: 
.
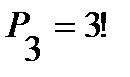
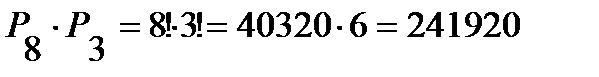
Сочетанием из n элементов по k 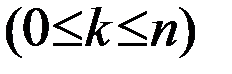называется любое подмножество данного множества, содержащее k элементов.
Любые два сочетания отличаются друг от друга хотя бы одним элементом (то есть отличаются только составом элементов). Число сочетаний из n элементов по k обозначается символом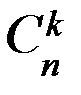 
и вычисляется по формуле: 
Для чисел 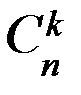справедливы следующие тождества:
Пример 4. В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее: 1) 3 гвоздики; 2) 6 гвоздик одного цвета; 3) 4 красных и 3 розовых гвоздики.
Решение. 1) Так как порядок выбора цветов не имеет значения, то выбрать 3 гвоздики из вазы, в которой стоят 16 гвоздик, можно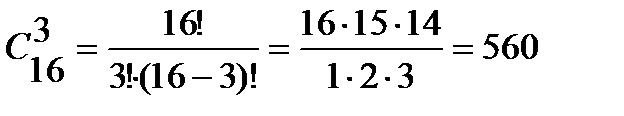 
способами;
2) Выбрать 6 гвоздик красного цвета можно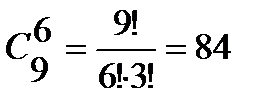 
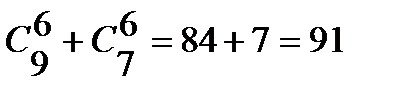
способами, а выбрать 6 гвоздик розового цвета можно 
способами. По правилу сложения выбрать 6 гвоздик одного цвета (красных или розовых) можно 
способом;
3) Выбрать 4 красных гвоздик из 9 имеющихся можно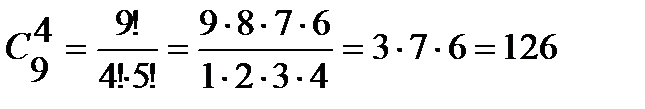 
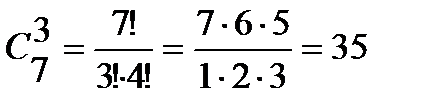
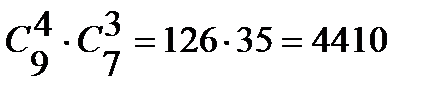
способами, а 3 розовых из имеющихся 7 можно 
способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения 
способами.
.4. Классическое и статистическое определение вероятности.
Пусть производится опыт с n равновозможными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными событиями. Случай, который приводит к наступлению события А, называется благоприятным этому событию.
Вероятностью события А называется отношение числа mисходов, благоприятствующих этому событию, к общему числу n исходов:
Из классического определения вероятности следуют следующие свойства:
1) вероятность достоверного события равна единице, то есть все исходы являются благоприятными (m = n):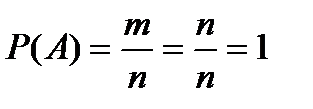 
;
2) вероятность невозможного события равна нулю (m =0):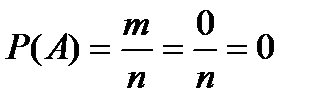 
;
3) вероятность случайного события есть положительное число, заключенное между нулем и единицей: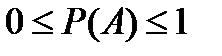 
.
Статистическое определение вероятности связывает понятие вероятности с эмпирическим (опытным) понятием относительной частоты случайного события W ( A ), которая находится по результатам серии опытов.
Относительной частотой случайного события А называется отношение числа опытов, в которых появилось данное событие na, к общему числу фактически произведенных опытов n: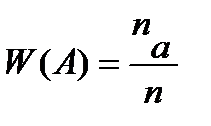 
.
Статистической вероятностью события А называется постоянное число, к которому приближаются значения частоты этого события по мере увеличения числа опытов: 
Пример 5.В городе имеется одиннадцать различных коммерческих банков. Господин «N» открыл по одному счету в пяти различных банках. Позднее четыре банка из одиннадцати изменили ставки процентов по вкладам. Найти вероятность того, что по двум вкладам господина ставки остались неизменными.
Решение. Господин выбирал банки случайным образом. Испытание – выбор пяти банков из имеющихся одиннадцати. A – событие, состоящее в том, что по двум вкладам господина, из имеющихся пяти, ставки остались неизменными, и, следовательно, по трем другим изменились.
, где 
— число всех исходов испытания (несовместимых, единственно возможных и равновозможных); 
— число исходов, связанных с наступлением события А ( 
— число вариантов выбора двух банков, из имеющихся семи, не изменивших ставки процентов, 
— число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов).
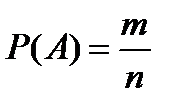
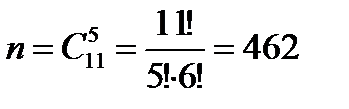
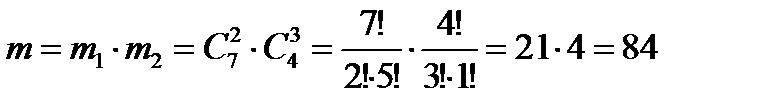
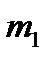
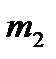
Таким образом,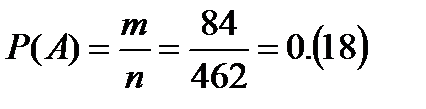 
.
Источник
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Комбинаторика – раздел математики, изучающий различные соединения (комбинации) элементов конечных множеств.
Пусть дано множество, состоящее из n элементов.
Размещениями из n элементов по k элементов ( 
) называется любое упорядоченное подмножество данного множества, содержащее k элементов.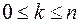
Два размещения различны, если они отличаются друг от друга либо составом элементов, либо порядком их следования.
Число размещений из n элементов по k элементов обозначается символом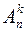 
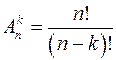
и вычисляется по формуле
.
Перестановкой из n элементов называется размещение из n элементов по n элементов. Любые перестановки отличаются друг от друга только порядком следования элементов.
Число перстановок из n элементов обозначается символом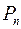 
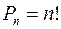
и вычисляется по формуле
.
Сочетанием из n элементов по k элементов ( ) называется любое подмножество данного множества, содержащее k элементов.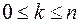
Любые два сочетания отличаются друг от друга только составом элементов.
Число сочетаний из n элементов по k элементов обозначается символом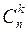 
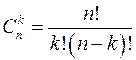
и вычисляется по формуле
.
Если при выборке k элементовиз n элементы возвращаются обратно, то полученные выборки представляют собой выборки с повторениями.
Число размещений из n элементов по k элементов с повторениями обозначается символом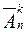 
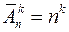
и вычисляется по формуле
.
Число сочетаний из n элементов по k элементов с повторениями обозначается символом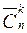 
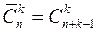
и вычисляется по формуле
.
Задачи
1.1.Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если:
а) цифры не повторяются; б) цифры могут повторяться; с) числа должны быть нечетными и цифры не повторяются.
Задачу решить двумя способами: используя формулы комбинаторики и используя основные правила комбинаторики.
1.2.На5 сотрудников выделено3 путевки.Сколькими способами их можно распределить, если: а) путевки различны; б) путевки одинаковы.
1.3.Сколько различных «слов» можно составить из всех букв слова ПРИЗМА? Сколько из них таких, в которых буквы Р и И стоят рядом? Сколько таких, в которых эти буквы не стоят рядом? (в комбинаторике под словами понимают любой набор букв, который не обязательно будет словом какого-нибудь языка).
1.4.Четыре студента сдают экзамен. Сколькими способами им могут быть выставлены положительные оценки?
1.5.Имеется 4 разных флага. На флагштоке поднимается сигнал, состоящий не менее чем из двух флагов. Сколько различных сигналов можно подать, если порядок флагов в сигнале учитывается?
1.6.В коробке 10 деталей, из них 7 стандартные. Сколькими способами можно взять из коробки 6 деталей таким образом, чтобы среди них было 4 стандартные детали?
1.7.В студенческой группе 12 девушек и 16 юношей. Сколькими способами можно выбрать двух студентов одного пола?
1.8.Из группы в 15 человек выбирают четырех участников эстафеты 800×400×200×100. Сколькими способами можно расставить спортсменов на этих этапах?
1.9.Сколькими способами можно расставить на книжной полке десятитомник произведений Д. Лондона, располагая их:
а) в произвольном порядке;
б) так, чтобы I, V и IX тома стояли рядом (в любом порядке);
в) так, чтобы I, II, IIIтома не стояли рядом (в любом порядке)?
1.10.Вкомнате имеется 7 стульев. Сколькими способами можно разместить на них 7 гостей? 3 гостя?
1.11.Студенты сдают 5 экзаменов, в том числе 2 экзамена по математике. Сколькими способами можно распределить экзамены, но так, чтобы экзамены по математике следовали один за другим? Не следовали один за другим?
1.12.Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькими способами он может выбрать приглашенных?
1.13.Имеется 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать: а) три любые гвоздики; б) шесть гвоздик одного цвета; с) четыре красных и три розовых гвоздики?
1.14.Группа туристов из 12 юношей и 7 девушек выбирает по жребию 5 человек для приготовления ужина. Сколько существует способов при которых в эту «пятерку» попадут: а) одни девушки; б) 3 юноши и 2 девушки; в) 1 юноша и 4 девушки; г) 5 юношей?
1.15.В магазине 7 видов тортов. Сколькими способами можно приобрести набор из трех тортов? А если имеется три вида тортов, а необходим набор из 7 тортов?
1.16.Пять человек вошли в лифт на первом этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
1.17.Найти число диагоналей выпуклого десятиугольника.
1.18.Собрание из 40 человек избирает председателя, секретаря и трех членов редакционной коллегии. Сколькими способами это можно сделать?
1.19.В купе железнодорожного вагона один напротив другого два дивана по четыре места. Из 8 пассажиров трое желают ехать по ходу движения поезда, двое – спиной. Сколькими способами можно разместить пассажиров с учетом их пожеланий?
1.20.В некотором государстве не было жителей с одинаковым набором зубов. Какова наибольшая численность этого государства?
1.21.В подъезде дома установлен замок с кодом. Дверь автоматически отпирается, если в определенной последовательности набрать четыре цифры из имеющихся 12. Некто, не зная кода, стал наудачу набирать различные комбинации из 4-х цифр. Какое наибольшее число попыток ему надо предпринять, чтобы дверь открылась?
1.22.12 человек прибыли в гостиницу, в которой есть один 4-местный, два 3-местных и один 2-местный номер. Сколькими способами их можно разместить в этих номерах?
Источник
