Сколькими способами можно расставить белые черные шашки

Учебные материалы для студентов

Методические указания, конспекты, лекции, контрольные, лабораторные работы, курсовые.

Дискретная математика

Задача 1. Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?

Решение:

Белые шашки можно расставить С 12 ₃₂ способами. После выбора 12 полей для белых шашек остается 32-12=20 полей для черных шашек, на которые их можно поставить С 12 ₂₀ способами. Всего по правилу произведения С 12 ₃₂С 12 ₂₀ способов.

Задача 2. В комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5 блюдец и 6 чайных ложек (все чашки, блюдца и ложки отличаются друг от друга). Сколькими способами они могут накрыть стол для чаепития (каждый получает одну чашку, одно блюдце и одну ложку)?

Решение:

Чтобы найти число способов, которыми могут быть расставлены чашки надо найти число размещений (без повторений) из 4 элементов по 3, блюдца — число размещений из 5 элементов по 3, ложки — число размещений из 6 элементов по 3. В решении используется формула размещений без повторений, так как здесь играет роль, какая из ложек (чашек, блюдец) будет выбрана, так как все чайные приборы отличаются друг от друга. Число способов, которыми могут быть выбраны 3 чашки, блюдца и ложки находится по правилу произведения: А 3 ₄*А 3 ₅*А 3 ₆=4*3*2*5*4*3*6*5*4=172800 способов.

Задача 3. Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд, так чтобы при этом два футболиста одной команды не стояли рядом?

Решение:

также в рубрике Контрольные, тесты:

Источник

Правила суммы и произведений

Комбинаторные задачи бывают самых разных видов, но большинство задач решается с помощью правила суммы и правила произведения .

Часто удается разбить все изучаемые комбинации на несколько классов, причем каждая комбинация входит в один и только один класс . Ясно, что в этом случае общее число комбинаций равно сумме чисел комбинаций во всех классах. Это утверждение и называется правилом суммы .

Правило суммы : если объект можно выбрать способами, а объект другими способами, то выбор «либо , либо » может быть осуществлен способами.

Второе правило — правило произведения . Часто при составлении комбинации из двух элементов известно, сколькими способами можно выбрать 1-й элемент, и сколькими способами второй, причем число способов выбора второго элемента не зависит от того, как именно выбран первый элемент.

Правило произведения : если объект выбран способами и после каждого из таких выборов, объект , в свою очередь может быть выбран способами, то выбор » и » в указанном порядке может быть осуществлен способами.

Задача 1 (о шашках)

Сколькими способами можно поставить на доску две шашки — белую и черную — так, чтобы белая шашка могла бить черную?

Правила игры в шашки известны.

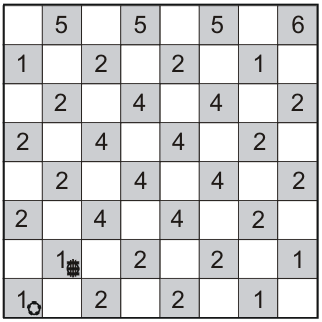
Сложность этой задачи состоит в том, что для разных положений белой шашки есть разное число положений черной шашки, при которых эту шашку можно бить ( рис. 7.1).

Если белая шашка стоит на поле , то существует лишь 1 положение, при котором она находится под боем. Если белая шашка стоит на поле , то число искомых положений черной шашки равно 4. Наконец, если белая шашка прошла в «дамки», на поле , то имеется 6 положений черной шашки, на которых ее можно бить белой шашкой.

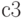
Складывая полученное число вариантов для каждой позиции, получим 87.

Ясно, что существует ровно столько же положений, при которых черная шашка может бить белую. А положений, при которых обе шашки могут бить друг друга, меньше ( рис. 7.2).

Например, если белая шашка стоит на краю доски, то ее нельзя бить, где бы ни стояла черная шашка. Поэтому всем полям на краю соответствуют нули. Точно так же находим числа, соответствующие другим полям. Складывая их, получаем, что искомая расстановка возможна 50 способами.

Найдем число положений, при котором ни одна из 2 шашек (черная или белая) не может бить другую. Эту задачу можно было бы решить так же, как и предыдущие, ставя белую шашку на каждое из черных полей и подсчитывая, сколькими способами можно поставить черную шашку так, чтобы ни одна из этих шашек не могла бить другую. Но, здесь проще свести задачу к уже решенной. Для этого сначала найдем общее число положений, которыми можно поставить на доску белую и черную шашки. Белую шашку можно поставить на любую из 32 клеток, следовательно, для черной останется 31 позиция. Отсюда вытекает, что расстановка возможна способами. Но из них 87 способов, при которых черная шашка бьет белую и 87 способов, при которых белая шашка бьет черную. Поэтому надо отбросить способа. Однако следует учесть, что при этом некоторые способы оказываются отброшенными дважды: из-за того, что черная шашка может бить белую шашку, и белая шашка может бить черную шашку. Таких положений 50. Поэтому число положений, в которых ни одна шашка не может бить другую, равно .

Источник

Информационный проект. Применение комбинаторики в играх (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

4. Число расстановок двух боевых ладей. Сколькими способами можно расставить на шахматной доске две атакующих (или защищающихся друг от друга) разноцветные ладьи?

Решение. По формуле находим, что N =2(n³ — n²). N =896.

5. Простая сила шахматных фигур. Абсолютную силу шахматной фигуры можно определить как число полей, которым она угрожает, или как вероятность дать этой фигурой простой шах королю на пустой доске.

Пусть ладья стоит на произвольной клетке. Тогда вражеский король может занимать любую из оставшихся 63 клеток. Ладья, независимо от места, которое она занимает, всегда угрожает 14 полям, и вероятность простого шаха, который может дать ладья королю, будет

Это и будет абсолютной силой ладьи.

Аналогично, но с учетом занимаемого места можно найти абсолютные силы коня, слона и ферзя и затем, соотнеся их между собой, определить относительные силы. Каковы относительные силы ладьи, коня, слона и ферзя?

Число полей, которым может угрожать конь, зависит от его положения на доске. Если он стоит в одном из четырех углов, то угрожает только двум полям. Рассмотрев все положения коня, находим абсолютную силу коня: fконь =(4×2 + 8×3 + 20×4 + 16×6 + 16×8 ); (64×64) =1/12.

Слон, стоящий на любой из 28 клеток четырех граничных горизонталей и вертикалей, угрожает 7 полям. Стоя на 20 полях следующей квадратной рамки, слон угрожает 9 полям т. д. Абсолютная сила слона равна: fслона = (28×2 + 20×9 + 12×11 + 4×13)/ (64×63) = 5/36.

Поскольку ферзь угрожает полям, как вместе взятые ладья и слон, то его абсолютная сила: fферзь =2/9 + 5/36 =13/36. Отнеся абсолютные силы фигур к общему знаменателю т36, находим относительные силы:

fконь = 3, fслон = 5, fладья = 8 b fферзь = 13.

С древних времен известно множество разновидностей шашечных игр. Известно, что в шашки (правда, отличающихся от наших) играли египетские фараоны. Затем игра проникла в Грецию и Древний Рим. Правила ее со временем изменялись. В гробнице египетского фараона Тутанхамона была найдена шашечная доска размером 3х10 клеток, отличающихся от принятых у нас. Однако с течением времени установились современные правила: шашки имеют два цвета, ходят они только вперед, взятие происходит перескакиванием через шашку соперника, на противоположном конце доски шашка превращается в дамку и т. д. Появление шашек на Руси связывают с именем киевского князя Владимира Мономаха.

Решим следующую задачу о шашках.

Сколькими способами можно поставить на доску две шашки – белую и черную так, чтобы белая шашка могла бить черную?

Сложность этой задачи состоит в том, что для разных положений черной шашки есть разное положение шашки, при которых эту шашку можно бить.

Поэтому здесь проще указать для каждого положения белой шашки число возможных положений черной шашки и сложить полученные результаты.

А положений, при которых обе шашки могут бить друг друга меньше. Например, если белая шашка стоит на краю доски, то ее нельзя бить, если бы ни стояла черная шашка. Поэтому всем полям на краю доски соответствует число 0. Точно также находим числа, соответствующие другим черным

полям. Они изображены на рисунке.

Наконец, найдем число положений белой и черной шашек, при котором ни одна из них не может бить друг друга.

Эту задачу можно было бы решить так же, как и предыдущие, ставя белую шашку на каждое из черных полей и подсчитывая, сколькими способами можно поставит черную шашку так, чтобы ни одна из этих шашек не могла бить другую. Сначала найдем общее число расположений на доске одной белой и одной черной шашки. Белую шашку можно поставить на любое из 32 черных полей. После этого для черной шашки останется 31 поле. Поэтому в силу правила произведения расстановка возможна 32х31=992 способами. Но среди этих способов есть 87, при котором черная шашка может бить белую. Поэтому надо отбросить 2х87=174 способа. Однако следует учесть, что при этом некоторые способы оказываются отброшенными дважды – из-за того, что в них и белая шашка может бить черную, и черная может бить белую. Мы видели, что существует 50 положений, в которых обе шашки могут бить друг друга. Поэтому число положений, в которых ни одна шашка не может бить другую, равно

В 1879 году американский составитель шахматных задач и этюдов, головоломок и различных игр Сэмюэль Лойд свел с ума Европу и Америку квадратной коробочкой с 15 шашками. Коробочка имела 16 полей, а на шашках были нанесены числа от 1 до 15. Одно поле коробочки было свободное. Требовалось, передвигая каждым ходом одну шашку на свободное поле перевести в стандартное положение, изображенное на рисунке, из положения, изображенного на рисунке

За решение задачи была предложена крупная сумма денег. Фабрикант, выпускавший игру, быстро разбогател – рассказывали, что священники не выпускали из рук коробочки с шашечками во время богослужения, машинисты решали задачу, ведя поезда, торговцы забывали открывать свои магазины. Но никому не удавалось найти решение проблемы.

Горячка прошла лишь после того, как в 1880 году была доказана неразрешимость задачи Лойда. Чтобы изложить это доказательство, надо знать, что такое беспорядок (или инверсия) в перестановке чисел.

Возьмем перестановку числа 3142. В ней 3 стоит перед 1 и 2., хотя и больше них. Это создает 2 беспорядка. Еще один беспорядок возникает из-за того, что число 4 стоит перед числом 2. Всего в этой перестановке 3 беспорядка.

Если переставить два рядом стоящих числа, то количество беспорядков изменится на 1: или увеличится на 1, или уменьшится на 1.. Поэтому если число беспорядков было четным (нечетным), то оно станет нечетным (четным). Четность числа беспорядков называют четностью перестановки.

Выясним, что произойдет с четностью перестановки, если переставить два далеких друг от друга числа a и b в перестановке …a … b… . Пусть между ними стоит r других чисел. Тогда перемещение можно выполнить в три этапа – сначала r перестановками соседних чисел поставить число а рядом с числом b, затем поменять местами а и b и, наконец, еще r перестановками соседних чисел отправить b на то место, где раньше стояло а. Всего сделаем 2r + 1 перестановку соседних чисел, т. е. обязательно нечетное число, а так как при каждой такой перестановке четность числа беспорядков меняется, то в конце всей

Теперь мы можем закончить анализ игры в15. Каждое расположение шашек в этой игре можно задать с помощью некоторой перестановки 16 чисел. Каждое перемещение шашки на свободное место означает перестановку ее номера с числом 16 – номера пустого места, поэтому каждое такое перемещение меняет четность перестановки. Тогда две перестановки чисел 1,2,…, 16, получаемые друг из друга четным числом таких попарных обменов местами, должны иметь одинаковую четность. Но в каждой перестановке участвует пустая клетка. А чтобы она под конец вернулась на прежнее место, она должна сделать столько же ходов влево, сколько и вправо, столько же ходов вверх, сколько и вниз. Значит, она должна сделать четное число ходов. Поэтому, все перестановки, получаемые из стандартной перестановки перемещениями шашек в коробке и имеющие пустую клетку в правом нижнем углу, должны иметь ту же четность, что и стандартная перестановка, т. е. быть четными. А позиции на рисунке соответствует нечетная перестановка, имеющая 1 беспорядок. Значит, перевести ее в стандартную невозможно.

Такие доказательства невозможности играют большую роль в комбинаторике.

Источник