Перестановки

Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.

Рассмотрим пример. Пусть имеются три книги. Обозначим их буквами а, b и с. Эти книги можно расставить на полке по-разному.

Если первой поставить книгу а, то возможны такие расположения книг:

Если первой поставить книгу b, то возможными являются такие расположения:

И наконец, если первой поставить книгу с, то можно получить такие расположения:

Каждое из этих расположений называют перестановкой из трех элементов.

Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке.

Число перестановок из п элементов обозначают символом Рп (читается «Р из n»).

В рассмотренном примере мы установили, что Р₃ = 6. Для того чтобы найти число перестановок из трех элементов, можно не выписывать эти перестановки, а воспользоваться комбинаторным правилом умножения. Будем рассуждать так. На первое место можно поставить любой из трех элементов. Для каждого выбора первого элемента есть две возможности выбора второго из оставшихся двух элементов. Наконец, для каждого выбора первых двух элементов остается единственная возможность выбора третьего элемента. Значит, число перестановок из трех элементов равно 3 • 2 • 1, т. е. 6.

Выведем теперь формулу числа перестановок из n элементов. Воспользуемся тем же способом рассуждений, который был использован для нахождения Р₃.

Пусть мы имеем л элементов. На первое место можно поставить любой из них. Для каждого выбора первого элемента на второе место можно поставить один из оставшихся n — 1 элементов. Для каждого выбора первых двух элементов на третье место можно поставить один из оставшихся n — 2 элементов и т. д. В результате получим, что

Р_n = n (n — 1) (n — 2) • . • 3 • 2 • 1.

Расположив множители в порядке возрастания, получим

Р_n = 1 • 2 • 3 • . • (n — 2)(n — 1)n.

Для произведения первых n натуральных чисел используют специальное обозначение: n! (читается «n факториал»).

Например, 2! = 1 • 2 = 2; 5!=1 • 2 • 3 • 4 • 5 = 120.

По определению считают, что 1! = 1.

Таким образом, число всевозможных перестановок из n элементов вычисляется по формуле

Пример 1. Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках?

Число способов равно числу перестановок из 8 элементов. По формуле числа перестановок находим, что

Р₈ = 8! = 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 = 40 320.

Значит, существует 40 320 способов расстановки участниц забега на восьми беговых дорожках.

Пример 2. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, б?

Из цифр 0, 2, 4, 6 можно получить Р₄ перестановок. Из них надо исключить те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с цифры 0. Число таких перестановок равно Р₃. Значит, искомое число четырехзначных чисел равно Р₄ — Р₃.

Р₄ — Р₃ = 4! — 3! = 24 — 6 = 18.

Пример 3. Имеется девять различных книг, четыре из которых — учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?

Сначала будем рассматривать учебники как одну книгу. Тогда на полке надо расставить не девять, а шесть книг. Это можно сделать Р₆ способами. В каждой из полученных комбинаций можно выполнить Р₄ перестановок учебников. Значит, искомое число способов расположения книг на полке равно произведению Р₆ • Р₄.

Источник

Типичная смысловая нагрузка: «Сколькими способами можно переставить n объектов?»

Пример 1.Сколькими способами можно расставить 8 участников финального забега на восьми беговых дорожках?

Решение:P₈= 8!=1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40320.

Пример 2.Сколькими способами можно составить расписание на один день, если в этот день предусмотрено 6 уроков по 6 разным предметам?

Решение:P₆= 6!=1 ∙2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720.

Пример 3.Сколькими различными способами можно разместить на скамейке 10 человек?

Решение:P₈= 8!=1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 ∙ 10 = 3628800.

Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их.

Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их.

Пример. В группе ТОП – 19 1/9 обучается 24 студентов. Сколькими способами можно составить график дежурства по колледжу, если группа дежурных состоит из трех студентов?

Решение:число способов равно числу размещений из 24 элементов по 3, т.е. равно А₂₄ 3 . По формуле находим

Сочетания-соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом; число их .

Таким образом, количество вариантов при сочетании будет меньше количества размещений.

Пример.Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?

Решение: Так как кнопки нажимаются одновременно, то выбор этих кнопок – сочетание. Отсюда возможно

Решение задач на вычисление вероятности с использованием элементов комбинаторики

В урне находится 10 шаров, из них 6 белых и 4 черных шара. Вынули из урны 2 шара. Какова вероятность того, что оба шара — белые?

Решение: Рассмотрим событие А – оба вынутых шара белого цвета.

Число всевозможных исходов равно количеству выборок 2 шаров из 10. Выборка без возвращения и без повторения, поэтому . Число исходов, благоприятствующих наступлению события А равно числу вариантов извлечения 2 белых шаров из 6, поэтому . Тогда .

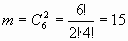
Ответ: .

Задача №2.

В секретном замке на общей оси 4 диска, каждый из которых разделен на 5 секторов, на которых написаны различные цифры. Замок открывается, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.

Решение: Рассмотрим событие А – замок будет открыт. Это событие равносильно тому, что цифры на дисках составляют определенное число.

Так как варианты набора цифр на дисках образуют выборку с возвращением (цифры могут повторяться) упорядоченную (при смене порядка цифр получается другое число), Благоприятный исход у этого события только один, поэтому

m = 1. Тогда

Задача №3.

Набирая номер телефона, абонент забыл последние 3 цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Найти вероятность того, что набраны нужные цифры.

Решение: Пусть событие А – набран верный номер. Тогда число всевозможных исходов равно числу трехзначных чисел, составленных из различных цифр. Так как в этом случае мы имеем выборку без возвращения (цифры различны), но упорядоченную (меняя цифры местами, получаем новое число), то Исход, благоприятствующий наступлению события А только 1. Поэтому

Задача №4.

В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток все открытки различны?

Решение: Пусть событие А — все проданные открытки различны.

Тогда число всевозможных исходов равно числу вариантов выбора 4 открыток. Эта выборка с возвращением (выбранные открытки могут быть одинаковые), неупорядоченная (так как важен лишь состав выборки, а не то, в каком порядке отобраны открытки). Значит Число исходов, благоприятствующих наступлению события А, есть число способов, которыми можно выбрать 4 различные открытки из 6 видов. Так как открытки теперь различны, то эта неупорядоченная выборка без повторения, значит Тогда

Ответ:

Источник

Элементы комбинаторики: перестановки, сочетания и размещения.

Элементы комбинаторики: перестановки, сочетания и размещения.

Определение: Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов .

Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д.

Термин «комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем, — всемирно известным немецким учёным.

Комбинаторные задачи делятся на: задачи на перестановки , задачи на размещение, задачи на сочетание

Определение: Факториал – это произведение всех натуральных чисел от 1 до n.

Обозначение: n ! = 1 · 2 · 3 · . · n.Читается: «эн факториал».

Пример: 4! = 1 · 2 · 3 · 4 = 24.

Задачи на перестановки

Сколькими способами можно расставить 3 различные книги на книжной полке?

Это задача на перестановки.

Решение: Выбираем одну из 3-х книг и ставим на первое место. Это можно сделать 3-мя способами.

Вторую книгу мы можем выбрать из 2-х оставшихся двумя способами, получаем 3·2 способов.

Третью книгу мы можем выбрать 1 способом.

Получится 3·2·1=6 способов.

Определение: Перестановками из n элементов называются комбинации из n элементов, отличающиеся друг от друга только порядком расположения в них элементов.

Типичная смысловая нагрузка: «Сколькими способами можно переставить n объектов?»

Пример 1. Сколькими способами можно расставить 8 участников финального забега на восьми беговых дорожках?

Решение: P ₈ = 8!=1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40320.

Пример 2. Сколькими способами можно составить расписание на один день, если в этот день предусмотрено 6 уроков по 6 разным предметам?

Решение: P ₆ = 6!=1 ∙2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720.

Пример 3. Сколькими различными способами можно разместить на скамейке 10 человек?

Решение: P ₈ = 8!=1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 ∙ 10 = 3628800.

Пример 4. Сколько слов можно получить, переставляя буквы в слове Гора?

Решение: P ₄ = 4!=1 ∙2 ∙ 3 ∙ 4 = 24.

Пример 5. Сколько различных шестизначных чисел, кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что цифры в числе не повторяются?

Решение: Чтобы число было кратным 5, цифра 5 должна стоять на последнем месте. Остальные цифры могут стоять на оставшихся пяти местах в любом порядке. Следовательно, искомое количество шестизначных чисел, кратных 5, равно числу перестановок из 5 элементов, т.е.

P ₅ = 5!=1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120.

Задачи на размещения

Имеется 5 книг и одна полка, такая что на ней вмещается лишь 3 книги.

Сколькими способами можно расставить на полке 3 книги?

Это задача на размещение.

Решение: Выбираем одну из 5-ти книг и ставим на первое место на полке. Это можно сделать 5-ю способами.

Вторую книгу мы можем выбрать 4-мя способами и поставить рядом с одной из 5-ти возможных первых.

Таких пар может быть 5·4.

Третью книгу мы можем выбрать 3-мя способами.

Получится 5·4·3 разнообразных троек. Значит всего способов разместить 3 книги из 5-ти 5·4·3 = 60.

Определение: Размещением из n элементов по k ( k ≤ n ) называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.

Типичная смысловая нагрузка: «Сколькими способами можно выбрать k объектов и в каждой выборке переставить их местами?»

Пример 1. Учащиеся второго класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета?

Пример 2. Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 7, 9?

Пример 3. В соревнованиях высшей лиги по футболу участвуют 18 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали между командами?

Пример 4. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?

Пример 5. Боря, Дима и Володя сели играть в карты. Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт)

– способами можно раздать 3 карты игрокам.

Пример 6. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

– способами можно рассадить в поезде 4 человека.

Задачи на сочетания

Сколькими способами можно расставить 3 тома на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 5 книг?

Это задача на сочетания.

Решение: Книги внешне неразличимы. Но они различаются, и существенно! Эти книги разные по содержанию. Возникает ситуация, когда важен состав элементов выборки, но несущественен порядок их расположения.

123 124 125 134 135 145

Определение: Сочетанием из n элементов по k ( k n ) называется любое множество, составленное из k элементов, выбранных из данных n элементов (не имеет значения, в каком порядке указаны элементы).

Типичная смысловая нагрузка: «Сколькими способами можно выбрать k объектов из n ?»

Пример 1. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

Пример 2. На тренировках занимаются 12 баскетболистов. Сколько может быть организовано тренером разных стартовых пятерок?

Пример 3. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Пример 4. Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

Пример 5. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?

Решение: Т.к. двое мальчиков войдут в команду, то остается отобрать 3 из 8. Для выборки важен только состав (по условию все члены команды не различаются по ролям).

Пример 6. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?

Решение: В одной игре участвуют 2 человека, следовательно, нужно вычислить, сколькими способами можно отобрать 2-х человек из 15, причем порядок в таких парах не важен.

Пример 7. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?

Решение: Различных дробей из 6 чисел: 3, 5, 7, 11, 13, 17 можно составить

штук ( способами выбираем два числа из 6, и двумя способами составляем из них дробь, сначала одно число – числитель, другое – знаменатель и наоборот).

Из этих 30 дробей 15 будут правильные.

Пример 8. Боря, Дима и Володя сели играть в карты. Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт)

– способами можно извлечь 3 карты из колоды. Теперь рассмотрим, какую-нибудь одну из семи тысяч ста сорока комбинаций, например: король пик, 9 червей , 7 червей. Эти 3 карты можно «переставить» между Борей, Димой и Володей P ₃ =3!=6способами. Тогда способами можно сдать по одной карте 3-м игрокам.

Правило сложения комбинаций

Знак «плюс» следует понимать и читать как союз ИЛИ.

Задача. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать 2-х человек одного пола?

Решение: Условие «выбрать 2-х человек одного пола» подразумевает, что необходимо выбрать двух юношей или двух девушек:

– способами можно выбрать 2-х юношей;

– способами можно выбрать 2-х девушек;

Таким образом, двух человек одного пола (без разницы – юношей или девушек) можно выбрать: способами.

Пример 1. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

Решение: Не менее 2-х человек, т.е. 2+7 или 3+6 или 4+5 человек (5+4, 6+3, 7+2 – те же самые комбинации).

В каждой выборке важен только состав, т.е. члены подгруппы не различаются по ролям, т.е. выборки – сочетания из n различных элементов по m элементов.

Число выборов из 2-х человек:

Число выборов из 3-х человек:

Число выборов из 4-х человек:

Применяем правило сложения: способов.

Правило умножения комбинаций

Знак «умножить» следует понимать и читать как союз И.

Задача. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно составить пару из юноши и девушки?

– способами можно выбрать 1 юношу;

– способами можно выбрать 1 девушку.

Таким образом, 1-го юношу и 1 девушку можно выбрать: способами.

Пример 1. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой – 6 мужчинам, по третьей – 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?

Решение: Имеем 14 претендентов и 13 рабочих мест. Сначала выберем работников на первую специальность, то есть 4 женщин из 6:

Далее выберем мужчин на вторую специальность:

Осталось 2 женщины, 2 мужчин и 3 вакантных места, которые, по условию, могут занять любые из четырех оставшихся человек.

Это может быть сделано 2 вариантами:

1 женщина и 2 мужчин (выбираем женщину способами)

1 мужчина и 2 женщины (выбираем мужчину способами).

В итоге получаем 15 · 28 · (2+2)=1680.

Пример 2. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую – 5 и в третью – 12. Сколькими способами это можно сделать.

Решение: Создавая первую бригаду, отбирают 3 человека из 20, создавая вторую – 5 из оставшихся 17, создавая третью – 12 из оставшихся 12. Для выборок важен только состав (роли членов бригады не различаются).

Создавая сложную выборку (из 3-х бригад), воспользуемся правилом умножения:

Пример 3. Сколькими способами может быть сдана выигрышная комбинация из 2-х карт при игре в «очко»?

Для тех, кто не знает: выигрывает комбинация 10 + ТУЗ (11 очков) = 21 очко и будем считать выигрышной комбинацию из 2-х тузов.

способами может быть сдана десятка и туз («каждая десятка с каждым тузом»);

способами может быть сдана пара тузов.

Итого: выигрышные комбинации.

Пример 4. Сколько существует трёхзначных чисел, которые делятся на 5?

В разряде сотен можно записать любую из цифр.

В разряде десятков можно выбрать любую из 10 цифр:

По условию, число должно делиться на 5. Число делится на 5, если оно заканчивается на 5 либо на 0. Таким образом, в младшем разряде нас устраивают 2 цифры.

Итого, существует: трёхзначных чисел, которые делятся на 5.

Перестановки с повторениями

У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?

Решение:Имеем набор <я, я, г, г, г>. Всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняются местами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2! · 3!.

В итоге получаем

Пример 1: Сколько различных буквосочетаний можно получить перестанов-кой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?

Решение: Всего: 11 карточек, среди которых буква:

К – повторяется 3 раза;

О – повторяется 3 раза;

Л – повторяется 2 раза;

Ь – повторяется 1 раз;

Ч – повторяется 1 раз;

И – повторяется 1 раз.

По формуле количества перестановок с повторениями:

Пример 2: Сколько слов можно получить, переставляя буквы в слове Институт?

Решение: В слове «институт» 8 букв, из них две буквы «и», три буквы «т» и по одной букве «н», «с» и «у». Поэтому всего можно получить перестановками букв различных слов.

Пример 3: Алексей занимается спортом, причём 4 дня в неделю – лёгкой атлетикой, 2 дня – силовыми упражнениями и 1 день отдыхает. Сколькими способами он может составить себе расписание занятий на неделю?

Решение: По формуле количества перестановок с повторениями:

способами можно составить расписание занятий на неделю.

Пример 4: Сколько чисел, больших 3000000, можно составить из цифр 3, 2, 2, 1, 1, 1, 0.

Решение: На первом месте обязательно должна стоять тройка. Оставшиеся 6 цифр образуют перестановку с повторениями:.

Сочетания с повторениями

В студенческой столовой продают сосиски в тесте, ватрушки и пончики. Сколькими способами можно приобрести пять пирожков?

Решение ( I способ.) :Обратите внимание на критерий сочетаний с повторениями – по условию на выбор предложено не множество объектов как таковое, а различные виды объектов; при этом предполагается, что в продаже есть не менее пяти хот-догов, 5 ватрушек и 5 пончиков.

Что может быть в выборке?

Варианты: 5 хот-догов, 5 ватрушек, 5 пончиков, 3 хот-дога + 2 ватрушки, 1 хот-дог + 2 ватрушки + 2 пончика и т.д. Всего 21 способ.

Ответ: 21 способ.

Типичная смысловая нагрузка: «Для выбора предложено n множеств, каждое из которых состоит из одинаковых объектов. Сколькими способами можно выбрать m объектов?»

Используя формулу количества сочетаний с повторениями, получаем

способом можно приобрести 5 пирожков.

Пример 1: В кошельке находится достаточно большое количество рублей, 2-х, 5-ти и десятирублёвых монет. Сколькими способами можно извлечь три монеты из кошелька?

Решение: Используя формулу количества сочетаний с повторениями, получаем

способами можно выбрать 3 монеты из кошелька.

Пример 2: В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений?

Размещения с повторениями

Сколько существует четырёхзначных пин-кодов?

Решение:Для решения задачи достаточно знаний правил комбинаторики:

способами можно выбрать первую цифру пин-кода и способами – вторую цифру пин кода и столькими же способами – третью и столькими же – четвёртую. Таким образом, по правилу умножения комбинаций, четырёхзначный пин-код можно составить: способами.

Типичная смысловая нагрузка: «Дано множество, состоящее из n объектов, при этом любой объект можно выбирать неоднократно. Сколькими способами можно выбрать m объектов, если важен порядок их расположения в выборке?

В частности, возможен случай, когда из n имеющихся объектов m раз будет выбран какой-то один объект».

Пример 1: Согласно государственному стандарту, автомобильный номерной знак состоит из 3 цифр и 3 букв. При этом недопустим номер с тремя нулями, а буквы выбираются из набора А, В, Е, К, М, Н, О, Р, С, Т, У, Х (используются только те буквы кириллицы, написание которых совпадает с латинскими буквами).

Сколько различных номерных знаков можно составить для региона?

– способами можно составить цифровую комбинацию автомобильного номера, при этом одну из них (000) следует исключить

– способами можно составить буквенную комбинацию автомобильного номера.

По правилу умножения комбинаций, всего можно составить

Пример 2: Человек, пришедший в гости, забыл код, открывающий дверь подъезда, но помнил, что он составлен из нулей и единиц и всего имеет четыре цифры. Сколько вариантов кода в худшем случае ему придётся перебрать, чтобы открыть дверь?

Пример 3: Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается?

Решение: Подсчитаем количество чисел от 1 до 999999 в записи которых нет единиц. Каждую цифру можно выбрать 9 способами (любая цифра кроме 1), поэтому все 6 цифр можно выбрать 9 6 способами. При этом один вариант (000000) нужно убрать, так как число 0 не рассматривается. Получаем всего 9 6 −1=531440 чисел. Так как всего чисел 1 000 000, то видно, что чисел без единицы среди чисел от 1 до 1 000 000 больше, чем тех, в записи которых единица есть.

Ответ: чисел без единицы больше.

(разработка + презентация) на тему «Комбинаторика для школьников любого возраста»

5. http :// infourok . ru / material . html ? mid =4205 – Урок математики в 7 классе на тему «Комбинаторика»

6. http :// festival .1 september . ru / articles /603009 / – «Комбинаторика – это . » (урок конструирования комбинаторных задач)

8. Математика. 6 класс: Учеб. для общеобразоват. учеб. заведений/Г.В. Дорофеев, С.Б.Суворова, И.Ф.Шарыгин и др.; Под ред. Г.В.Дорофеева, И.Ф.Шарыгина. – 7-е изд., стереотип. – М.: Дрофа, 2010. -416 с.: ил.

Источник