Сколькими способами можно расселить 8 студентов по 3 комнатам одноместную трехместную четырехместную

дискретная-математика — Сколькими способами можно поселить 7 студентов в три комнаты

Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?

задан 7 Ноя ’19 19:10

@man123, по-моему, 105 способов. Есть 7 способов поселить одного из студентов в одноместную. Затем в двуместную селим 2 из 6 оставшихся, это 15 способов, а остальных четырёх ровно одним способом в 4-местную, и того $%7\cdot 15\cdot 1=105$%.

@man123, 2) для проверки можно в обратную сторону прокрутить. Селим 4 из 7 в 4-местную, это 35 способов, затем 2 из оставшихся трёх селим в двуместную, это ещё 3 способа, и остался один студент, его поселим в 1-местную, итого $%35\cdot 3\cdot 1=105$%, всё сошлось.

@man123, 3) можно сделать задачу интереснее, если ввести дополнительные ограничения. Например, пусть среди студентов будут как парни, так и девушки, и пусть будет запрещено селить девушек и парней в одной комнате.

А теперь вопрос авторам задачи. Вы где видели одноместные комнаты в студенческих общагах? Такого люксуса даже в Гарварде нет!

@Казвертеночка, Вы где видели одноместные комнаты в студенческих общагах? Такого люксуса даже в Гарварде нет! — фи, Гарвард отстой. у нас в универе в общагах были блоки из двух комнат — трёхместной и одноместной.

@Казвертеночка: в Главном Здании МГУ я жил и в одноместных, и в двуместных, а большие комнаты могли быть и на 4 места. Так что всё правдоподобно.

@all_exist, @falcao, спасибо, теперь буду знать. Тем не менее, моё личное мнение таково, что селить студента одного в комнате не совсем полезно, как для самого студента, так и для общества. Студент замкнётся в себе и утратит социальные навыки, станет нелюдимым, одичает. Или даже, упаси Господь, руки на себя наложит. И потом, есть люди, которые панически боятся спать одни.

@Казвертеночка: мы, будучи аспирантами, жили вдвоём в блоке, но у каждого была своя комната. А общение при этом было очень «интенсивным», то есть мы друг у друга постоянно собирались в компании. А если бы жили с соседями, то это было бы трудно, так как шумное общество кому-то может мешать. А сама традиция вполне «каноническая» — Царскосельский Лицей, «кельи», и так далее.

Источник

Сочетания с повторениям

Ответ: 2520 перестановок.

Пример 2.4: Сколькими способами можно расселить 8 студентов по 3 комнатам: одноместной, трехместной и четырехместной?

.

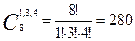
Ответ: 280 способов.

§3. Размещения

Рассмотрим теперь такие перестановки из n различных элементов, в которых участвуют не все, а только определенное количество элементов.

Определение 3.1:Размещенияминазывают комбинации, составленные из n различных элементов по k элементам, которые различаются либо составом элементов, либо их порядком.

Число всех возможных размещений определяют по формуле:

.

Пример 3.1: Сколькими способами из 7 книг можно отобрать 3 и расставить их на 3 места на книжной полке?

1 способ. n = 7, k =3.

.

2 способ. Эту задачу можно также решить по принципу произведения.

Книги должны занять 3 места. На 1 место можно поставить любую из 7 книг, на 2 место – любую из оставшихся 6, а 3 место может заполнить любая из оставшихся 5 книг. Таким образом, общее количество способов равно 7*6*5=210.

Ответ: 210 способов.

Пример 3.2: Определить количество телефонных номеров, состоящих из 5 различных цифр.

.

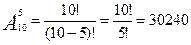
Ответ: 30240 телефонных номеров.

Размещения с повторениями.

Если каждый из k элементов упорядоченного множества может быть выбран n способами, независимо от других, то число способов выбора всех k элементов вычисляется по формуле:

Пример 3.3: В НИИ работает 4 курьера А, В, С, D. Сколько существует способов рассылки 7 писем в 7 различных организаций, если доставка писем осуществляется только курьерами, работающими в НИИ?

.

Ответ: 16384 способа.

Пример 3.4: В кабину лифта 9-этажного здания вошло 3 пассажира A, B, C, каждый из которых может выйти на любом из 8 этажей. Сколькими способами может осуществиться разгрузка лифта?

.

Ответ: 512 способов.

§4. Сочетания

Определение 4.1.:Сочетанияминазываюткомбинации, составленные из n различных элементов по k элементам, которые отличаются хотя бы одним элементом.

Число сочетаний определяется по формуле:

.

Замечание 4.1. Разница между размещениями и сочетаниями состоит в том, что в размещениях порядок элементов учитывается, а в сочетаниях – нет.

Пример 4.1.: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

.

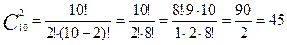
Ответ: 45 способов.

Пример 4.2.: Сколькими способами можно составить комиссию из 3 х человек, выбирая их из 4 х супружеских пар, если:

а) в комиссию могут входить любые трое из данных 8 человек;

б) комиссия должна состоять из двух женщин и одного мужчины?

а) В комиссии не играет роли порядок членов, поэтому

.

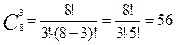
б) двух женщин можно отобрать способами. Затем одного мужчину можно отобрать способами. Всю комиссию можно составить

.

Ответ: 24 способами.

Сочетаниями из n элементов по k элементов с повторениями называются группы, содержащие k элементов, причём каждый элемент принадлежит одному из n типов. Число различных сочетаний из n элементов по k элементам с повторениями вычисляется по формуле:

Пример 4.3.: В кондитерской продаются пирожные 5 видов: бисквитные, корзиночки, буше, эклеры, трубочки. Сколькими способами можно купить 12 пирожных?

.

Ответ: 4368 способов.

ГЛАВА 5. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ.

§1. Основные понятия

Определение 1.1.Граф G, по существу,есть набор из 2 х множеств любой природы – непустого множества вершин V и множества ребер E , причем каждому ребру соответствуют две концевые вершины, которые, вообще говоря, могут и совпадать.

Определение 1.2. Вершина,соединенная ровно с одним ребром,исамо это реброназываютсяконцевыми или висячими.

Определение 1.3.Различные ребра, соединяющие две вершины, называются кратнымиили параллельными.

Определение 1.4.Ребра с совпадающими концами называютсяпетлями.

Определение 1.5.Граф G, имеющий n вершин, часто называютn – графом;если, кроме того, G содержит m ребер, то G – (n,m) граф.

Определение 1.6. Если e = uv некоторое ребро данного графа, то вершины u, v называются смежными.

Определение 1.7. Ребро e и вершина v инцидентны, если v – концевая вершина для e.

Определение 1.8. Ребра e и f называются смежными, если они имеют общую концевую вершину.

Определение 1.9. Две вершины, инцидентные одному и тому же ребру, называются соседними или смежными.

Определение 1.10. Степенью вершины v называется число ребер, инцидентных этой вершине, причем любая вершина учитывается дважды. Обозначение: deg_Gv или deg v.

Определение 1.11. Граф H называют подграфом графа G, если VHÍVG и EHÍEG.

Определение 1.12. Если VH=VG, то подграф H называется остовным подграфом.

Определение 1.13.Ориентированным графом G или орграфом G называется тройка (V, E, j), где j:E®V 2 =V´V, ставящего в соответствие каждому элементу eÎE упорядоченную пару элементов v₁v₂ÎV, называемых концами ребра e.

Определение 1.14. Если j(e)=v₁v₂ – упорядоченная пара, т.е. v₁v₂¹v₂v₁, то ребро e называется ориентированной дугой, исходящей из вершины v₁ и входящей в вершину v₂; v₁называется началом дуги e, а v₂ – концом дуги. Если j(e)=v₁v₂— неупорядоченная пара, то ребро e называется неориентированным.

§2. Способы задания графов

1) Перечисление. Список ребер графа с указанием их концов и добавлением списка изолированных вершин.

2) Матрица соседства (смежности) вершин графа G.

Пусть G – любой n-граф. Упорядочим множество вершин графа VG=1, v_{2, ¼,} v_n>, т.е. занумеруем вершины графа числами от 1 до n.

Определим матрицу смежности B графа G. B – квадратная матрица размерности n, строки и столбцы которой соответствуют вершинам графа, причем неотрицательный элемент b_ij равен числу ребер, идущих из вершины v_i в вершину v_j ( вообще говоря, b_ij¹b_ji, однако для неориентированных графов матрица соседства симметричная). Для несмежных вершин соответствующий элемент матрицы равен 0. При i=j каждую петлю учитываем дважды.

Пример 2.1. Определить матрицу смежности вершин для графа G.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Сколькими способами можно расселить девять студентов в трёх комнатах?

Сколькими способами можно расселить 15 студентов?
сколькими способами можно расселить 15 студентов в 5 комнат по 3 человека?

Сколькими способами можно выбрать трёх кроликов различных цветов?
Здравствуйте! Не могу понять, как решить задачу: «Сколькими способами можно выбрать трёх кроликов.

Сколькими способами можно разделить изготовление одинаковых деталей на трёх станках
Доброго времени суток. Помогите решить задачу, пожалуйста. Сколькими способами можно разделить.

Сколькими способами можно отправить 15 студентов на практику?
Сколькими способами можно отправить 15 студентов на практику в 15 предприятий, если 3 предприятия.

Как будто не надо. Сочетания же.

Добавлено через 5 минут
Я имел в виду, что комнаты (ящики) различимы, пронумерованы., Что для комнат было бы естественно.
Если же они неразличимы, то есть нам важно, кто с кем оказался, не важно — где, тогда, похоже, вы правы.

Добавлено через 15 минут
Да, Комбинаторика — штука тонкая! В ней важна различимость объектов. Но приняты некоторые умолчания. Люди — различимы. Этажи в лифте — тоже (у них есть номера) Шары, если они не пронумерованы — нет.
Имхо, комнаты в общежитии умеют номера. Как по-вашему?

я ровно об этом! )) к сожалению, ОЧЕНЬ часто в подобных задачах не конкретизируется различимость объектов, по которым «раскладываются» другие объекты

ну, смотрите, Вы сами пишете — «Шары, если они не пронумерованы — нет»; «. ЕСЛИ они не пронумерованы». а если они не пронумерованы, разве мы не можем их пронумеровать? )) (зачем — другой вопрос, но можем же)
точно так же, если что-то пронумеровано, то должны ли мы априори различать эти объекты С ТОЧКИ ЗРЕНИЯ ПОСТАНОВКИ ЗАДАЧИ? по-моему, не факт, ведь, вообще говоря, мы всегда можем пронумеровать все, что угодно

и в этой задаче про комнаты, почему мы (Вы )) решили, что важно, какая тройка попадет именно в ту или иную комнату?
поэтому, отвечая на Ваш вопрос . «комнаты в общежитии имеют номера. Как по-вашему?» — по-моему — однозначного ответа нет, пока это явно не указано в условии ))

ну, кам-он, почему же они непременно с номерами? может, номера со всех дверей сбиты.. и да, Вы можете возразить, что, мол, не вопрос, давайте их сами как-то пронумеруем, но так тогда это ровно то, что я говорю, — мы всегда можем пронумеровать все, что угодно
т.е. мы можем нумеровать непронумерованное, равно как и игнорировать нумерацию у пронумерованного; выбор определяется только тем, как мы трактуем условие задачи (а они, задачи, как было отмечено выше, частенько допускают двоякую трактовку, к сожалению), и сия трактовка определяется исключительно тем, как решающий ее понимает

вот по этой конкретной задаче лично я НЕ считаю, что комнаты имеют номера, т.е. я понимаю задачу как сколькими способами мы можем разделить 9 человек на 3 группы по 3 в каждой, только и всего

это же классическая задача — то же самое, что есть 9 человек, нужно разделить их на 3 команды по 3; как Вы ее решите? будете делить на 3! или нет? а вот это зависит, правда? Вы можете ПРЕДПОЛОЖИТЬ, что команды имеют номера с 1го по 3ий (или любые другие, не важно), и тогда будете решать так, как решаете с комнатами; а я не буду этого предполагать и разделю на 3! )) кто будет прав? да оба! ))

Добавлено через 13 минут
. при этом, свое решение я буду считать «более логичным» ))
а вот если бы в задаче было ДОПОЛНИТЕЛЬНОЕ условие, типа, одна из команд будет играть в четвертьфинале, другая в полуфинале, а третья в финале, то тогда правильным будет «Ваше» решение

с моей точки зрения, в задаче от ТС нет никаких причин додумывать и считать, что комнаты пронумерованы (пусть и может казаться, что для всех комнат на свете «логично» быть пронумерованными )); смысл в том, что мое понимание условия задачи не зависит от пронумерованности или «непронумерованности» комнат — это вообще не имеет никакого значения

Источник