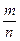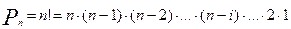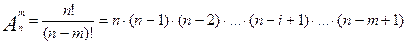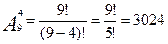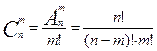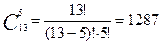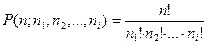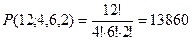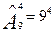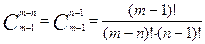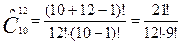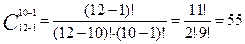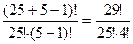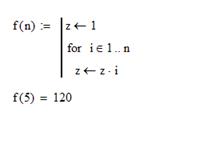Сколькими способами можно рассадить за круглым столом 6 человек если не существенно

Сколькими способами можно рассадить 6 человек за столом по кругу

Добрый день.
Есть задача: Сколькими способами можно рассадить 6 человек за столом: а) в ряд; б) по кругу; в) по кругу, при условии, что места не имеют номеров?

Под а) получаю 6!=720
Под б) 6!/6=120
А вот под в) не очень понимаю. Разве будет как то отличаться от случая под буквой б)? Помогите пожалуйста.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Сколькими способами можно рассадить в поезде 4 человек?
1. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человек при.

Сколькими способами можно разместить 8 человек за столом, у которого стоит 8 стульев?
Сколькома способами можно разместить 8 человек за столом, у которого стоит 8 стульев?

Сколькими способами 6 человек разместиться за столом, если имеет значение, на каком месте сидеть?
3. Решить задачу, используя а) правило произведения: б) формулы комбинаторики: Сколькими способами.

Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.

Сколькими способами 10 мальчиков и 10 девочек можно рассадить
Сколькими способами 10 мальчиков и 10 девочек можно рассадить за 10 парт при условии, что за одной.

Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.

Сколькими способами группу из 30 студентов можно рассадить по 36 стульям
Прошу проверить задание. Сколькими способами группу из 30 студентов можно рассадить по 36.

Сколькими способами можно рассадить этих людей, чтобы знакомые сидели рядом?
Помогите пожалуйста с задачами. Для закрытия всех долгов не хватает только этого 1. Среди 12.

Сколькими способами можно их рассадить за 10 партами, так чтобы за одной партой не сидели 2 девочки
В классе 12 мальчиков и 8 девочек. Сколькими способами можно их рассадить за 10 партами, так чтобы.

Источник

Сколькими способами можно рассадить 6 участников за круглым столом?

Математика | 10 — 11 классы

Сколькими способами можно рассадить 6 участников за круглым столом?

1) 6 * 5 * 4 * 3 * 2 * 1 = 720 вариантов ))))))))))))))))))))))))))).

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватить месть?

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватить месть.

А если этих же участников рассадить по 9 человек за каждый стол, то два стола останутся не занятыми.

Сколько человек участвовало на собрании?

У круглого стола поставили 4 стула?

У круглого стола поставили 4 стула.

Сколькими способами можно рассадить на эти стулья : а) 4 — х детей ; б) 3 — х детей ; в) 2 — х детей.

Если участников собрания рассадить по шесть человек на каждый стол, то троим не хватит месть?

Если участников собрания рассадить по шесть человек на каждый стол, то троим не хватит месть.

А если этих же участников рассадить по девять человек за каждый стол, то два стола останутся не занятыми.

Сколько человек участвовала на собрании?

Сколькими способами могут разместиться 5 человек вокруг круглого стола?

Сколькими способами могут разместиться 5 человек вокруг круглого стола.

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватит мест?

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватит мест.

А если этих же участников рассадить по 9 человек за каждый стол, то два стола останутся не занятыми.

Сколько человек участвовало на собрании?

За круглым столом расположились 30 взрослых участников дискуссии так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина?

За круглым столом расположились 30 взрослых участников дискуссии так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина.

Сколько женщин сидело за круглым столом?

За круглым столом 30 участников дискуссии сели так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина?

За круглым столом 30 участников дискуссии сели так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина.

Сколько женщин сидело за круглым столом?

Сколькими способами можно рассадить семь человек за круглый стол?

Сколькими способами можно рассадить семь человек за круглый стол.

Сколькими способами можно рассадить 7 лиц за столом, где поставлено 7 приборов?

Сколькими способами можно рассадить 7 лиц за столом, где поставлено 7 приборов.

У круглого стола поставили 4 стула?

У круглого стола поставили 4 стула.

Сколькими способами можно рассадить на эти стулья А) 4 ребёнка Б)3 ребёнка В)2 ребёнка.

На странице вопроса Сколькими способами можно рассадить 6 участников за круглым столом? из категории Математика вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

√2 — 2. Там есть линия.

(х — 1)(3х + 2) х — 1 = — — — — — — — — — — — — — — — — — = — — — — — — — — — — — — (3х — 2)(3х + 2) 3х — 2 3х² — х — 2 = 3(х — 1)(х + 2 / 3) = (х — 1)(3х + 2) Д = 1 — 4·3·( — 2) = 25, √Д = 5 х1 = 6 / 6 = 1 х2 = — 4 / 6 = — 2 / 3.

Каждая сторона квадрата по 3 см, т. К периметр находится по формуле P = а + в + с + d, получаем 12÷4 = 3. S = а², следовательно S = 3² = 9 Ответ : S = 9.

17 хвилин гойдався кожен хлопчик.

Ответ : Пошаговое объяснение : Первоначальная цена составляет 100 % , после снижения , новая цена составила 100 — 15 = 85% от первоначальной цены 1) при первоначальной цене 58000 руб. , цена после снижения составила 58000 * 85% = 58000 * 85 : 100 = ..

357 753 537 573 375 735.

1)76•38 = 2888(литров) — всего Дальше делии на данные числа, 120, 480 и т. Д.

76 / 38 = 2 л сока в одном пакете 120 / 2 = 60 пакетов потребуется для 120 литров сока 240 : 2 = 120 пакетов потребуется для 240 литров сока 480 : 2 = 240 пакетов потребуется для 480 литров сока.

20 63 64 нельзя и 0 отрицательным несуществует.

53 числа, если концы не брать в промежуток 54, если брать концы.

Источник

Теоретическая часть

Лабораторная работа №1. Случайные события

«Классическое определение вероятности. Основные формулы комбинаторики».

Теоретическая часть.

Классическая схема позволяет вычислять вероятности без проведения случайного эксперимента, основываясь лишь на свойстве симметрии возможных исходов испытания, так что нет оснований считать какой-либо из исходов более вероятным, чем другой.

Определение: Вероятностью случайного события А, называется отношение числа m исходов, благоприятствующих событию А, к числу всех равновозможных исходов испытания, составляющих полную группу несовместных событий.

Р(А)=

При непосредственном подсчете вероятностей часто используют формулы комбинаторики. Простейшими из них являются перестановки, сочетания, размещения и разбиения.

Перестановки отличаются друг от друга только порядком входящих в них элементов. Количество перестановок из n элементов:

Пример 1: Сколькими способами можно рассадить 10 человек за круглым столом, если имеет значение только порядок соседей.

Отметим, что вращение людей вокруг стола не меняет их взаимного расположения, поскольку соседи справа и слева остаются прежними. Если место за столом уникально, то существует 10! Способов рассадить людей за столом. Существует 10 вращений вокруг стола, поэтому делим на 10 и получаем 9! Способов рассадить людей за круглым столом, если значение имеет только порядок соседей.

Пусть М – множество, состоящее из n элементов.

Размещением из n элементов по m или упорядоченной (n,m)– выборкой, называется любой кортеж, состоящий из m, попарно различных элементов множества М.

Число размещений из n по m элементов:

Пример 2: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9, если все цифры различны.

Сочетанием из n элементов по m или неупорядоченной (n,m)­­– выборкой, называется любое подмножество множества M, состоящее из m элементов.

Надо заметить, что количество сочетаний отличается от числа размещений количеством перестановок каждого сочетания, то есть

Пример 3: Сколько существует вариантов выбора 5 карт трефовой масти из колоды, состоящей из 54 карт.

В колоде имеется 13 треф, из которых выбирается 5, поэтому

Пусть множество М разбито на k таких различных типов, что имеется n₁ неразличимых объектов типа 1, n₂ неразличимых объектов типа 2, и, вообще, n_i неразличимых объектов типа i (i=1,2,3,…,k), тогда количество различных размещений элементов множества:

Пример 4: Сколькими способами можно расставить на полке 12 книг, из которых 4 одинаковых учебника по математике, 6 одинаковых по информатике, 2 одинаковых по химии.

Если трактовать повторения как возвращения объекта во множество М и повторное его использование, то возникает идея размещений и сочетаний с повторениями. Их количество можно вычислить по формулам:

– количество размещений из n элементов по m с повторениями.

– количество сочетаний из n элементов по m с повторениями.

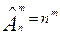
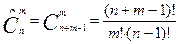
Пример 5: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9.

Так как нет ограничения на повторение цифр, то существует

Теорема: Если необходимо выбрать хотя бы по одному объекту из n по m с повторением, то количество различных сочетаний равно

Пример 6: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков.

Поскольку 12 пончиков выбираются из 10 видов с повторениями, то

Пример 7: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков, если необходимо выбрать хотя бы по одному пончику каждого вида .

Поскольку 12 пончиков выбираются из 10 видов с повторениями, то

Пример 8: Найдем количество различных решений уравнения

, где каждое слагаемое в левой части – неотрицательное число.

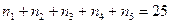
Это эквивалентно вопросу о том, сколько существует выборок вида

, где имеется объектов типа и

, но количество таких выборок — это количество различных сочетаний из 25 элементов по 5 элементов с повторениями. Итак, существуют

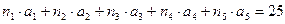
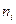
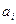
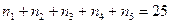
В среде MathCad нет встроенных функций для подсчета количества способов выбора объектов, поэтому необходимо воспользоваться возможностью программирования.

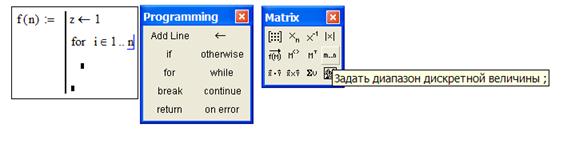
Чтобы создать программный модуль:

1. Введите выражение, которое будет находится слева от знака присваивания (имя функции);

2. Вызовите на экран панель Programming (программирование);

3. Нажмите на кнопку Add line[1] необходимое число раз;

4. В появившиеся местозаполнители введите необходимый программный код.

Для подсчета факториала необходимо организовать цикл. В среде MathCad это можно сделать с помощью оператора for и ранжирванной переменной, которая пробегает некоторое множество значений.

Фрагмент документа MathCad для подсчета факториала приведен ниже.

После того как программный модуль полностью определен и ни один из местозаполнителей ни остался пустым, функция может использоваться обычным образом.

Пример решения задачи на подсчет вероятности в среде МathCad:

Источник