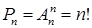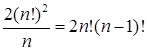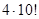Сколькими способами можно рассадить трех учеников за круглым столом с тремя стульями

Сколькими способами можно рассадить трех учеников за круглым столом с тремя стульями

Вопрос по математике:

Сколькими способами можно рассадить трех учеников за круглым столом с тремя стульями

Ответы и объяснения 1

-на первый стул можно посадить одного из ТРЕХ человек,
-на второй стул можно посадить одного из ДВУХ оставшихся,
=на третий стул можно посадить ОДНОГО оставшегося
ПОЛУЧАЕМ:
3*2*1=6 вариантов (по правилу произведения)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник

Волжский класс

Боковая колонка

Рубрики

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Ноябрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
« Окт
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

6 класс. Математика. Никольский. Учебник. Ответы к стр. 35

Отношения, пропорции, проценты
Задачи на перебор всех возможных вариантов

Ответы к стр. 35

152. У круглого стола поставили четыре стула. Сколькими способами можно рассадить на эти стулья:
а) четырёх детей; б) трёх детей; в) двух детей?

а) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, четвёртый ребёнок может сесть только на один оставшийся стул , то есть имеется 4 • 3 • 2 • 1 = 24 возможных способа рассадить четырёх детей на стулья.

б) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, один стул остаётся свободным, то есть имеется 4 • 3 • 2 = 24 возможных способа рассадить трёх детей на стулья.

в) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, два стула остаются свободными, то есть имеется 4 • 3 = 12 возможных способа рассадить двух детей на стулья.

153. Мальчика и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, а с другой стороны — находиться пустой стул.
Мальчик может сесть на любой из четырёх стульев, первая девочка может сесть на любой из двух оставшихся стульев рядом с мальчиком (но только не напротив него), вторая девочка может сесть на оставшийся стул рядом с мальчиком (но только не напротив него), то есть имеется 4 • 2 • 1 = 8 возможных способов рассадить детей.

154. Двух мальчиков и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, и с другой стороны тоже сидеть мальчик.
Первая девочка может сесть на любой из четырёх стульев, первый мальчик может сесть на любой из двух оставшихся стульев рядом с девочкой (но только не напротив неё), вторая девочка может сесть на стул рядом с мальчиком и напротив первой девочки, второй мальчик может сесть на оставшийся стул, то есть имеется 4 • 2 • 1 • 1 = 8 возможных способов рассадить детей.

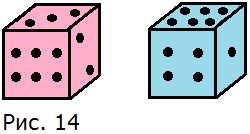
155. Бросили два игральных кубика. На первом выпало 3 очка, на втором — 6 очков. (рис. 14). Сколькими разными способами может выпасть сумма в 9 очков? Сколькими различными способами могут выпасть очки на этих кубиках?

Сумму 9 можно получить: 3 + 6 и 4 + 5. На первом кубике может выпасть любое из четырёх чисел (3, 4, 5 или 6), на втором кубике может выпасть только одно число, дополняющее число, выпавшее на первом кубике до суммы, равной 9 (3 + 6, 6 + 3, 4 + 5, 5 + 4), то есть имеется 4 • 1 = 4 возможных способа получить сумму в 9 очков.

На первом кубике может выпасть любое из шести чисел, на втором кубике может также выпасть любое из шести чисел, то есть имеется 6 • 6 = 36 возможных способов.

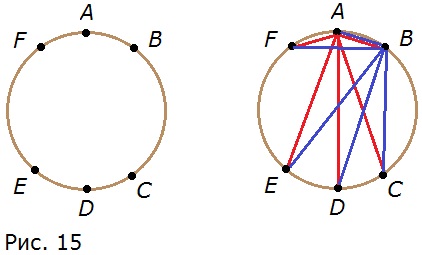
156. а) На окружности отметили 6 точек (рис. 15). Сколько получится отрезков, если соединить каждую точку с каждой?

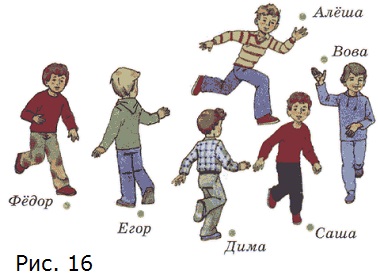
б) Встретились шесть друзей (рис. 16), каждый пожал руку каждому. Сколько было рукопожатий?

а) Из точки А выходит 5 отрезков. Из точки В выходит тоже 5 отрезков, но отрезок ВА — это тот же отрезок АВ. Если продолжить построение отрезков, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 отрезков.

б) Алёша пожал руку Фёдору, Егору, Диме, Саше и Вове — всего 5 рукопожатий. Фёдор пожал руку Алёше, Егору, Диме, Саше и Вове — всего тоже 5 рукопожатий. Но рукопожатие Алёша-Фёдор и Фёдор-Алёша — это одно рукопожатие. Если продолжить рассматривать рукопожатия, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 рукопожатий .

157. Восемь друзей решили провести турнир по шашкам так, чтобы каждый сыграл с каждым одну партию. Сколько партий будет сыграно?

Всего 8 друзей, значит, каждый сыграет одну партию с каждым из семи оставшихся друзей. Но, например, если Витя сыграет с Лёшей и Лёша сыграет с Витей — это одна и та же партия. Если продолжить рассматривать количество сыгранных партий, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (8 • 7) : 2 = 28 партий.

Источник

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .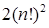

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .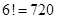

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .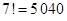

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .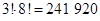

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .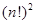

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .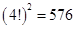

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .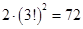

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник

Сколькими способами можно рассадить трех учеников за круглым столом с тремя стульями

За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Пусть первой за стол сядет девочка, рядом с ней есть два места, на каждое из которых может сесть 8 человек, из которых только одна девочка. Таким образом вероятность, что девочки будут сидеть рядом равна

Приведём другое решение (перестановки).

Число способов рассадить 9 человек по девяти стульям равно Благоприятным является случай, когда на «первом» стуле сидит «первая» девочка, на соседнем справа сидит «вторая» девочка, а на остальных семи стульях произвольным образом рассажены мальчики. Поскольку выбрать «первую» девочку можно двумя способами, количество таких исходов равно А так как «первым» стулом может быть любой из девяти стульев (стулья стоят по кругу), количество благоприятных исходов нужно умножить на 9. Таким образом, вероятность того, что обе девочки будут сидеть рядом, равна

Приведём другое решение (круговые перестановки).

Напомним, что число способов, которыми можно расположить n различных объектов по n расположенным по кругу местам равно (n − 1)! Поэтому посадить за круглым столом 9 детей можно 8! способами. Объединим двух девочек в пару, это можно сделать двумя способами; рассадить по кругу 7 мальчиков и эту неделимую пару можно 7! способами. Тем самым, посадить детей требуемым образом можно 2 · 7! способами, поэтому искомая вероятность равна

Рассуждая аналогично, получим, что в общем случае для n девочек и m мальчиков, сидящих девочки с девочками, а мальчики с мальчиками, количество способов занять места за круговым столом равно n!m!, а вероятность случайной рассадки требуемым образом равна

Источник