Сколькими способами можно рассадить четверых детей

Волжский класс

Боковая колонка

Рубрики

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Ноябрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
« Окт
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

6 класс. Математика. Никольский. Учебник. Ответы к стр. 35

Отношения, пропорции, проценты
Задачи на перебор всех возможных вариантов

Ответы к стр. 35

152. У круглого стола поставили четыре стула. Сколькими способами можно рассадить на эти стулья:
а) четырёх детей; б) трёх детей; в) двух детей?

а) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, четвёртый ребёнок может сесть только на один оставшийся стул , то есть имеется 4 • 3 • 2 • 1 = 24 возможных способа рассадить четырёх детей на стулья.

б) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, один стул остаётся свободным, то есть имеется 4 • 3 • 2 = 24 возможных способа рассадить трёх детей на стулья.

в) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, два стула остаются свободными, то есть имеется 4 • 3 = 12 возможных способа рассадить двух детей на стулья.

153. Мальчика и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, а с другой стороны — находиться пустой стул.
Мальчик может сесть на любой из четырёх стульев, первая девочка может сесть на любой из двух оставшихся стульев рядом с мальчиком (но только не напротив него), вторая девочка может сесть на оставшийся стул рядом с мальчиком (но только не напротив него), то есть имеется 4 • 2 • 1 = 8 возможных способов рассадить детей.

154. Двух мальчиков и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, и с другой стороны тоже сидеть мальчик.
Первая девочка может сесть на любой из четырёх стульев, первый мальчик может сесть на любой из двух оставшихся стульев рядом с девочкой (но только не напротив неё), вторая девочка может сесть на стул рядом с мальчиком и напротив первой девочки, второй мальчик может сесть на оставшийся стул, то есть имеется 4 • 2 • 1 • 1 = 8 возможных способов рассадить детей.

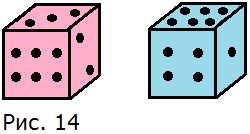
155. Бросили два игральных кубика. На первом выпало 3 очка, на втором — 6 очков. (рис. 14). Сколькими разными способами может выпасть сумма в 9 очков? Сколькими различными способами могут выпасть очки на этих кубиках?

Сумму 9 можно получить: 3 + 6 и 4 + 5. На первом кубике может выпасть любое из четырёх чисел (3, 4, 5 или 6), на втором кубике может выпасть только одно число, дополняющее число, выпавшее на первом кубике до суммы, равной 9 (3 + 6, 6 + 3, 4 + 5, 5 + 4), то есть имеется 4 • 1 = 4 возможных способа получить сумму в 9 очков.

На первом кубике может выпасть любое из шести чисел, на втором кубике может также выпасть любое из шести чисел, то есть имеется 6 • 6 = 36 возможных способов.

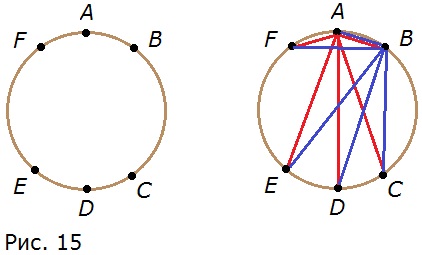
156. а) На окружности отметили 6 точек (рис. 15). Сколько получится отрезков, если соединить каждую точку с каждой?

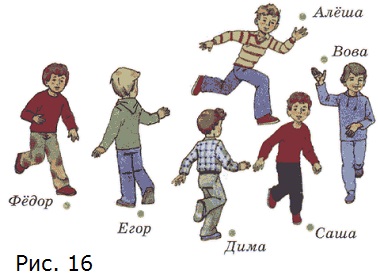
б) Встретились шесть друзей (рис. 16), каждый пожал руку каждому. Сколько было рукопожатий?

а) Из точки А выходит 5 отрезков. Из точки В выходит тоже 5 отрезков, но отрезок ВА — это тот же отрезок АВ. Если продолжить построение отрезков, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 отрезков.

б) Алёша пожал руку Фёдору, Егору, Диме, Саше и Вове — всего 5 рукопожатий. Фёдор пожал руку Алёше, Егору, Диме, Саше и Вове — всего тоже 5 рукопожатий. Но рукопожатие Алёша-Фёдор и Фёдор-Алёша — это одно рукопожатие. Если продолжить рассматривать рукопожатия, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 рукопожатий .

157. Восемь друзей решили провести турнир по шашкам так, чтобы каждый сыграл с каждым одну партию. Сколько партий будет сыграно?

Всего 8 друзей, значит, каждый сыграет одну партию с каждым из семи оставшихся друзей. Но, например, если Витя сыграет с Лёшей и Лёша сыграет с Витей — это одна и та же партия. Если продолжить рассматривать количество сыгранных партий, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (8 • 7) : 2 = 28 партий.

Источник

Волжский класс

Боковая колонка

Рубрики

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Ноябрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
« Окт
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

6 класс. Математика. Никольский. Учебник. Ответы к стр. 35

Отношения, пропорции, проценты
Задачи на перебор всех возможных вариантов

Ответы к стр. 35

152. У круглого стола поставили четыре стула. Сколькими способами можно рассадить на эти стулья:
а) четырёх детей; б) трёх детей; в) двух детей?

а) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, четвёртый ребёнок может сесть только на один оставшийся стул , то есть имеется 4 • 3 • 2 • 1 = 24 возможных способа рассадить четырёх детей на стулья.

б) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, один стул остаётся свободным, то есть имеется 4 • 3 • 2 = 24 возможных способа рассадить трёх детей на стулья.

в) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, два стула остаются свободными, то есть имеется 4 • 3 = 12 возможных способа рассадить двух детей на стулья.

153. Мальчика и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, а с другой стороны — находиться пустой стул.
Мальчик может сесть на любой из четырёх стульев, первая девочка может сесть на любой из двух оставшихся стульев рядом с мальчиком (но только не напротив него), вторая девочка может сесть на оставшийся стул рядом с мальчиком (но только не напротив него), то есть имеется 4 • 2 • 1 = 8 возможных способов рассадить детей.

154. Двух мальчиков и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, и с другой стороны тоже сидеть мальчик.
Первая девочка может сесть на любой из четырёх стульев, первый мальчик может сесть на любой из двух оставшихся стульев рядом с девочкой (но только не напротив неё), вторая девочка может сесть на стул рядом с мальчиком и напротив первой девочки, второй мальчик может сесть на оставшийся стул, то есть имеется 4 • 2 • 1 • 1 = 8 возможных способов рассадить детей.

155. Бросили два игральных кубика. На первом выпало 3 очка, на втором — 6 очков. (рис. 14). Сколькими разными способами может выпасть сумма в 9 очков? Сколькими различными способами могут выпасть очки на этих кубиках?

Сумму 9 можно получить: 3 + 6 и 4 + 5. На первом кубике может выпасть любое из четырёх чисел (3, 4, 5 или 6), на втором кубике может выпасть только одно число, дополняющее число, выпавшее на первом кубике до суммы, равной 9 (3 + 6, 6 + 3, 4 + 5, 5 + 4), то есть имеется 4 • 1 = 4 возможных способа получить сумму в 9 очков.

На первом кубике может выпасть любое из шести чисел, на втором кубике может также выпасть любое из шести чисел, то есть имеется 6 • 6 = 36 возможных способов.

156. а) На окружности отметили 6 точек (рис. 15). Сколько получится отрезков, если соединить каждую точку с каждой?

б) Встретились шесть друзей (рис. 16), каждый пожал руку каждому. Сколько было рукопожатий?

а) Из точки А выходит 5 отрезков. Из точки В выходит тоже 5 отрезков, но отрезок ВА — это тот же отрезок АВ. Если продолжить построение отрезков, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 отрезков.

б) Алёша пожал руку Фёдору, Егору, Диме, Саше и Вове — всего 5 рукопожатий. Фёдор пожал руку Алёше, Егору, Диме, Саше и Вове — всего тоже 5 рукопожатий. Но рукопожатие Алёша-Фёдор и Фёдор-Алёша — это одно рукопожатие. Если продолжить рассматривать рукопожатия, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 рукопожатий .

157. Восемь друзей решили провести турнир по шашкам так, чтобы каждый сыграл с каждым одну партию. Сколько партий будет сыграно?

Всего 8 друзей, значит, каждый сыграет одну партию с каждым из семи оставшихся друзей. Но, например, если Витя сыграет с Лёшей и Лёша сыграет с Витей — это одна и та же партия. Если продолжить рассматривать количество сыгранных партий, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (8 • 7) : 2 = 28 партий.

Источник

Сколькими способами можно рассадить четверых детей на четырёх стульях в столовой детского сада?

Математика | 5 — 9 классы

Сколькими способами можно рассадить четверых детей на четырёх стульях в столовой детского сада.

На первое место претендуют всего 4 человек, на второе место — 3 человека, т.

К. один человек уже занял свое место, на второе место — 2 и на первое место 1.

По правилу произведения, всего рассадить можно 4 * 3 * 2 * 1 = 4!

Сколькими способами можно рассадить в ряд на 3 стула 3 учеников?

Сколькими способами можно рассадить в ряд на 3 стула 3 учеников.

В группе детского сада 12 детей?

В группе детского сада 12 детей.

Сколькими способами их можно поставить в колонну парами ?

К полднику в детском саду на четырёхместный стол поставили сок, молоко, какао и компот?

К полднику в детском саду на четырёхместный стол поставили сок, молоко, какао и компот.

Сколькими способами четверо детей могут выбрать себе один из напитков?

Помогите пожалуйста?

Задача : В детском саду было четверо детей.

На полдник за четырехместный стол поставили : сок ; молоко ; какао и компот.

Какими способами могут выбрать напитки дети?

Семь детей семь стульев сколько вариантов что бы их рассадить?

Семь детей семь стульев сколько вариантов что бы их рассадить.

Сколькими способами можно рассадить 3 стула, трех людей?

Сколькими способами можно рассадить 3 стула, трех людей?

Сколькими способами можно рассадить четверых детей на четырех стульях в столовой детского сада?

Сколькими способами можно рассадить четверых детей на четырех стульях в столовой детского сада.

У круглого стола поставили четыре стула?

У круглого стола поставили четыре стула.

Сколькими способами можно рассадить на эти стулья трёх детей.

В школьную столовую привезли 8 десятков яиц, а в столовую детского сада — на 3 десятка меньше?

В школьную столовую привезли 8 десятков яиц, а в столовую детского сада — на 3 десятка меньше.

Сколько всего яиц привезли в столовую детского сада?

В одном детском саду а детей а в другом на b детей больше?

В одном детском саду а детей а в другом на b детей больше.

Сколько всего детей в другом детском саду?

На этой странице сайта размещен вопрос Сколькими способами можно рассадить четверых детей на четырёх стульях в столовой детского сада? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

3 — е задание. Ответ 24 см, 32 см, 52см.

1)выражение : 82 + 18 ; 7 + 29 значения выражения : 100 ; 36 2)выражение : 35 — 12 ; 90 — 15 значение выражения : 23 ; 75 3)выражение : 56 : 7 ; 63 : 9 значение выражения : 8 ; 7 4) выражение : 9 * 1 ; 7 * 3 значение выражения : 9 ; 21.

1) 20 + 14 = 34 кг — во втором ящике 2) 20 + 34 = 54 кг — в двух ящиках вместе 3) 54 : 6 = 9 кг яблок — в одном ящике.

Вот, на фотографии все видно.

5 насосов понадобится на 21 акулу.

1) 2136 + 1000 = 3136 3136 / 16 = 196 2) 15 * 5 = 75 55350 / 75 = 738.

(1, 05 + ( — 1 1 / 20)) + 1 : 1 1 / 29 = (1, 05 — 1, 05) + 1 : 30 / 29 = 0 + 29 / 30 = 29 / 30 ответ : 29 / 30.

Изначально в 1 ящике было 5x мандаринов, а во втором x мандаринов, когда из 1 ящика взяли 25 кг, а во второй положили 15кг, то в 1 ящике стало 5x — 25 мандаринов , а во втором x + 15 мандаринов, т. К. в обоих ящиках стало поровну, то получаем следую..

Площадь треугольника по формуле Герона : a = 36 см, b = 25 см, c = 29 см р — полупериметр треугольника p = 45 SΔ = 360 см² формула площади треугольника, если известна сторона и высота проведенная к этой стороне : 1. см 2. см 3. см.

Источник