Сколькими способами можно рассадить 3 учащихся за круглым столом с 3 стульями

Сколькими способами можно рассадить 3 учащихся за круглым столом с 3 стульями

Вопрос по математике:

Сколькими способами можно рассадить трех учеников за круглым столом с тремя стульями

Ответы и объяснения 1

-на первый стул можно посадить одного из ТРЕХ человек,
-на второй стул можно посадить одного из ДВУХ оставшихся,
=на третий стул можно посадить ОДНОГО оставшегося
ПОЛУЧАЕМ:
3*2*1=6 вариантов (по правилу произведения)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник

Волжский класс

Боковая колонка

Рубрики

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Ноябрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
« Окт
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

6 класс. Математика. Никольский. Учебник. Ответы к стр. 35

Отношения, пропорции, проценты
Задачи на перебор всех возможных вариантов

Ответы к стр. 35

152. У круглого стола поставили четыре стула. Сколькими способами можно рассадить на эти стулья:
а) четырёх детей; б) трёх детей; в) двух детей?

а) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, четвёртый ребёнок может сесть только на один оставшийся стул , то есть имеется 4 • 3 • 2 • 1 = 24 возможных способа рассадить четырёх детей на стулья.

б) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, один стул остаётся свободным, то есть имеется 4 • 3 • 2 = 24 возможных способа рассадить трёх детей на стулья.

в) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, два стула остаются свободными, то есть имеется 4 • 3 = 12 возможных способа рассадить двух детей на стулья.

153. Мальчика и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, а с другой стороны — находиться пустой стул.
Мальчик может сесть на любой из четырёх стульев, первая девочка может сесть на любой из двух оставшихся стульев рядом с мальчиком (но только не напротив него), вторая девочка может сесть на оставшийся стул рядом с мальчиком (но только не напротив него), то есть имеется 4 • 2 • 1 = 8 возможных способов рассадить детей.

154. Двух мальчиков и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, и с другой стороны тоже сидеть мальчик.
Первая девочка может сесть на любой из четырёх стульев, первый мальчик может сесть на любой из двух оставшихся стульев рядом с девочкой (но только не напротив неё), вторая девочка может сесть на стул рядом с мальчиком и напротив первой девочки, второй мальчик может сесть на оставшийся стул, то есть имеется 4 • 2 • 1 • 1 = 8 возможных способов рассадить детей.

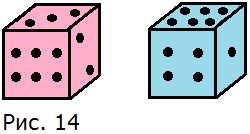
155. Бросили два игральных кубика. На первом выпало 3 очка, на втором — 6 очков. (рис. 14). Сколькими разными способами может выпасть сумма в 9 очков? Сколькими различными способами могут выпасть очки на этих кубиках?

Сумму 9 можно получить: 3 + 6 и 4 + 5. На первом кубике может выпасть любое из четырёх чисел (3, 4, 5 или 6), на втором кубике может выпасть только одно число, дополняющее число, выпавшее на первом кубике до суммы, равной 9 (3 + 6, 6 + 3, 4 + 5, 5 + 4), то есть имеется 4 • 1 = 4 возможных способа получить сумму в 9 очков.

На первом кубике может выпасть любое из шести чисел, на втором кубике может также выпасть любое из шести чисел, то есть имеется 6 • 6 = 36 возможных способов.

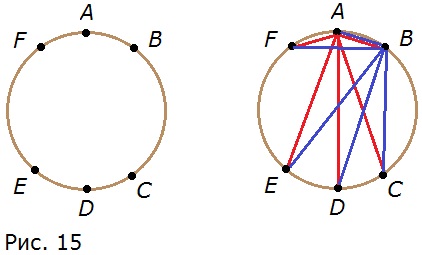
156. а) На окружности отметили 6 точек (рис. 15). Сколько получится отрезков, если соединить каждую точку с каждой?

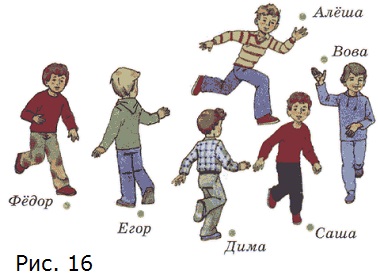
б) Встретились шесть друзей (рис. 16), каждый пожал руку каждому. Сколько было рукопожатий?

а) Из точки А выходит 5 отрезков. Из точки В выходит тоже 5 отрезков, но отрезок ВА — это тот же отрезок АВ. Если продолжить построение отрезков, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 отрезков.

б) Алёша пожал руку Фёдору, Егору, Диме, Саше и Вове — всего 5 рукопожатий. Фёдор пожал руку Алёше, Егору, Диме, Саше и Вове — всего тоже 5 рукопожатий. Но рукопожатие Алёша-Фёдор и Фёдор-Алёша — это одно рукопожатие. Если продолжить рассматривать рукопожатия, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 рукопожатий .

157. Восемь друзей решили провести турнир по шашкам так, чтобы каждый сыграл с каждым одну партию. Сколько партий будет сыграно?

Всего 8 друзей, значит, каждый сыграет одну партию с каждым из семи оставшихся друзей. Но, например, если Витя сыграет с Лёшей и Лёша сыграет с Витей — это одна и та же партия. Если продолжить рассматривать количество сыгранных партий, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (8 • 7) : 2 = 28 партий.

Источник

Волжский класс

Боковая колонка

Рубрики

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Ноябрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
« Окт
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

6 класс. Математика. Никольский. Учебник. Ответы к стр. 35

Отношения, пропорции, проценты
Задачи на перебор всех возможных вариантов

Ответы к стр. 35

152. У круглого стола поставили четыре стула. Сколькими способами можно рассадить на эти стулья:
а) четырёх детей; б) трёх детей; в) двух детей?

а) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, четвёртый ребёнок может сесть только на один оставшийся стул , то есть имеется 4 • 3 • 2 • 1 = 24 возможных способа рассадить четырёх детей на стулья.

б) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, один стул остаётся свободным, то есть имеется 4 • 3 • 2 = 24 возможных способа рассадить трёх детей на стулья.

в) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, два стула остаются свободными, то есть имеется 4 • 3 = 12 возможных способа рассадить двух детей на стулья.

153. Мальчика и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, а с другой стороны — находиться пустой стул.
Мальчик может сесть на любой из четырёх стульев, первая девочка может сесть на любой из двух оставшихся стульев рядом с мальчиком (но только не напротив него), вторая девочка может сесть на оставшийся стул рядом с мальчиком (но только не напротив него), то есть имеется 4 • 2 • 1 = 8 возможных способов рассадить детей.

154. Двух мальчиков и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?

Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, и с другой стороны тоже сидеть мальчик.
Первая девочка может сесть на любой из четырёх стульев, первый мальчик может сесть на любой из двух оставшихся стульев рядом с девочкой (но только не напротив неё), вторая девочка может сесть на стул рядом с мальчиком и напротив первой девочки, второй мальчик может сесть на оставшийся стул, то есть имеется 4 • 2 • 1 • 1 = 8 возможных способов рассадить детей.

155. Бросили два игральных кубика. На первом выпало 3 очка, на втором — 6 очков. (рис. 14). Сколькими разными способами может выпасть сумма в 9 очков? Сколькими различными способами могут выпасть очки на этих кубиках?

Сумму 9 можно получить: 3 + 6 и 4 + 5. На первом кубике может выпасть любое из четырёх чисел (3, 4, 5 или 6), на втором кубике может выпасть только одно число, дополняющее число, выпавшее на первом кубике до суммы, равной 9 (3 + 6, 6 + 3, 4 + 5, 5 + 4), то есть имеется 4 • 1 = 4 возможных способа получить сумму в 9 очков.

На первом кубике может выпасть любое из шести чисел, на втором кубике может также выпасть любое из шести чисел, то есть имеется 6 • 6 = 36 возможных способов.

156. а) На окружности отметили 6 точек (рис. 15). Сколько получится отрезков, если соединить каждую точку с каждой?

б) Встретились шесть друзей (рис. 16), каждый пожал руку каждому. Сколько было рукопожатий?

а) Из точки А выходит 5 отрезков. Из точки В выходит тоже 5 отрезков, но отрезок ВА — это тот же отрезок АВ. Если продолжить построение отрезков, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 отрезков.

б) Алёша пожал руку Фёдору, Егору, Диме, Саше и Вове — всего 5 рукопожатий. Фёдор пожал руку Алёше, Егору, Диме, Саше и Вове — всего тоже 5 рукопожатий. Но рукопожатие Алёша-Фёдор и Фёдор-Алёша — это одно рукопожатие. Если продолжить рассматривать рукопожатия, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 рукопожатий .

157. Восемь друзей решили провести турнир по шашкам так, чтобы каждый сыграл с каждым одну партию. Сколько партий будет сыграно?

Всего 8 друзей, значит, каждый сыграет одну партию с каждым из семи оставшихся друзей. Но, например, если Витя сыграет с Лёшей и Лёша сыграет с Витей — это одна и та же партия. Если продолжить рассматривать количество сыгранных партий, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (8 • 7) : 2 = 28 партий.

Источник

Сколькими способами можно рассадить 3 учащихся за круглым столом с 3 стульями

В школьном курсе понятие «круговые перестановки» встречается в 7 классе в учебнике по алгебре в разделе «Для тех, кому интересно» [3].

В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить в ряд, или, как говорят математики, упорядочить, все элементы некоторого множества.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Получаемые при этом упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них элементов, называют перестановками без повторений из п элементовили «круговыми перестановками».

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют “сочетания”. В ХII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из п слогов. Как научная дисциплина, комбинаторика сформировалась в Х V II в. В книге “Теория и практика арифметики” (1656 г.) французский автор Андре Таке также посвящает сочетаниям и перестановкам целую главу.

Б. Паскаль в “Трактате об арифметическом треугольнике” и в “Трактате о числовых порядках” (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин “комбинаторика” стал употребляться после опубликования Лейбницем в 1665 г. работы “Рассуждение о комбинаторном искусстве”, в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги “Аг s соп j ес t ап d i” (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в ХIХ в [4].

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения. При решении задач на перестановки используется правило умножения.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Рассмотрим задачу: В турнире четверо участников. Сколькими способами могут быть распределены места между ними?

Будем рассуждать в соответствии с правилом умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье любой из двух оставшихся, а на четвертом месте останется последний участник. Значит, места между участниками могут быть распределены 4 ۰ 3 ۰ 2 ۰ 1 = 24 способами. Решив задачу, мы фактически подсчитали число перестановок для множества из четырех элементов. Рассуждая точно так же, можно показать, что для множества из пяти элементов число перестановок равно 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1, а для множества из десяти элементов это число равно 10 ۰ 9 ۰ 8 ۰ 7 ۰ б ۰ 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1.

Вообще если множество содержит п элементов, то число перестановок равно произведению п(п – 1)(п – 2) ۰…۰ 2 ۰ 1. Множители в этом произведении можно записать в обратном порядке: 1 ۰ 2 ۰ . ۰ (п – 2)(п – 1)п.

Такие произведения бывают очень длинными и часто выражаются огромными числами. Однако в математике есть специальный символ для их обозначения. Произведение всех натуральных чисел от 1 до п обозначают п! (читают: «п факториал»). Значение выражения п! можно найти для любого натурального числа п (при этом считают, что 1! = 1).

Факториалы растут удивительно быстро. Можно понаблюдать за их изменением, рассмотрев таблицу, в которой приведены факториалы чисел от 1 до 10:

Источник