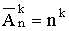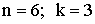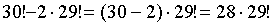Сколькими способами можно распределить поровну 12 различных учебников между четырьмя студентами

Сколькими способами можно распределить 12 разных книг между четырьмя учащимися если можно, подробное объяснение?

Алгебра | 10 — 11 классы

Сколькими способами можно распределить 12 разных книг между четырьмя учащимися если можно, подробное объяснение.

На мой взгляд, тут важен и порядок элемента и сам выбор элемента, т.

Е. это сводится к размещению.

Но вычисляя по этой формуле, ответ не тот.

Тут будем использовать комбинаторику размещения.

Книги разные, поэтому разница будет если их мы меняем между учащимися.

A(m — вверху, n — снизу) = n!

\ 8! (сокращаем) = 9 х 10 х 11 х 12 = 11880.

1. В классе 30 учащихся?

1. В классе 30 учащихся.

Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории, литературе, русскому и английскому языкам?

2. В библиотеке Кате предложили на выбор из новых поступлений 10 книг и 4 журнала.

Сколькими способами она может выбрать из них 3 книги и 2 журнала?

3. Сколькими способами 8 учащихся могут встать в очередь в школьном буфете?

Число размещений 5 элементов по 3 равно?

Число размещений 5 элементов по 3 равно.

Число размещений из n элементов по четыре в 14 раз больше числа размещений из n — 2 элементов по три?

Число размещений из n элементов по четыре в 14 раз больше числа размещений из n — 2 элементов по три.

Даны элементы a, b, c, d?

Даны элементы a, b, c, d.

Из этих элементов составить группы перестановок.

Вычислите их количество.

Помогите пожалуйста ?

Сколькими способами можно расположить 17 книг на двух полках, если на одной полке можно разместить 7 книг , а на второй 10 , и порядок расположения книг на полках важен.

Из восьми учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде , Сколькими способами это можно сделать выбор?

Из восьми учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде , Сколькими способами это можно сделать выбор?

Ребят можно по подробней (максимально).

Из 8 книг и 5 журналов необходимо выбрать 3 книги и 2 журнала ?

Из 8 книг и 5 журналов необходимо выбрать 3 книги и 2 журнала .

Сколькими способами это можно сделать этот выбор?

Сколькими способами 6 человек смогут разместиться на 6 местах зрительного зала?

Сколькими способами 6 человек смогут разместиться на 6 местах зрительного зала?

Тема : «Элементы комбинаторики».

Просьба отвечать пользователей, хорошо разбирающихся в алгебре.

Пожалуйста, напишите подробное решение или объяснение, чтобы понять.

Сколькими способами можно распредилить 12 различных книг можно чертырьмя учащимися?

Сколькими способами можно распредилить 12 различных книг можно чертырьмя учащимися?

На полке стоит 12 разных книг?

На полке стоит 12 разных книг.

Сколькими способами из них можно выбрать 9 книг?

На этой странице сайта, в категории Алгебра размещен ответ на вопрос Сколькими способами можно распределить 12 разных книг между четырьмя учащимися если можно, подробное объяснение?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Источник

Сколькими способами можно распределить поровну 12 различных учебников между четырьмя студентами

Вопрос по математике:

Сколькими способами можно разделить 12 учебников между четырьмя студентами

Ответы и объяснения 1

Общее число способов вычисляется по формуле:

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник

Сколькими способами можно распределить экзаменационные вопросы между студентами поровну?

Сколькими способами можно распределить книги поровну между 2 людьми ?
Имеется 7 экземпляров одной книги, 8 – другой и 9 – третьей. Сколькими способами можно.

Сколькими способами можно распределить 3 путёвки между 5 студентами?
Помогите решить вот такую задачу) Сколькими способами можно распределить 3 путёвки между 5.

Сколькими способами можно распределить темы между студентами, чтобы каждая тема оказалась выученной
К экзамену нужно выучить 11 тем . Шесть студентов договорились , что каждый выучит по две темы и.

Сколькими способами можно разделить 36 одинаковых тетрадей между шестью студентами?
Всем привет! Требуется помощь. Уже как-то позабыл как это решать. Сколькими способами можно.

Решение

Сколькими способами можно распределить 6 заданий между 3 работниками
Требуется выполнить 6 заданий. Задания могут выполняться независимо одно от другого. Имеется 3.

Сколькими способами можно распределить между восемью токарями задание по изготовлению
Прошу помочь, сломал всю голову. Сколькими способами можно распределить между восемью токарями.

Сколькими способами можно распределить между ними имеющиеся рабочие места?
В центр занятости обратилось 7 человек, имеющих одинаковые потенциальные возможности. Для них есть.

Сколькими способами можно распределить между этажами число людей, которые вышли на каждом этаже?
Лифт шестиэтажного дома поднимает с первого этажа 10 человек.Сколькими способами можно распределить.

Источник

Разделить 12 предметов на 4 человека

Пусть есть 12 предметов, к примеру книг.
нужно разделить их на 4 человека. При этом человеку может ничего не достаться и может достаться все, т.е возможен вариант
0-0-0-12

сколькими способами можно так разделить?
и решение пож

сам только перебирать додумался, но что-то слишком много выходит.
вроде ни к размещению, ни к сочетанию не относиться, не знаю

Как разделить набор предметов поровну
2 друга собрались в поход,собрали и взвесили все вещи. Как им разделить набор предметов.

Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок
Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок? Я нашла формулу для.

Известна масса каждого из 12 предметов, определить общую массу всего набора предметов
известна масса каждого из 12 предметов определить общую массу всего набора предметов ?

Известна масса каждого из 12 предметов. Определить общую массу всего набора предметов
Известна масса каждого из 12 предметов. Определить общую массу всего набора предметов.

Решение

это классическая задача расположения 12 шариков по 4 ящикам при том, что и то, и другое различимо (судя по условию — люди точно разные. Ну раз книги — значит, тоже).

Получается. у нас 4 человека.
Каждый объект (книга) у нас может случайно «выбрать» любого человека. Перенумеруйте мысленно людей и присвойте книгам номера, кому они достались.
Получатся варианты типа:
111111111111 (все книги достались первому человеку)
.
123243344421
.
444444444444 (все книги достались последнему человеку)

Поэтому как посчитать общее число вариантов:
4 варианта, кому может достаться 1-я книга, 4 — кому вторая и т.д.. Получается общее число вариантов — число размещений с повторением: А₄ 12 =4 12

Добавлено через 15 часов 29 минут

только число размещений с повторением обычно обозначается А с крышечкой:

Источник

Математика — онлайн помощь

Рассмотрим множество, состоящее из n различных элементов. Требуется выбрать из них какие-нибудь k элементов и расположить эти k элементов в каком-либо порядке. Такие упорядоченные последовательности называются размещениями из n элементов по k элементов (упорядоченные – следовательно, последовательности <1,2>и <2,1>— различные размещения).

Если в последовательности нет одинаковых элементов, то говорят о размещении без повторений. Их количество

Если в последовательности допускается наличие одинаковых элементов, то говорят о размещении с повторениями. Их количество

Любое подмножество (неупорядоченное), состоящее из k элементов, называется сочетанием из n элементов по k элементов.

Различные сочетания отличаются друг от друга только самими входящими в них элементами, порядок их следования безразличен, т.е. по условию задачи подмножества <1,2>и <2,1>не различны (соединены).

Число сочетаний без повторений

.

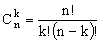
Число сочетаний с повторениями

.

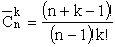
Количество способов переставить элементов в заданном множестве (количество перестановок) вычисляется по формуле

.

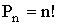
При решении простейших комбинаторных задач можно использовать следующую таблицу, определяющую число множеств, состоящих из k элементов, отбираемых из множества, содержащего n элементов

Выбор	Неупорядоченный	Упорядоченный
Без повтора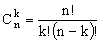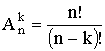
С повтором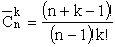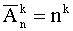

Рассмотрим разницу между сочетаниями, размещениями с повторениями, без повторений на следующих примерах.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПРИМЕР 13.2.1 В коробке 6 шаров, пронумерованных от 1 до 6. Из коробки вынимаются друг за другом 3 шара и в этом же порядке записывают полученные цифры. Сколько трехзначных чисел можно таким образом записать?

Решение: По условию задачи подмножества <1;2;3>и <3;1;2>– различные. Повторов в подмножестве быть не может, так как шары не возвращаются в коробку.

.

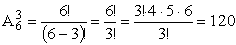
ПРИМЕР 13.2.2. В коробке 6 шаров пронумерованных от 1 до 6. Из коробки вынимаются 3 шара и записывают число в порядке возрастания цифр. Сколько трехзначных чисел можно таким образом записать?

Решение: По условию задачи подмножества <1;2;3>и <3;2;1>дают число 123, т.е. не являются различными.

.

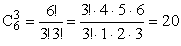
ПРИМЕР 13.2.3. Условие задачи 2.1 (шары возвращаются в коробку)

Решение: .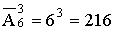

ПРИМЕР 13.2.4. Условие задачи 2.2 (шары возвращаются в коробку)

Решение: .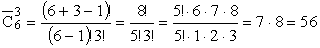

ПРИМЕР 13.2.5. Сколько различных перестановок можно составить из букв слова «комар»?

Решение: .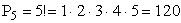

ПРИМЕР 13.2.6. Сколько различных перестановок можно составить из букв слова «задача»?

Решение: Если бы все шесть букв слова были различны, то число перестановок было бы 6! Но буква «а» встречается в данном слове три раза, и перестановки только этих трех букв «а» не дают новых способов расположения букв. Поэтому число перестановок букв слова «задача» будет не 6!, а в 3! раза меньше, то есть .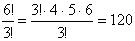

ПРИМЕР 13.2.7. В мастерской имеется материал 5 цветов. Поступил заказ на пошив флагов, состоящих из трех горизонтальных полос разного цвета каждый. Сколько таких различных флагов может сшить мастерская?

.

Решение: Флаги отличаются друг от друга как цветом полос, так и их порядком, поэтому разных флагов можно сделать 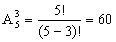штук.

ПРИМЕР 13.2.8. Сколькими способами можно распределить 5 учеников по 3 параллельным классам?

Решение: Составим вспомогательную таблицу

Таким образом, видно, что если для одного ученика существует 3 варианта выбора класса, то для всех 5 учеников существует 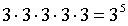способов распределения по классам.

ПРИМЕР 13.2.9. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй том не стояли рядом?

Решение: Произведем рассуждения “от обратного”. Тридцать томов на одной полке можно разместить 30! способами.

.

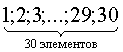
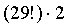
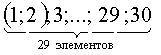
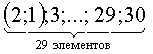
Если 1 и 2 тома должны стоять рядом, то число вариантов расстановки сокращается до , т.к. комбинацию из 1 и 2 тома можно считать за один том, но при этом они могут стоять как (1;2) или (2;1), т.е.

, .

Тогда искомое число способов расстановки есть

ПРИМЕР 13.2.10. Чемпионат, в котором участвуют 16 команд, проводится в два круга, т.е. каждая команда дважды встречается с любой другой. Определить, какое количество встреч следует провести.

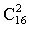
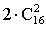
Решение: По условию задачи из 16 команд для каждой встречи требуется отобрать 2 команды. В данном случае отбор производится без повтора и порядок отбора не важен, т.е. число вариантов — . Так как команды должны играть дважды число вариантов удваивается, т.е. .

ПРИМЕР 13.2.11. Автомобильная мастерская имеет для окраски 10 основных цветов. Сколькими способами можно окрасить автомобиль, если смешивать от 3 до 7 основных цветов?

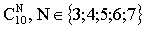
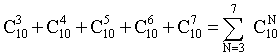
Решение: По условию задачи отбор цветов для окраски производится без повтора и порядок отбора не важен, т.е. число вариантов зависит лишь от числа отбираемых для окраски цветов — . Поэтому общее число вариантов есть

.

ПРИМЕР 13.2.12. Турист прошел маршрут из пункта A в пункт B, из B в C и вернулся обратно. Сколько вариантов маршрута существует, если из пункта A в пункт B ведут 3 дороги, а из B в C — 4 и нельзя возвращаться той дорогой, по которой уже прошел?

Решение: Составим схему.

Из рисунка видно, что вариантов маршрута из А в B существует 3, и из B в C – 4, т.е. всего маршрутов .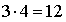

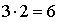
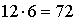
На обратном пути вариантов маршрута из С в B существует 3 (один уже пройден), и из B в А – 2, т.е. всего возможных обратных маршрутов осталось . Тогда всего вариантов маршрута .

ПРИМЕР 13.2.13. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда по 6 человек, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?

Решение: Рассуждения произведем несколькими способами

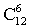
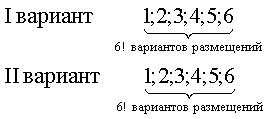
I способ) Первоначально 12 учеников разбивают на 2 группы по 6 человек. Это можно сделать способами.

Затем они могут распределиться по своим рядам согласно схеме

.

Поэтому всего способов распределения учеников будет .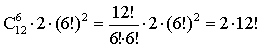

II способ) Первоначально 12 учеников запускают в класс, указывая место, где каждый должен сидеть, например “второй ряд, третье место”. Так как посадочных мест также 12, то всего вариантов распределения 12!
Варианты контрольной работы могут распределиться

“I вариант – I ряд, II вариант – II ряд”

“II вариант – I ряд, I вариант – II ряд”,

Таким образом, всего способов распределения учеников будет .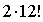

По приведенным решениям видно, что результаты решений совпадают.

ПРИМЕР 13.2.14. Сколько существует вариантов расположения шести гостей за круглым шестиместным столом?

Решение: Эта задача имеет разные решения и, соответственно разные ответы – в зависимости от того, что понимать под различным расположением гостей за столом. Поэтому исследуем возможные варианты.

Если считать, что нам важно, кто сидит на каком стуле, то это простая задача на перестановки и, следовательно, всего вариантов .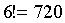

Если же важно не то, кто какой стул занял, а то, кто рядом с кем сидит, то требуется рассмотреть варианты взаимного расположения гостей. В таком случае, расположения гостей, получаемые одно из другого при повороте гостей вокруг стола, фактически являются одинаковыми (смотри рисунок).

Очевидно, что для любого расположения гостей таких одинаковых вариантов, получаемых друг из друга поворотом, — шесть. Тогда общее число вариантов уменьшается в шесть раз и их остается .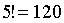
В случае же, когда нас интересует только взаимное расположение гостей, то одинаковыми можно считать и такие симметричные расположения, при которых у каждого гостя остаются те же соседи за столом, только левый и правый меняются местами (смотри рисунок).

В такой постановке вопроса общее число различных вариантов расположений гостей уменьшается вдвое и составляет 60.

Отметим, что каждое решение будет считаться правильным при соответствующей постановке задачи.

ПРИМЕР 13.2.15. Семнадцать студентов сдали экзамены по 4 предметам только на “хорошо” и “отлично”. Верно ли утверждение, что хотя бы у двух из них оценки по экзаменационным предметам совпадают?

Решение: Очевидно, что в данном случае речь идет о возможных вариантах вида

Предмет	1	2	3	4
Студент 1	4	4	5	5
Студент 2	5	4	4	5
Студент 3	5	5	5	5
…	…	…	…	…
Студент 17	4	4	5	4

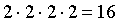
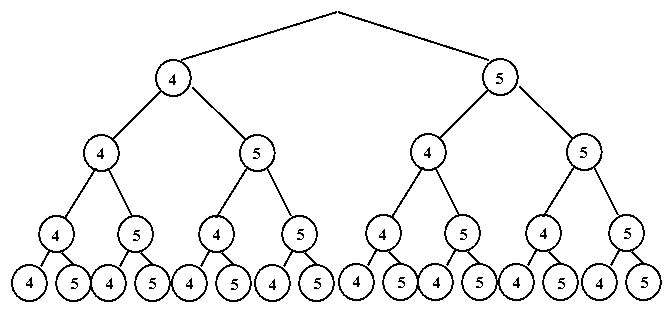
Данный пример можно решить способом, изложенным в примере 13.1.8., и получить количество вариантов . Приведем другой наглядный способ решения, использующий так называемое “дерево решений”,который представляет все варианты (16 штук) получения экзаменационных оценок.

.

По “дереву решений” видно, что 16 студентов могут сдать экзамены только на “хорошо” и “отлично” так, что их результаты будут отличаться, но если студентов 17, хотя бы одно повторение обязательно будет.

При решении задач комбинаторики используются следующие правила.

Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может быть выбран nспособами, то:

Правило суммы: выбрать либо A, либо B можно m+n способами.

Правило произведения. Пара объектов (A,B) в указанном порядке может быть выбрана 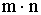способами.

Примеры и задачи для самостоятельного решения

Решить комбинаторную задачу.

13.2.1.1. В группе 25 студентов. Сколькими способами можно выбрать старосту, заместителя старосты и профорга?

13.2.1.2. В группе 25 студентов. Сколькими способами можно выбрать актив группы, состоящий из старосты, заместителя старосты и профорга?

13.2.1.3. Сколькими способами можно составить список из 10 человек?

13.2.1.4. Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой?

13.2.1.5. Буквы азбуки Морзе образуются как последовательности точек и тире. Сколько букв можно составить, используя для кодировки каждой из букв: а) ровно 5 символов? б) не более пяти символов?

13.2.1.6. Кости для игры в домино метятся двумя цифрами. Кости симметричны, и поэтому порядок чисел не существенен. Сколько различных костей можно образовать, используя числа 0,1,2,3,4,5,6?

13.2.1.7. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти различных звуков?

13.2.1.8. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?

13.2.1.9. В некоторых странах номера трамвайных маршрутов обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов?

13.2.1.10. Команда компьютера записывается в виде набора из восьми цифровых знаков – нулей и единиц. Каково максимальное количество различных команд?

13.2.1.11. Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы 1 и 2 находились бы в соседних аудиториях?

13.2.1.12. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?

13.2.1.13. Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной?

13.2.1.14. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?

13.2.1.15. У одного студента есть 7 DVD дисков, а у другого – 9 дисков. Сколькими способами они могут обменять 3 диска одного на 3 диска другого?

13.2.1.16. На вершину горы ведут 7 дорог. Сколькими способами турист может два раза подняться на гору и спуститься с нее, если по одной и той же дороге нельзя проходить дважды?

13.2.1.17. У ювелира было 9 разных драгоценных камней: сапфир, рубин, топаз и т.д. Ювелир планировал изготовить браслет для часов, однако три камня было украдено. Насколько меньше вариантов браслета он может изготовить по сравнению с первоначальными планами?

13.2.1.18. В поезд метро на начальной станции вошли 10 пассажиров. Сколькими способами могут выйти все пассажиры на последующих 6 станциях?

13.2.1.19. За одним столом надо рассадить 5 мальчиков и 5 девочек так, чтобы не было двух рядом сидящих мальчиков и двух рядом сидящих девочек. Сколькими способами это можно сделать?

13.2.1.20. В классе 25 учеников. Верно ли утверждение, что, по крайней мере, у трех из них день рождения в один и тот же месяц?

13.2.1.21. На участке железной дороги расположено 25 станций с билетной кассой в каждой. Касса каждой станции продает билеты до любой другой станции, притом в обоих направлениях. Сколько различных вариантов билетов можно выдать на этом участке?

13.2.1.22. На официальном приеме 50 человек обменялись рукопожатиями. Сколько было сделано рукопожатий?

13.2.1.23. Сколько диагоналей у выпуклого двадцатиугольника?

Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник